|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||
|
|||||||||||||||||||
|
|
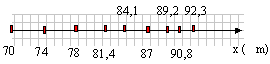
Un avion atterit sur le pont d'un porte-avions. Le pont est supposé plan et horizontal. Il est assimilable à un référentiel galiléen. Le freinage de l'avion est uniquement assuré par des câbles, solidaires du pont, qui s'accrochent à l'avion et le stoppent progressivement. Le mouvement de l'avion sur le pont peut être assimilé à un mouvement de translation rectiligne. On ne tiendra pas compte des forces de frottements. La masse de l'avion est m = 1,2 104 kg. On choisit comme instant initial t=0 , l'instant où l'avion touche le pont. Pour repérer la position de l'avion sur le pont, on mesure la coordonnée d'un de ses points sur un axe Ox, parallèle à la trajectoire, orienté dans le sens du mouvement et dont l'origine O se trouve à une extrémité du pont( celle où l'avion atterit). partie A : A la date t = 2s, une série de clichés de l'avion est prise à
intervalles de temps réguliers Dt=0,1 s.
Seul un point de l'avion a été représenté.
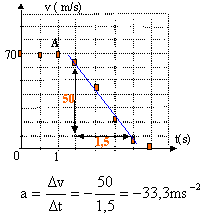
partie B : Des capteurs répartis sur tout le pont du porte-avions enregistrent la valeur de la vitesse instantanée v(t) de l'avion à partir de la date t=0 où il touche le pont. Le point A corespond à l'accrochage des câbles sous l'avion. 
vitesse (m/s) à t = 2,2 s = Dx / D t = (81,4-74) / 0,2 = 37 m/s
le mouvement est décéléré ( la vitesse diminue) ; le mouvement est rectiligne : vecteur vitesse et vecteur accélération sont colinéaires de sens contraire. l'avion est soumis à son poids, à l'action du support et à l'action F des câbles ( les frottements sont négligés) poids et action du support se neutralisent ;la 2ème loi de Newton s'écrit alors sur l'axe Ox : F = ma soit F= 1,2 104 (-40) = -4,8 105 N. cette force est colinéaire au vecteur accélération. à partir du théorème de l'énergie cinétique : entre les dates t = 2,1 s et t = 2,7 s vinitiale = 40 m/s donc Ec i = ½*1,2 104 * 40² = 9,6 106 J vfinale = 16 m/s donc Ec f = ½*1,2 104 * 16² = 1,536 106 J DEc = (1,536 -9,6)= -8,064 106 J poids et action du support, forces perpendiculaires à la vitesse, ne travaillent pas. travail de l'action des câbles : F *AB cos (180) = -F *AB avec AB= 90,8-74 =16,8 m la variation de l'énergie cinétique est égale à la somme des travaux des forces : -8,064 106 = - 16,8 F d'où la norme de
F : 4,8 105
N.
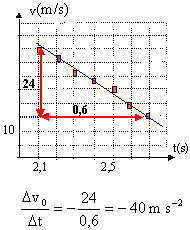
la trajectoire est une droite : le mouvement est rectiligne. la durée du parcours est voisine de 1 s (lecture graphe) et la norme de la vitesse vaut 70 m/s : la distance D parcourue est alors : D= 70*1 = 70 m. d'après le graphe v=f(t) : à t = 2,1 s la norme du vecteur vitesse vaut 40 m/s et entre t=2,1 s et t=2,7s le graphe est une fonction affine décroissante. ce qui est en accord avec les mesures de la partie A. calcul de la norme de F à la date t = 1,5 s. tracer la tangente à la courbe v=f(t) à t=1,5 s et déterminer son coefficient directeur.
appliquer la seconde loi de Newton : poids et action du sol se neutralisent (frottements négligés) . suivant un axe horizontal F = ma = 1,2 104 *(-33,3 ) = -4 105N. la norme de F vaut 4 105 N ; le vecteur F et le vecteur vitesse sont colinéaires et de sens contraire. |
||||||||||||||||||
|
 Le
premier point correspond à t = 2s, le second à t = 2,1 s ...
Le
premier point correspond à t = 2s, le second à t = 2,1 s ...