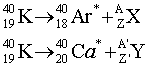Aurélie 06/02

datation par la méthode du potassium-argon

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


Certaines roches volcaniques contiennent du potassium ( symbole K) dont une partie est l'isotope 40( Z=19 ; A=40) qui se désintègre en calcium 40Ca et en un gaz inerte l'argon 40Ar (Z=18). La demi-vie du potassium 40 étant 1,25 109 ans, la datation sera basée sur la proportion, dans la roche, du potassium et de l'argon. Cette méthode permet de dater l'ensemble des 4,6 109 ans d'histoire de la terre.

Au moment de leur formation ces roches ne contiennent pas d'argon, puis le potassium 40 disparaît en même temps que l'argon apparaît. Pour dater la formation de cette roche, un géologue analyse un échantillon d'obsidienne et constate que les atomes d'argon y sont 2,5 fois moins nombreux que les atomes de potassium 40.

  1. Donner la composition des noyaux de potassium 40 et d'argon 40.
    - Ecrire les équations de réactions nucléaires possible, en précisant les lois de conservation utilisées qui permettent à partir du potassium 40 de former l'argon 40 d'une part et le calcium 40 ( Z=20) d'autre part.
  2. Cette roche contient 5% en masse de potassium. 0,012% est sous forme de potassium 40.
    - Calculer la constante radioactive l du potassium 40 en an-1 et en s-1.
    - Calculer l'activité d'un échantillon de masse m =100g.
    - Pour dater la formation de la roche, le géologue utilise le graphe ci-dessous donnant le rapport NAr / NK en fonction du temps. Déterminer l'age approximatif de la roche.

masse atomique du potassium 40 : M= 40g/mol ; N= 6,02 1023 mol-1.

 

.
.

corrigé
le noyau de potassium 40 compte : 19 protons ; 40 -19 = 21 neutrons.

le noyau d'argon 40 compte : 18 protons ; 40-18 = 22 neutrons.

le noyau de calcium 40 compte : 20 protons ; 40-20 = 20 neutrons.

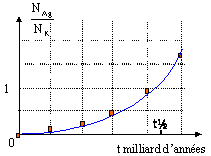
conservation de la charge : 19 = 18 + Z d'où Z =1

19 = 20 + Z ' d'où Z ' = -1

conservation du nombre de nucléons : 40 = 40 + A d'où A=0

40 = 40 +A' d'où A' = 0

la particule 10X est un positon, la particule -10Y est un électron

constante radioactive : t½ l = ln 2 ou bien l = ln 2 / t½

l = ln 2 / 1,25 109 = 5,545 10-10 ans -1.

1 an = 365*24*3600 = 3,154 107 s ; t½ =1,25 109 * 3,154 107 = 3,94 1016 s.

l = ln 2 / 3,94 1016 = 1,76 10-17 s -1.

activité : nombre de désintégrations par seconde

masse de potassium dans 100 g : 5g ; masse de potassium 40 : 5*1,2 10-4 =6 10-4 g

soit masse (g) / masse molaire (g/mol) = 6 10-4 / 40 = 1,5 10-5 mol

1,5 10-5 * 6,02 1023 = 9,03 1018 noyaux de potassium 40

activité : 9,03 1018*1,76 10-17 = 159 Bq.

date approximative :

les atomes d'argon sont 2,5 fois moins nombreux que les atomes de potassium : NAr / NK = 1/2,5 = 0,4.

lecture graphe : t voisin de 6 108 ans.

par le calcul :

au départ à t=0, N0 noyaux de potassium et aucun noyau d'argon.

nombre de noyaux de potassium 40 à la date t : NK=N0e-lt soit N0/ NK= elt

nombre de noyaux d'argon à la date t : NA=N0-NK

NA / NK = (N0-NK) / NK = N0/NK-1

N0/NK = NA / NK +1 = 0,4+1 = 1,4.

1,4 = elt avec l= ln2 / t½

ln 1,4 =lt = ln2 * t / t½

t = t½ * ln 1,4 / ln2 = 1,25 109 *0,336 / 0,693 = 0,6 109 ans.

 

à suivre ...
retour - menu
à bientôt ...