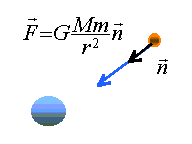Extraits de l'ouvrage de Newton "Les principes mathématiques de la philosophie naturelle", d'après la traduction de Mme de Chastelet (1756-1759).

Extraits du livre I :

Proposition I : les forces par lesquelles les satellites de Jupiter sont retirés perpétuellement du mouvement rectiligne (...), sont dirigées vers le centre de Jupiter et sont inversement proportionnelles aux carrés de leur distance à ce centre.

Proposition V : les satellites de Jupiter gravitent vers Jupiter, ceux de Saturne vers Saturne, et les planètes principales vers le Soleil, et c'est par la force de leur gravité que ces corps (...) sont retirés à tout moment de la ligne droite et qu'ils sont retenus dans des orbites curvilignes.

Proposition VI : tous les corps gravitent vers chaque planète et, sur la même planète, (...) leurs forces de gravité, à égale distance du centre, sont proportionnelles à la masse que chacun d'eux contient.

On considère que tous les satellites et planètes sont des corps dont la répartition de la masse est à symétrie sphérique. Les mouvements sont étudiés dans le référentiel "jupitérocentrique" (d'origine le centre de Jupiter et d'axes dirigés vers trois étoiles fixes). On note M la masse de Jupiter et G la constante de gravitation universelle.

1. On étudie le champ de gravitation de Jupiter.
   - Donner l'expression vectorielle de la force d'interaction gravitationnelle exercée par Jupiter sur un de ses satellites de masse m et situé à la distance r du centre O de Jupiter. Faire un schéma explicatif.
   - Donner, dans les propositions ci-dessus extraites du livre I, les citations en accord avec cette expression vectorielle.
   - Donner l'expression vectorielle du champ de gravitation créé par Jupiter, à la distance r de son centre.
   - Représenter quelques lignes du champ de gravitation autour de Jupiter.
   - Pourquoi est-il important de préciser que la répartition de la masse des corps est à symétrie sphérique ?
2. On considère que Ganymède, un satellite de Jupiter, satellite de masse m, est soumis à la seule force de gravitation due à Jupiter et que son mouvement est circulaire de centre O (centre de Jupiter) et de rayon r.
   - Montrer que le mouvement du satellite est uniforme.
   - Etablir l'expression de la vitesse v de Ganymède en fonction de G, M et r ; en déduire l'expression de la période T de révolution.
   - Parmi les plus gros satellites de Jupiter, Europe gravite à raison de 14 km par seconde alors que Ganymède met 1 minute pour parcourir 660 km. Quel est le satellite le plus éloigné de Jupiter ? Justifier.
3. On considère que Ganymède se déplace sur son orbite de A en C en 1 seconde (voir figure 1) et que le rayon r de cette orbite est de l'ordre de un million de kilomètres.
   
   - D'après les extraits cités, que représente la droite AB sur la figure 1 ?
   - Si a (en radian) est très petit, BC est égal à ½r a². En déduire que BC est aussi égal à ( arc (AC))² / (2r), où arc (AC) représente l'arc de cercle entre A et C. Vérifier que la distance BC vaut environ 6 cm.
   - Supposons qu'on laisse tomber une pierre de l'altitude de Ganymède en direction de Jupiter. On admet que la hauteur de chute, pendant la première seconde, se calcule par l'expression ½Gt², G représentant la valeur du champ de gravitation à cette altitude, soit G = 0,12 m.s^-2. Calculer la hauteur de chute durant la première seconde.
   - Compte tenu des résultats des questions 3.2 et 3.3 et des propositions de Newton, que représente BC pour Ganymède ?

---

. .

---

corrigé

---

Les citations concernées sont :

"Les forces [...] sont dirigées vers le centre de Jupiter et sont inversement proportionnelles au carré de leur distance à ce centre."

"leurs forces de gravité, à égale distance du centre, sont proportionnelles à la masse que chacun d'eux contient."

Le champ de gravitation créé par Jupiter en S est :

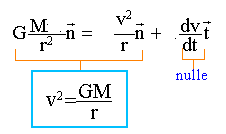
Les lignes de champ sont radiales, orientées vers le centre O de Jupiter.

Si la répartition de la masse des corps est à symétrie sphérique, on peut alors considérer que toute la masse du corps est concentrée en son centre : condition d'application de la formule de Newton

La dérivée de la norme du vecteur vitesse par rapport au temps étant nulle, alors la norme de la vitesse est constante et le mouvement est uniforme.

La vitesse du satellite est indépendante de sa masse, est d'autant plus grande que le rayon de l'orbite est petite.( le plus proche de Jupiter) .

période : durée pour décrire la circonférence à la vitesse v, norme constante.

2pr = vT

élever au carré, puis remplacer v² par l'expression ci dessus.

4p² r² =GM / r T²

ou T² =4p² /(GM) r³. ( 3 ème loi de Kepler)

En 60s , Europe parcourt 14*60 = 840 km alors que Ganymède ne parcourt que . Plus r est grand, plus v est petit, c'est donc Ganymède qui gravite le plus loin des deux de Jupiter.

---

D'après les extraits cités, la droite AB représente la trajectoire de laquelle les satellites sont retirés à tout moment par la force de leur gravité.

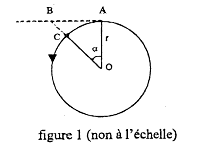
Par définition arc (CA) = r a d'où a ² = ( arc (CA))² / r²

or BC = ½ ra² donc BC =½ r( arc (CA))² / r² = ( arc (CA))² / (2r).

Pour Ganymède : V = 660 / 60 = 11 km/s donc arc (CA) = 11 km = 1,1 10⁴ m.

BC = (1,1 10⁴)² / (2 10⁹) = 1,21 10⁸ / 2 10⁹ = 0,121 / 2 = 0,06 m = 6 cm.

Cette hauteur de chute en est : h =½Gt²

h= 0,5*0,012 + 1² = 0,06 m = 6cm.

Comme on trouve 6 cm, on peut dire que BC représente la hauteur de chute de Ganymède en 1 seconde.