|
sportifs de haut niveau 09/96 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||
|
||||||
|
|
étude d'un texte historique "J'ai pris deux balles, l'une de plomb, l'autre de liège, celle-là bien plus de cent fois plus lourde que celle-ci ,toutes deux attachées à des fils fins et égaux, longs de 4 à 5 coudées(la coudée est une ancienne mesure de longueur,équivalant à la distance du coude au bout du médius ,soit environ 50 centimètre), fixés par le haut .Puis ,les ayant éloignées l'une et l'autre de la verticale, je les ai laisées aller en même temps;et toutes deux descendant le long des circonférences des cercles décrits par les fils et de rayons égaux,dépassèrent la verticale;puis elles revinrent en arrière par le même chemin et répétant bien cent fois les mêmes allées et venues,elles ont montré d'une manière évidente que le boule lourde marche tellement dans le même temps que la légère ,qu'elle ne dépasse pas ce temps ni cent oscillations, ni en mille du plus petit intervalle ,mais elle marche d'un pas tout à fait égal. Éloignant le pendule de plomb à 50° de la verticale, et le laissant en liberté, il court, et dépassant la verticale presque de 50 autres degrés, il décrit un arc de près de 100° .retour - menunant alors en arrière sur lui-même, il décrit un autre arc plus petit : et continuant ses oscillations, après un grand nombre de celles-ci, il revient enfin au repos. Chacune de ces oscillations se fait dans des temps égaux, tant celle de 90° , que celle de 50° ou de 20°, de 10°, de 4° .Il s'ensuit que la rapidité du mobile diminue toujours, puisque dans des temps égaux il décrit successivement des arcs de plus en plus petits. Ensuite, quant à la proportion des temps des oscillations des mobiles suspendus à des fils de différentes longueurs, des expériences répétées, des chacun peut faire m'ont démontré que ces temps sont en proportion sous-doublée des longueurs des fils; en d'autres termes, les longueurs des fils sont en proportion doublée des temps, c'est-à-dire qu'elles sont comme les carrées des temps des oscillations isolées ou d'un égal nombre d'oscillations; de sorte que ,si l'on veut que le temps des oscillations d'un pendule soit double du temps des oscillations d'un autre, il faut que la longueur de la corde de celui-là soit quadruple de la longueur de la corde de celui-ci .Et alors dans le temps d'une vibration d'un pendule, un autre en fera trois, si sa corde est neuf fois moins longue que celle de l'autre. Il suit de là que les longueurs des cordes ont entre elles la proportion réciproque qu'ont les carrées des nombres des oscillations qui se font dans le même temps" (traduction de j.Gay d'extraits des dialogues de Galilée,publiés en 1632) d'après "physique et physiciens" Robert Massain ed. Magnard questions :
exercice 2 : Pour permettre d'apporter une preuve expérimentale, élégante et simple de la rotation de la Terre sur elle-même, Foucault imagina plusieurs expériences qui utilisent les propriétés d'un pendule simple. Celle réalisée au Panthéon eut un grand succès populaire. Il fit connaître sa découverte à l'académie en 1851 : voici des extraits du texte de sa communication: "Le mouvement de la Terre sur elle-même est ici rendu évident au moyen d'un grand pendule, dont le fil attaché au sommet de la coupole descend jusqu'au niveau de la rampe et porte à son extrémité inférieure une boule formée d'une enveloppe de cuivre renfermant une masse de plomb qui la remplit complètement. Le fil a 67 mètres long ...;la boule pèse 28 kilogrammes... Quand il est au repos, le pendule marque le point de centre commun à la table et au grand cercle de bois (la rampe) qui l'entoure.Ce cercle a 6 mètres de diamètre.." "Si (...)on éloigne de sa position d'équilibre la masse du pendule et si on l'abandonne à l'action de la pesanteur sans lui communiquer aucune impulsion latérale, son centre de gravité repassera par la verticale, et, en vertu de la vitesse acquise, il s'élèvera de l'autre côté de la verticale à une hauteur presque égale à celle d'où il est parti. Parvenu à ce point, sa vitesse expire, change de signe, et le ramène, en le faisant encore passer par la verticale, un peu au dessous de son point de départ.Ainsi l'on provoque un mouvement oscillatoire de la masse pendulaire suivant un arc de cercle dont le plan est nettement déterminé et auquel l'inertie de la masse assure une position invariable dans l'espace." "Ce pendule, le plus grand qui ait été construit jusqu'ici, donne une oscillation de huit secondes; il lui faut 16 s pour aller et venir. Quoique ces oscillations diminuent d'amplitude assez rapidement, au bout de cinq ou six heures, elles sont encore assez grandes. "Pour lancer le pendule on écarte la "boule" jusqu'au bord du grand cercle en bois et on lâche sans vitesse initiale" et, pour voir comment il marche, on place sur le rebord du cercle de bois deux bancs (tas) de sable humide, fraîchement moulés lis sont alignés selon la course du pendule. Celui-ci pratique en passant sur chacun d'eux, une petite brèche qui s'agrandit de plus en plus tant que oscillations dépassent le cercle de bois. L'agrandissement de la brèche a toujours lieu vers la gauche de la personne qui regarde vers le centre, comme si le plan d'oscillation tournait de droite à gauche..." (dans toutes les expressions littérales on notera L la longueur du fil , m la masse de la "boule" , pour les applications numériques, on prendra g=9,81 m.s-2. questions : Lorsque l'angle a est petit, il est recommandé d'utiliser les formules d'approximation suivantes: a ( rad) voisin tan a voisin sin a cos a =1 - a²/2 (l'angle s'exprime en radian)
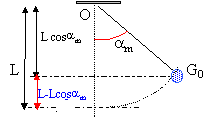
étude énergétique : Le pendule est écarté de sa position de repos de l'angle am et lâché sans vitesse initiale. L'énergie potentielle du système pendule-terre est choisie égale à zéro pour la position de repos du pendule.
expérience de Foucault :
On a pris deux boules de masses m différentes qu'on a suspendu par un fil de longueur L, a un point fixe, et on les a écartés d'un angle a ; puis on les a lâché sans vitesse initiale afin d'observer leur mouvements. Cette expérience est le principe du pendule simple. La période d'un pendule simple ne dépend pas de la masse des boules accrochées à l'extrémité du fil.Le résultat de cette expérience est en accord avec l'expression de la période du pendule simple, car la période T0 d'un pendule simple vaut : T0=2p racine carrée (L / g) dans cette expression la masse ne figure pas.
On les qualifie d'oscillations amorties. si
l'amortissement est faible la durée d'une oscillation est appelé "
pseudo période "
la période est proportionnelle à la racine carrée de la longueur du pendule.
longueur de l'arc de cercle : 6 m, rayon du cercle 67 m : rayon du cercle (m) fois 2a ( radian)= longueur arc de cercle (m) 2a ( radian) = 6 / 67 =0,089 rad soit 0,089*180/3,14 = 5,2 °. soit a m = 2,6°. le mot " demi -période " doit être employé à la place du mot "oscillation" La période mesurée vaut 16 s. T0=2p racine carrée (L / g) L'intensité de pesanteur s'exprime en m.s -2 ; sa dimension est donc [L] . [T] -2 . La longueur du fil s'exprime en mètres, sa dimension est donc [L]. (L/g ) a la dimension d'un temps au carré. T0 a la dimension d'un temps. T0 = 2*3,14 racine carrée ( 67 /9,8) = 16,4 s. (16,4-16) / 16 =
2.5% ,la période du pendule de Foucault est proche de celle d'un
pendule simple. La différence est surtout due à l'incertitude sur la
longueur.
Le système S possède de l'énergie cinétique Ec et de l'énergie de potentielle de pesanteur Ep. Energie du système S a l'instant initial : Comme on lâche le pendule sans vitesse initiale, son énergie cinétique Ec est nulle. Il possède de l'énergie potentielle de pesanteur uniquement. Em = Ep = mgh = mg OH = mgL ( l - cos am)
Em= 28*9,81*67* ( l -cos 2,6) = 18,9 J. Hypothèse: On considère que sur ce trajet les frottements sont négligeables et que l'énergie mécanique du système S = { pendule , Terre}est constante. Au point O, la vitesse du pendule est maximale car l'énergie potentielle de pesanteur du système S est minimale ( l'énergie potentielle est nulle au point O car l'énergie potentielle du système S = { pendule - Terre} est choisie égale à zéro pour une position de repos du pendule). Em = Ec + Ep = ½mv0² v0 = racine carrée (18,9*2 / 28) = 1,16 m/s. A l'instant t =
0s , le système S ne possède que de l'énergie potentielle de pesanteur.
Au cours du mouvement cette énergie potentielle de pesanteur diminue
jusqu'à la position d'équilibre tandis que l'énergie cinétique
augmente. Lorsque le pendule remonte, l'énergie cinétique diminue
jusqu'à s'annuler et l'énergie potentielle augmente jusqu'à sa valeur
maximale.
La période du pendule simple ne dépendant pas de la masse, celle-ci n'est pas modifiée. Seule la masse du pendule a changé. L'énergie mécanique initiale est proportionnelle a la masse du pendule. L'énergie mécanique initiale est plus grande car on remplace une boule de 28 kg par une boule de 47 kg. Le plan d'oscillation devrait être fixe, or on s'aperçoit que le plan d'oscillation tourne : " le plan est nettement déterminé et auquel l'inertie de la masse assure une position invariable dans l'espace ", " le pan d'oscillation tournait de droite a gauche ". Foucault observe une rotation du plan d'oscillation du pendule attribuée a la rotation de la terre.
|
|||||
| |
||||||
|