Aurélie 03/02

dipôle RLC série régime libre

La réunion 07/00

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.


analyse du fonctionnement du montage : on note R la résistance totale de la maille KABM.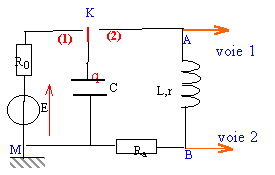

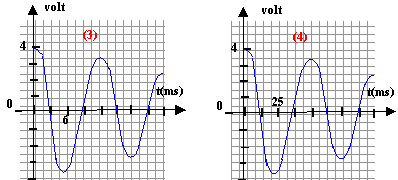
  1. Quel est le rôle de l'interrupteur K ?
  2. Aux bornes de quels dipôles sont prélevées les tensions appliquées aux voies 1 et 2. Les nommer ( exemple Uxy).
  3. A défaut d'une interface d'acquisition pour l'ordinateur, quel type d'appareil peut-on utiliser pour réaliser les enregistrements reproduits figures 2, 3,4 ci-dessous ? Justifier.

Exploitations d'enregistrements : C= 20mF et L= 0,8 H et E = 4V , r = Ra = 10 ohms)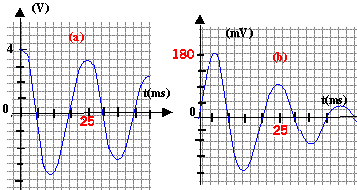

 
  1. Identifier les courbes (a) et (b) en leur attribuant les tensions définies à la question précédente. Justifier.
  2. Déterminer graphiquement la pseudopériode T2 des oscillations.
  3. Calculer l'énergie totale du circuit à l'instant t=0 ( l'origine des temps coîncide avec le début de la décharge du condensateur).
  4. Soit t1, la date à laquelle la tension aux bornes de la résistance passe par son premier maximum.
    - Déterminer l'intensité du courant à cette date et en déduire l'énergie stockée dans la bobine à la date t1.
    - Est-ce la seule forme d'énergie stockée à la date t1. Justifier.
    - Exprimer l'énergie stockée à la date t1 en pourcentage de l'énergie totale initiale.
    - On souhaite augmenter ce pourcentage. Sur quel paramètre doit-on agir? Justifier.

pseudo-période et période propre :

  1. Déterminer graphiquement les pseudo-période T3 et T4 des oscillations reproduites ci-dessous.

    - Reproduire et compléter le tableau suivant :
    figure
    C(mF)
    L(H)
    T pseudo-période (ms)
    A= T ² / (LC)
    a
    20
    0,8

    3
    20
    0,2

    4
    80
    0,8

    - Que peut-on dire de A pour ces trois expériences ?

  2. L'intensité du courant vérifie l'équation différentielle : i" + R/L i' + 1/ (LC) i = 0.
    - Quelle forme prendrait cette équation si les oscillations libres n'étaient pas amorties ?Justifier
    - En déduire l'expression littérale de la période T0 des oscillations en fonction des nouvelles caractéristiques du circuit. En déduire la valeur de A0 = T²0 / (LC).
.
.

corrigé
interrupteur K :

en position (1) l'interrupteur ferme le circuit comprenant en série une résistance R0, un condensateur C et un générateur de tension continue : le condensateur se charge et stocke l'énergie ½ CE².

en position (2) cet interrupteur relie le condensateur précédemment chargé à une bobine inductive : décharge du condensateur à travers la bobine inductive.

sur la voie 1 on visualise la tension UAM aux bornes du condensateur.

sur la voie 2 on visualise la tension UBM aux bornes du résistor Ra, image de l'intensité.

A défaut d'un interface et d'un ordinateur on peut utiliser un oscilloscope.

La courbe (a) correspond à la tension UAM aux bornes du condensateur : à t = 0 le condensateur est chargé et la tension UAM est maximale égale à E soit 4 V.

La courbe (b) correspond la tension UBM aux bornes du résistor Ra, image de l'intensité : à t = 0 l'intensité est nulle dans le circuit.

à t = 0 énergie stockée dans le condensateur : ½CE² = 0,5 * 20 10-6 *4² = 1,6 10-4 J.

la bobine ne stocke pas d'énergie car l'intensité est nulle à t=0.

à la date t1, la tension UBM aux bornes du résistor Ra vaut 0,18 V et Ra = 10 ohms

en conséquence i = 0,18 /10 = 0,018 A

la tension aux bornes du condensateur est nulle à la date t1 : ce dernier ne stocke pas d'énergie.

énergie stockée dans la bobine : ½Li² = 0,5*0,8*0,018² = 1,3 10-4 J.

soit en pourcentage : 1,3 / 1,6 *100 = 81 %.

pour augmenter ce pourcentage il faut diminuer les pertes d'énergie due à la résistance du circuit : par exemple diminuer ou annuler la valeur de Ra.

T3 = 12 ms = 0,012 s et T4 = 50 ms = 0,05 s (lecture graphes (3) et (4) respectivement.)

figure
C(mF)
L(H)
T pseudo-période (ms)
A= T ² / (LC)
a
20
0,8
25
39
3
20
0,2
12
36
4
80
0,8
50
39
les valeurs de A sont à peu près constantes voisines mais inférieures à 4 p².

équation différentielle si la résistance du circuit est nulle : i"+ 1/(LC) i =0

w² = 1 / (LC)

fréquence : f = w / (2p)

période T0 = 1/ f = 2p racine carrée (LC).

élever au carré T²0 = 4p² LC

A0= T²0 /(LC) = 4p² = 39,5.



à suivre ...
retour - menu
à bientôt ...