Aurélie 03/02

détermination expérimentale d'une inductance

Antilles 06/01

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


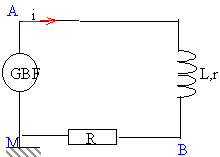
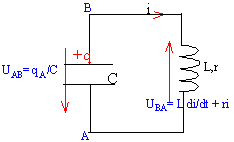
La bobine considérée est résistive ( résistance r) et inductive (inductance L).

  1. A l'aide d'un générateur de tension continue on alimente la bobine puis on insére des multimètres dans le circuit afin de mesurer l'intensité du courant qui la traverse et la tension aux bornes du générateur. La résistance de la bobine a été trouvée égale à 10 W. Expliquer briévement comment on a pu déterminer espérimentalement cette valeur à partir du montage proposé.
  2. Un générateur basse fréquence délivrant une tension en crénaux (0 V pendant une ½ période et 4 V pendant l'autre demi période ; f = 200 Hz) alimente la bobine (r, L) associée en série avec un conducteur ohmiquz de résistance R= 420 W.

    Un dispositif d'acquisition des données relié à un ordinateur prmet de suivre l'évolution en fonction du temps de l'intensité i du courant qui traverse la bobine. L'enregistrement correspond à la demi période pendant laquelle la tension aux bornes du générateur est 4V.

    - Quel élément du circuit est responsable du retard à l'établissement du courant ?
    - Quel phénomène physique est responsable de ce retard ?
    - Mesurer la constante de temps du circuit en utilisant le graphe.
    - Déterminer l'inductance L sachant que la constante de temps vaut L/ (R+r)

  3. Un condensateur de capacité C=0,25 mF est chargé à l'aide d'un générateur de tension de force électromotrice E= 6V puis déconnecté du générateur. A la date t=0, le condensateur chargé est relié à la bobine précédente.

    L'évolution de la tension UBA au cours du temps est enregistrée à l'aide de l'ordinateur.

    - Comment appelle-t-on ce type d'oscillations ?
    - Comment interpreter la décroissance de l'amplitude ?
    - Etablir l'équation différentielle à laquelle satisfait la tension UBA en respectant l'orientation de l'intensité.
    - Mesurer la pseudopériode T' des oscillations

  4. On considére que la résistance de la bobine est nulle.
    - Ecrire la nouvelle expression de l'équation différentielle à laquelle satisfait UBA.
    - Quelle est l'espression de la période des oscillations.
    - Calculer la valeur de l'inductance de la bobine en admettant que la pseudo période est identique à la période.

 

.
.

corrigé
résistance de la bobine :

tension aux bornes de la bobine : u = Ldi/dt + ri

en courant continu, lorsque le régime permanent est établit l'intensité est constante et en conséquence di/ dt = 0

par suite la tension aux bornes du générateur est égale à la tension aux bornes de la bobine u = ri

il suffit de mesurer l'intensité et la tension aux bornes de la bobine pour trouver r.

la bobine est responsable du retard à l'établissement du courant : celle ci stocke de l'énergie ( ½Li²) ce qui explique ce retard

il s'agit du phénomène d'auto-induction

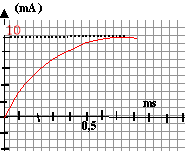
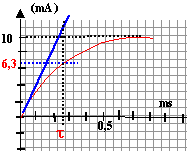
La constante de temps est la durée au bout de laquelle l'intensité atteint 63% de sa valeur maximale.

On peut aussi tracer la tangente à l'origine du graphe ci-dessus : le coefficient directeur de la tangente est : 10 / t.le graphe indique t voisin de 0,25 ms = 2,5 10-4 s.

calcul de L :

exprimer la constante de temps en seconde : 2,5 10-4 s.

R+r = 420+10 = 430 ohms

L = 430 * 2,5 10-4 = 0,107 H.

circuit RLC libre :

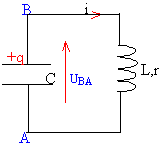
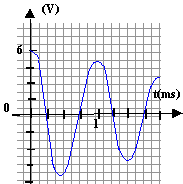
oscillations libres dans un dipole RLC, avec amortissement moyen : régime pseudopériodique.

la résistance du circuit est responsable de la diminution de l'amplitude des oscillations.

avec qA= -q et i = dqA / dt = -dq/dt = -q' soit di /dt = -q"

UAB + UBA = 0

-q/C + Ldi/dt +ri =0

-q/C -Lq" -rq' =0

q" + r/L q' + 1/(LC) q=0. ( équation différentielle pour la charge)

ou bien encore : UAB + UBA = 0

UAB + Ldi/dt +ri =0

q = CUBA ; i = dqA / dt = -CdUBA/dt = -CU'BA soit di /dt = -CU"BA

-UBA + Ldi/dt +ri =0

-UBA -LCU"BA -rCU'BA=0

U"BA+ r / L U'BA + 1/(LC)UBA =0

( équation différentielle pour la tension UBA )

mesure de la pseudo période sur le graphe : T' voisin de 1 ms = 10-3 s.

équation différentielle pour la tension UBA U"BA+ 1/(LC)UBA =0

w² = 1 / (LC)

fréquence : f = w / (2p)

période T0 = 1/ f = 2p racine carrée (LC).

élever au carré T²0 = 4p² LC

L = T²0 /(4p² C) avec C = 0,25 10-6 F ; T²0 = 10-6 s²

L = 10-6 / (4*3,14²*0,25 10-6 ) = 0,1 H.



à suivre ...
retour - menu
à bientôt ...