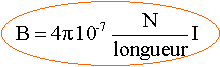Aurélie nov 2001

étude d'une bobine

Amérique du Nord 06/01

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


On dispose d'un solénoïde à double enroulement dont la fiche porte les indications suivantes :

enroulement 1 : N1 = 200 spires ; enroulement 2 : N2 = 400 spires ; longueur : L=40 cm ; Imax =5A ; les deux enroulements occupent la même longueur.

champ magnétique au centre du solénoïde :

On réalise le spectre magnétique du solénoïde lorsqu'il est parcouru par un courant d'intensité constante I.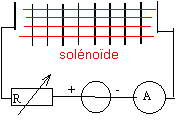

 

  1. Préciser la nature des faces du solénoïde. Justifier.
    - Quel est le nom donné au différentes lignes qui constituent l'empreinte magnétique.
    - Orienter ces lignes à l'intérieur du solénoïde.
    - Quelle est la propriété du champ magnétique à l'intérieur de la bobine.
  2. Le rhéostat permet de faire varier l'intensité I du courant dans le solénoïde. Un teslamètre permet de mesurer la valeur B du champ magnétique au centre de la bobine.
    I(A)
    0,5
    1
    1,5
    2
    2,5
    3
    3,5
    4
    B(mT)
    0,31
    0,6
    0,91
    1,21
    1,52
    1,84
    2,13
    2,44

    - Tracer le graphe B= f(I).
    - Montrer à partir de ce graphe que la relation liant B à I est de la forme kI. Déterminer numériquement k.
    - Quel enroulement a t-on utilisé pour réaliser cette étude.
    - Déduire de l'expression théorique donnant le champ à l'intérieur de la bobine, la valeur de B si I= 4,5 A

inductance de la bobine :

On se propose de déterminer l'inductance de la bobine par deux méthodes différentes :

  1. expérience 1 : dipole RL
    Le solénoïde d'inductance L et de résistance r =11 W est associé à un résistor R'=100 W. Soit R= R'+ r la résistance totale du dipole(RL).

    A la fermeture du circuit le dipole (RL) est soumis à un échelon de tension. On désire suivre l'évolution de l'intensité i en fonction du temps à l'aide d'un oscilloscope à mémoire.
    - Indiquer les branchements de l'oscilloscope permettant de visualiser i = f(t) et justifier.
    - On obtient la courbe suivante :

    Nommer le phénomène responsable du retard à l'établissement du courant dans le circuit. Quel est l'élément du circuit responsable de ce phénomène.
    - Déterminer graphiquement la constante de temps du circuit.
    - Cette constante de temps étant égale à L/ R , en déduire l'inductance de la bobine.

  2. expérience 2 : dipole RC :
    La bobine précédente est associée en série avec un condensateur de capacité C= 10mF, condensateur préalablement chargé. On enregistre à l'oscilloscope les variations de la tension aux bornes du condensateur en fonction du temps à la fermeture du circuit.

    - Ces oscillations sont-elles libres ou forcées. Justifier.
    - Pourquoi sont-elles amorties ?
    - Quelle est la pseudo-période des oscillations électriques ?
    - En déduire l'inductance de la bobine.

 

.
.

corrigé


champ magnétique :

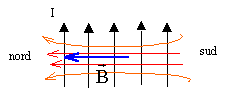
la règle de l'observateur d'Ampère permet de trouver le sens du champ magnétique connaissant le sens du courant.

L'ensemble des lignes de champ constituent le spectre magnétique :

le vecteur champ magnétique est tangent, en chaque point, aux lignes de champ.

Ces lignes sortent par la face nord de la bobine et rentrent par la face sud.

A l'intérieur de la bobine ( exceptions faites des extrémités) les lignes de champ sont parallèles : le champ est uniforme.

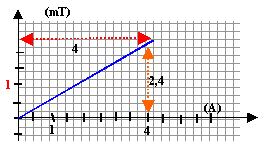
le graphe étant une droite, le champ magnétique et l'intensité sont proportionnels :

le coefficient de proportionnalité est : 2,4 10-3 / 4 = 6 10-4 T A-1. (tesla / ampère)

N= B longueur / (4p 10-7 I)

avec I=4 A ; B= 2,44 10-3 T et longueur = 0,4 m.

N = 2,44 10-3 *0,4 / (4*3,14 10-7 *4) voisin 200 spires.

valeur de B si I= 4,5 A :

B= 4*3,14 10-7 *200 /0,4 *4,5 = 2,82 10-3 T = 2,82 mT. 

dipole (RL) :

 

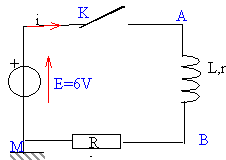
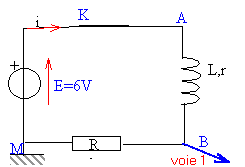
Aux bornes d'une résistance la tension est proportionnelle à l'intensité.

Visualiser cette tension c'est obtenir l'image de l'intensité au facteur R près.

pour visualiser la tension UBM, M est relié à la masse de l'oscilloscope et B est relié à l'une des entrées.

Le phénomène d'induction se produisant dans la bobine inductive provoque un retard à l'établissement du courant.

Pendant ce retard, la bobine stocke de l'énergie.

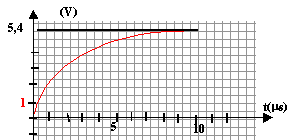
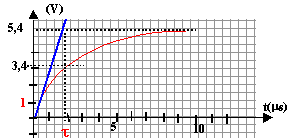
tracer la tangente à la courbe à la date t=0 :

cette tangente coupe l'asymptote horizontale à la date t = 2 ms.

à la date t = t la tension aux bornes du résistor est ègale à 63% de sa valeur finale soit 5,4 *0,63 = 3,4 V

tracer une droite horizontale passant par U = 3,4 V, l'intersection avec la courbe donne par lecture sur l'axe des temps la valeur de la constante de temps.

t = 2 10-6 s et R = 11+100 = 111 W.

2 10-6 = L / 111 d'où L = 2 10-6 *111 = 2,22 10-4 H = 0,22 mH.

dipole (RC) :

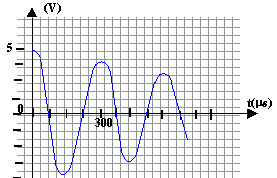
Les oscillations sont libres ( aucun générateur n'est monté en série avec le dipole RC)

les oscillations s'amortissent : au cours des échanges d'énergie entre bobine et condensateur, une petite partie de l'énergie est perdue par effet joule (chaleur) dans la résistance r de la bobine.

le graphe donne la période : T= 300 m s = 3 10-4 s

élever au carré

LC = T² / (4p²) d'où L = T² / (4p²C)

L = 9 10-8 / (4*3,14² 10-5 ) = 2,28 10-4 H = 0,228 mH.

à suivre ...
retour - menu
à bientôt ...