Aurélie nov 2001

masse de Jupiter

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


On se propose de déterminer la masse de Jupiter en étudiant le mouvement de ses principaux satellites : io ,Europe, Ganymède et Callisto

  1. Le mouvement d'un satellite, de masse m est étudié dans un référentiel considéré comme galiléen ,ayant son origine au centre de Jupiter et ses axes dirigés vers des étoiles lointaines, considérées comme fixes .On supposera que Jupiter et ses satellites ont une répartition de masse à symétrie sphérique. Le satellite se déplace sur une orbite circulaire, à la distance R du centre de Jupiter :
    - Déterminer la nature du mouvement d'un satellite autour de Jupiter .
    - Déterminer la vitesse v d'un satellite en fonction de R, de M, masse de Jupiter et de G, constante de gravitation universelle.
    - En déduire l'expression de la période de révolution T du satellite.
    - Montrer que le rapport T²/ R3 est constant.
  2. Les périodes de révolution et les rayons des orbites des quatre principaux satellites de Jupiter ont été déterminés et ont les valeurs suivantes :

    io
    Europe
    Ganymède
    Callisto
    T(en heures)
    42,5
    85,2
    171,7
    400,5
    R(en km)
    4,22 105
    6,71 105
    1,07 106
    1,883 106

    - Représenter sur papier millimétré le graphe donnant les variation de T² en fonction de R3. Conclure .
    - En reliant ces résultats à ceux obtenu ci-dessus, déterminer la masse M de Jupiter

donnée : G = 6,67 fois 10-11N.m2.kg-2. 

...

corrigé

le satellite est soumis à la seule force de gravitation centripète

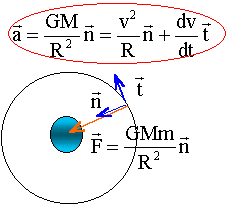
dans la base de Frenet :

suivant l'axe n = GMm /R² = mv²/ (R+h)

d'où la vitesse : v² =GM / R

suivant l'axe t : dv/dt = 0 doù norme de la vitesse constante et mouvement uniforme.

la circonférence du cercle 2pR est parcourue à la vitesse v pendant la durée T (période

2pR =vT

élever au carré et remplacer v² par son expression

4p²R²= GM / R T²

soit T² / R3 = 4p²/(GM) 3ème loi de Képler.

 

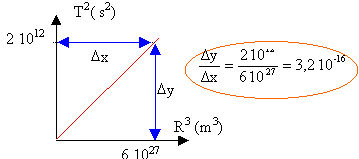
T² en fonction de (R+h) au cube donne une droite dont le coefficient directeur est 4pi²/GM


io
Europe
Ganymède
Callisto
T(en secondes)
1,53 105
3,07 105
6,18 105
1,44 106
R(en m)
4,22 108
6,71 108
1,07 109
1,883 109
T² en s²
2,34 1010
9,42 1010
3,81 1011
2,07 1012
R3 en m3
7,51 1025
3 1026
1,22 1027
6,64 1027
T² / R3
3,1 10-16
3,14 10-16
3,12 10-16
3,2 10-16

T² / R3 est à peu près constant égal à : 3,15 10-16.

La 3ème loi de Kepler est bien vérifiée.

masse de Jupiter :

T² / R3 = 4p²/(GM) 3ème loi de Képler.

M = 4p² / ( 3,15 10-16 *6,67 10-11)=1,87 1027 kg.

à suivre ...
retour - menu
à bientôt ...