|
bac Amérique du Sud 12/00 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
||||||
|
|
Cet exercice étudie un modèle très simplifié du mouvement du centre d'inertie G d'un skieur dans différentes phases de son parcours. Masse du skieur m= 80 kg. Montée et plat: L'ensemble des forces de frottement est assimilé à une force unique, de sens opposé au vecteur vitesse, de norme constante F=50N. Le skieur reste constamment en contact avec le sol. 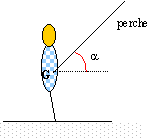
descente:
|
|||||
|
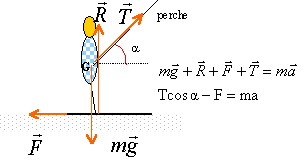
système : lskieur et équipement; référentiel terrestre galiléen. Ecrire la seconde loi de Newton, le skieur étant soumis à son poids, à l'action de la perche, à l'action du sol . projeter cette relation vectorielle sur un axe horizontal à droite.
T= (ma +F)/ cosa. calcul de l'accélération : v0² -v² init = 2a d avec v init = 0 a = v0² / (2d) = 2² / (2*8)= 0,25 m/s². T= (80*0,25+50) / cos45 = 99N.
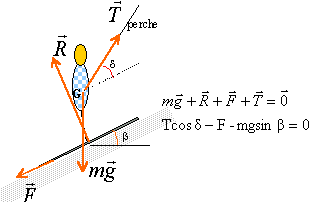
montée à vitesse constante : D'après le principe d'inertie la somme des forces est nulle. projection suivant un axe parallèle au plan vers le haut
T = (F+mgsinb) / cosd. T=(50+80*9,8*sin40) / cos30 = 639 N.
plate forme horizontale : théorème de l'énergie cinétique( seul fes frottements travaillent) ½ mv²fin- ½ mv²0 = -fd fd=½ mv²0 d'où d = 0,5*80 * 2² / 50 = 3,2 m. mouvement rectiligne uniformément freiné. v²fin- v²0 ==0- v²0 2ad d'où a = - v²0 / (2d) = -4 / 6,4 = -0,625 m/s². d = -½ at² + v0t ou mieux v = at + v0. t =(v-v0) / a = (0-2) / (-0,625) =3,2 s. plate forme horizontale :
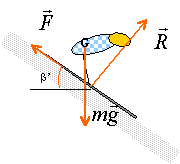
projection de la somme des forces sur un axe parallèle au plan dirigé vers le bas : mgsinb'-f = ma a = gsinb'-f /m = 9,8 * sin28 -50/80 = 4,6 - 0,625 = 3,975 m/s². v² -0 = 2ad v² =2*3,975 *300 = 2385 et v = 48,8 m/s =175,8 km/h. le poids et les forces de frottement travaillent (mgsinb' -f) AB variation d'énergie cinétique : ½mv² avec v = 107 /3,6 = 29,72 m/s théorème de l'énergie cinétique : ½mv² = (mgsinb' -f) AB mv² / (2AB) = mgsinb' -f f = mgsinb' -mv² / (2AB) f= 80[9,8*sin28 -29,72² / 600] = 250N.
lorsque la vitesse limite est atteinte la somme des forces appliquées au skieur est nulle. Projection de cette somme sur un axe parallèle au plan dirigé vers le bas : mgsinb'-f = 0 avec f = kv² v² = mgsinb' / k = 80*9,8 sin28 / 0,33 = 1115 vitesse limite = 33,4 m/s = 33,4*3,6 = 120,28 km/h.
|
||||||
|