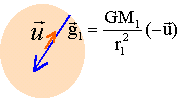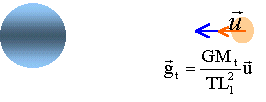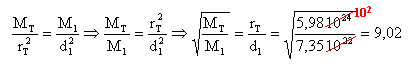|
Tintin entreprend un voyage de la terre à la lune . En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
||||||
|
|
Données : Masse de la Terre : Mt = 5,98.1024 kg Masse de la Lune : Ml = 7,35.1022 kg Rayon de la Terre : Rt = 6,38.103 km Rayon de la Lune : Rl = 1.74.103 km Constante de gravitation universelle : G = 6.67.10-11 S.I. On considère un satellite de la Terre ayant une orbite circulaire de rayon a et dont le centre est confondu avec le centre de la Terre. La période T du satellete est telle que : 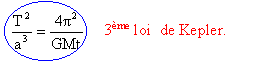
|
|||||
|
a3 = T² G Mt / (4p²) a3 = (2,36 106)²*6,67 10-11*5,98 1024/ (4*3,14²) =5,6 1025. a = 3,83
108 m.
champ à la surface de la lune : gl = 6,67 10-11* 7,35 1022 / (1,74 106 )² = 1,62 m/s². champ de gravitation crée par la terre à la surface de la lune :
gt = 6,67 10-11* 5,98 1024 / (3,83 108)² = 2,71 10-3 m/s². valeur négligeable devant le champ crée
par la lune à sa surface.
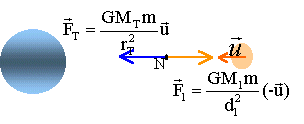
au point neutre N les forces attractives de gravitation se compensent ( sont opposées) : N est donc sur le segment de droite joignant les centres des deux planètes.
rT=9,02 dl. et rT+ dl =3,83 108 . rT+ rT /9,02 =3,83 108 . rT =3,83 108 *9,02 / 10,02 =3,44 108 m.
|
||||||
|