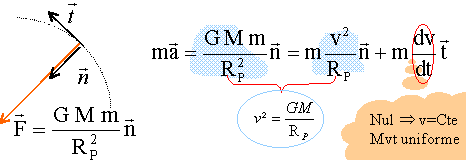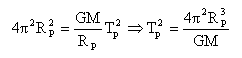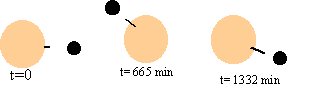|
la planète Mars et ses satellites naturels Antilles 06 / 01 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
||||||
|
|
document : Sur deux aspects au moins Mars est semblable à la terre. Tout d'abord elle tourne autour de son axe en 24h 37 min, ce qui fixe le jour martien à 41 minutes de plus que le jour terrien. Ensuite son axe est incliné de 25° sur le plan de son orbite ( 25 ° est l'angle entre l'axe de Mars et la normale au plan de son orbite), soit d'un degré et demi de plus que l'axe de la terre. Aussi, comme la terre, Mars est soumise à un cycle régulier de saisons. Les deux satellites de Mars - Phobos et Deimos- ont été découverts par Asaph Hall de l'observatoire de Washington. Phobos est un bloc de rocher allongé creusé de cratères. Son diamètre maximum ne dépasse pas 25 km. Il orbite si près de la planète (6000 km : altitude du centre de Phobos par rapport au sol martien) qu'il se lève et se couche deux fois par jour martien. (Phobos tourne sur son orbite dans le même sens que mars autour de son axe. Deimos est trois fois plus éloigné de Mars et encore plus petit que Phobos, son diamètre n'exède pas 6 km. données sur Mars : - période de rotation: T=24 h 37 min. - constante de gravitation universelle : G= 6,67 10-11 N m2 kg-2. - rayon martien Rm= 3400 km - masse de Mars: M - période de révolution de Phobos autour de Mars : Tp=7 h 39 min 14 s. - rayon de l'orbite autour du centre de Mars : Rp. questions : Détermination de l'ordre de grandeur de la masse de Mars gràce à l'étude du mouvement de Phobos :
L'ordre de grandeur d'une valeur est la puissance de 10 la plus proche. Un phénomène étonnant pour un terrien : Phobos orbite ci près de la planète qu'il se lève et se couche deux fois par jour martien .
|
|||||
|
dans un référentiel galiléen le principe d'inertie est vérifié.
Le satellite n'est soumis qu'à la force de gravitation centripète. Ecrire la seconde loi de Newton dans le repère de Frenet:
2pRP= v Tp. élever au carré : 4p² (RP)² = v² Tp ² remplacer v² par l'expression ci dessus:
masse de Mars :
application numérique : RP = 6000 + 3400 = 9400 km = 9,4 106 m TP= 7 *3600 + 39*60 + 14 = 27 554 s = 2,75 104 s. M = 4*3,14² *(9,4 106)3 / (6,67 10-11*(2,75 104)²) M = 4*3,14 ² * 9,43 1018 / (6,67*2,75² 10-3) M= 4*3,14 ² * 9,43 1021 / (6,67*2,75² ) M= 6,5 1023 kg.
la période de révolution de Phobos est de l'ordre de 7 h 39 min = 459 min la période de révolution de Mars est de l'ordre de 24 h 37 min = 1477 min A quelle date un observateur situé sur Mars voit il à nouveau Phobos passer pour la seconde fois au dessus de lui? L'origine des temps est prise au moment du premier passage de Phobos. angle balayé par Mars : qm= 2pt / Tm pendant le temps t angle balayé par Phobos :qP= 2pt / TP . au second passage , Phobos a fait un tour de plus que Mars. qP= qm+ 2p
t= 665 min
|
||||||
|