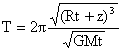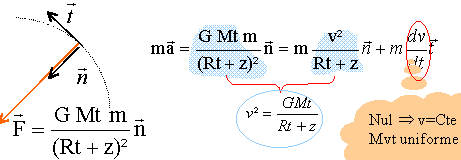Aurélie sept 2001

devoirs en terminale S

localisation d'un véhicule par GPS Asie 06 / 01


En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


document :

Le GPS permet de déterminer la position d'un mobile équipé d'un récepteur n'importe où sur le globe à l'aide de satellites. L'infrastructure utilisée est de 5 stations de contrôle au sol, de 24 satellites situés à 20 000 km d'altitude et répartis sur 6 orbites inclinées de 55° par rapport au plan de l'équateur. Chaque satellite heberge 4 horloges atomiques. Quatre satellites, au moins sur les 24, sont situés en permanence au dessus du récepteur.

Le principe de la localisation est simple : un signal radio contenant l'heure d'émission et la position exacte du satellite est émis simultanément sur deux fréquences : 1200 et 1500 MHz pour chaque satellite à intervalle de temps régulier. Le récepteur peut ainsi après réception, connaître le temps mis par l'information pour arriver jusqu'à lui. Connaissant la vitesse de propagation du signal, un simple calcul permet de déterminer la distance le séparant du satellite. En renouvellant l'opération avec au moins deux autres satellites, le récepteur, par triangulation, connaît sa position avec une précision approchant la dizaine de mètres.

Pour l'exercice, on utilisera deux hypothèses simplificatrices:

- l'ensemble du trajet des ondes se fait dans un milieu homogène isotrope d'indice de réfraction n=1.

- les satellites ont une orbite circulaire.

données :

- période de rotation ou jour sidéral : T=23 h 56 min 4s.

- constante de gravitation universelle : G= 6,67 10-11 N m2 kg-2.

- rayon terrestre Rt= 6378 km

- masse de la terre: Mt = 5,98 1024 kg.

- célérité de la lumière :c=2,998 108 m/s.

questions :

  1. Représenter le champ de gravitation en un point de l'orbite d'un des satellites et donner son expression vectorielle.
  2. Démontrer que le mouvement du satellite est uniforme.
  3. Montrer que la période de révolution est donnée par la relation suivante, où z représente l'altitude par rapport au niveau de la mer.
  4. Calculer la période T.
  5. Préciser ce qu'est un satellite géostationnaire.
  6. Indiquer si les satellites utilisés pour le GPS sont géostationnaires.
  7. Le texte parle d'un signal radio par les satellites: préciser de quel type d'ondes il s'agit.
  8. Indiquer la vitesse de propagation d'une telle onde dans le vide.
  9. Déterminer avec quelle précision la durée du trajet du signal doit être connue pour permettre la localisation du récepteur à 10 m près. On considère que la célérité de la lumière est parfaitement connue.
  10. Indiquer le type de dispositif embarqué dans les satellites permettant cette précision.

 

.
.

corrigé


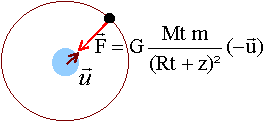
Le satellite n'est soumis qu'à la force de gravitation centripète.

Ecrire la seconde loi de Newton dans le repère de Frenet:

période T: durée necessaire pour parcourir la circonférence du cercle à la vitesse v.

2p(Rt+z)= v T

élever au carré : 4p² (Rt+z)² = v² T²

remplacer v² par l'expression ci dessus:

application numérique :

T² = 4*3,14² *(6,378 106 + 20,2 106)3 / (6,67 10-11*5,98 1024)= 1,85 109.

T= racine carrée (1,85 109) = 43085 s = 11 h 58 min.

géostationnaire :

le satellite tourne dans le même sens que la terre, à la même vitesse angulaire dans le plan de l'équateur. Il paraît fixe pour un observateur terrestre.

Les satellites utilisés pour le GPS ne sont pas géostationnaires.

1200 et 1500 MHz soit 1,5 109 Hz

ces ondes se propagent à la vitesse de la lumière soit 3 108 m/s

leur longueur d'onde est voisine de : 3 108 / 1,5 109 = 0,2 m

donc domaine des ondes radio de courte longueur d'onde.

Pour que le véhicule soit localisé dans un cercle de 10 m de diamètre, la précision sur le temps doit être de l'ordre de :

10 / 3 108 = 33 10-9 s = 33 ns

Une horloge atomique est capable d'avoir une telle précision.

à suivre ...
retour - menu
à bientôt ...