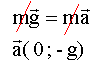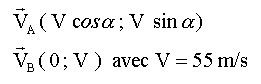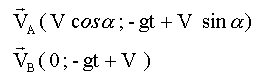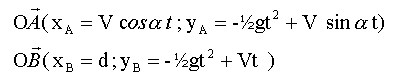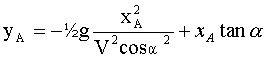|
feu d'artifice bac Amérique du nord 06 / 01 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
||||||
|
|
Pour un feu d'artifice deux fusées doivent être tirées simultanément à partir de deux points O et P situés au sol et séparés par une distance d=45 m. Ces fusées vont exploser à la date t=5s après leur lancement, l'une au dessus de l'autre et mélanger ainsi leur couleurs. La fusée B est tirée du point P avec une vitesse VB verticale. LafuséeA est tirée du point O avec une vitesse VA inclinée d'un angle a par rapport à l'horizontale. Les vecteurs vitesses précédents sont dans le même plan vertical. L'instant du lancement est choisi comme origine des temps. On négligera les frottements de l'air ainsi que la rotation des fusées sur elles mêmes. On suppose qu'il n'y a pas de vent. On prendra VA = VB = 55 m/s. 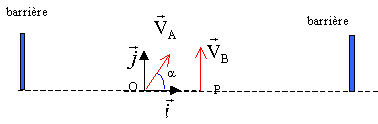
|
|||||
|
Les deux fusées sont soumises uniquement à leur poids, verticale vers le bas. La seconde loi de newton s'écrit :
le mouvment des fusées est uniformément
varié.
La fusée A est à l'origine du repère et la fusée B se trouve à l'abscisse xB=d=45; son ordonnée yB est nulle.
La fusée B a une trajectoire rectiligne verticale ( vecteur accélération et vecteur vitesse initiale colinéaires) La fusée A a une trajectoire parabolique
le vecteur vitesse est une primitive du vecteur accélération
le vecteur position est une primitive du vecteur vitesse :
les deux fusées se trouvent à l'abscisse xA= xB = 45 m et t=5s. 45 = 55 cos a *5 cos a = 0,163 et a = 80,6 °. à t=5 s , yB-yA = V t - V t sina = V t(1-sina) cette différence est positive : donc la fusée B explose 3,7 m au dessus de la fusée A
Quant à la fusée B, lancée verticalement, elle retombe en P en cas de non explosion. trajectoire de la fusée A: on élimine le temps t = xA / (V cos a) puis repport dans yA:
application numérique : yA = -0,061 xA² +6 xA. calcul de yA lorsque xA=155 m yA = -535 cette valeur étant inférieure à zéro, les spectateurs sont en sécurité. ou bien calculer l'abscisse de l'impact : 0 = -0,061 xA² + 6xA xA = 98,4 m valeur inférieure à 155 m
|
||||||
|