| |
lancer d'un ballon en gymnastique rythmique Pondichéry 05/01 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||
|
|||||||
|
|
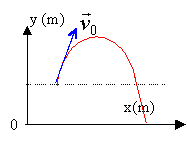
trajectoire |
Une gymnaste, tout en étant en mouvement, doit lancer en l'air un ballon et le rattraper. " On se propose de montrer dans cet exercice que pour être au bon moment et au bon endroit pour rattraper un ballon préalablement lancé en l'air, une solution simple pour la gymnaste consiste à lancer le ballon avec une vitesse verticale et à continuer son déplacement horizontal en gardant une vitesse constante. La coïncidence en temps et en lieu sera ainsi assurée et, cela, quelle que soit la grandeur de la vitesse verticale donnée au ballon. "D'après un extrait de l'ouvrage : Physique pour les sciences du sport (Alain Durey) Dans un référentiel lié à la salle de gymnastique, la gymnaste est en mouvement rectiligne uniforme à la vitesse V1. Dans ce même référentiel à l'instant du lancer la vitesse du ballon est V0 dont la composante horizontale V0x est égale à V1. Sa composante verticale V0z sera notée V2. L'instant du lancer est choisi comme origine des dates t = 0. Dans le référentiel de la salle ; on considère le repére (O, i, k) défini de la manière suivante : l'origine O correspond à la projection du centre d'inertie G0 de la gymnaste sur le sol horizontal à l'instant du lancer ; l'axe Ox est horizontal et l'axe Oz vertical ascendant. Le centre B du ballon se trouve au point B0 de coordonnées ( x0 ; z0 ) à l'instant du lancer. 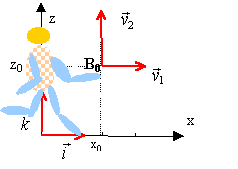 1 - Mouvement de la gymnaste Déterminer l'équation horaire xG(t) du mouvement du centre d'inertie G de la gymnaste sur l'axe Ox. 2 - Mouvement du ballon a) De l'étude dynamique du mouvement du centre d'inertie B du ballon déduire les équations horaires xB(t) et zB(t) du point B. b) En déduire l'équation de la la trajectoire du point B et tracer l'allure de la courbe correspondante en y faisant apparaître le vecteur V0 c) Quelles sont les caractéristiques du vecteur vitesse du point B au sommet de sa trajectoire ? Quelle est la hauteur maximale atteinte par le point B ? 3 - Rattraper le ballon par la gymnaste a) La gymnaste récupère le ballon lorsque son centre B repasse à l'altitude z0. Déterminer le "temps de vol" tV du ballon (durée séparant les instants du lancer et du rattraper).Comment la gymnaste peut-elle augmenter ce "temps de vol" ? Dans la salle le champ de pesanteur uniforme est noté g. Dans tout le problème on négligera l'action de l'air. Aucun calcul numérique n'est demandé. Toutes les réponses seront exprimées en fonction des données : g, V1, V2, x0 et z0. b) Déterminer la distance parcourue par le centre d'inertie B du ballon suivant l'axe horizontal Ox pendant le "temps de vol'' .De quel(s) paramètre(s) dépend cette distance. c) Montrer que la distance parcourue par le centre d'inertie G de la gymnaste pendant ce "temps de vol" est la même. 4 - Critique du texte introductif a) Dans l'extrait de l'ouvrage cité en début d'exercice deux vitesses sont mentionnées. Dans quel référentiel chacune est-elle définie ?
|
|||||
| |
x(t) = V1 t Le ballon une fois lancé est en mouvement de chute libre : il n'est soumis qu'à son poids. Son accélération est l'accélération de la pesanteur . vecteur accélération (0; -g) vecteur vitesse initiale ( V1 ; V2) vecteur position initiale ( x0 ; z0) vecteur vitesse à la date t (V1 ; -g t +V2) vecteur position à la date t ( x=V1t + x0 ; y = -½ gt²+V2 t + z0) trajectoire : t = (x-x0) /V1. y = -½g (x-x0)² /V²1+V2/V1(x-x0)+ z0
au sommet de la parabole, la composante horizontale de la vitesse est V1 alors que la composante verticale de la vitesse est nulle. -gt + V2=0 où t = V2 / g. repport dans y : y = -½ gt²+V2 t + z0 y= - ½ gV²2 / g² +V2 *V2 / g + z0 = ½ V²2 / g + z0. la gymnaste rattrappe le ballon : y = z0 . z0 = -½ gtv²+V2 tv + z0 0 = -½ gtv²+V2 tv soit 0 = -½ gtv+V2 ou tv = 2 V2/g. en augmentant la composante verticale de la vitesse elle augmente le temps de vol distance parcourue par le ballon sur l'horizontale pendant le temps de vol: abscisse de B : x =V1tv + x0 = 2V1* V2/g + x0. distance : x-x0 = 2V1* V2/g distance parcourue par le centre d'inertie de la gymnaste durant ce temps de vol : x= V1 tv = 2V1* V2/g. La coïncidence en temps et en lieu sera ainsi assurée et, cela, quelle que soit la grandeur de la vitesse verticale donnée au ballon.
|
||||||
| |
|
||||||