Les constructions géométriques sont à faire sur la feuille en annexe 2 (à rendre avec la copie).

1. Images d'un objet réel AB dans un miroir plan et un miroir sphérique :
   a) Construire géométriquement l'image A'B' de la flèche AB dans le miroir plan de la figure l. Que vaut le grandissement g ?

   b) On considère le miroir sphérique de foyer F (figure 2).
   - Où se trouve l'image de l'objet AB si ce dernier est placé à une très grande distance (éloigné à l'infini) sur l'axe optique, à gauche du miroir sphérique ?
   - Construire géométriquement l'image de la flèche AB telle qu'elle est placée sur la figure pour le miroir sphérique.

2. Etude du télescope :
   Un télescope de NEWTON est essentiellement constitué d'un miroir sphérique concave, optique D de sommet S, de foyer F, et de distance focale f = SF₁. On souhaite observer un objet éloigné à l'infini (étoile, planète, Lune, ...) dans la direction de l'axe optique D du miroir. Le télescope est équipé d'un oculaire assimilable à une lentille mince convergente de distance focale f'₂ (f ₂ > 0) et de foyers F₂ et F'₂. 
   On souhaite que l'observation se fasse selon un axe D' perpendiculaire à l'axe D. C'est pourquoi on place un miroir plan incliné à 45° par rapport à D, de centre I situé sur cet axe entre le foyer F, et le sommet S du miroir sphérique.
   a) - Sur la figure 3, indiquer la position de l'image F', de F, dans le miroir plan. - L'axe D ' de l'oculaire est perpendiculaire en I à D. Le réglage du télescope est afocal : dans ces conditions, F', et F₂ sont confondus.
   - Placer l'oculaire sur la figure 3. On ne tiendra pas compte sur le dessin des valeurs relatives de f, et f'₂ données ultérieurement.
   - Si l'objet observé est à l'infini sur D où se trouve son image finale ?
   b) L'astronome désire observer la Lune (considérée comme infiniment éloignée et de centre situé sur D ). Le rayon lumineux issu du bord supérieur de la Lune A_oo, arrive en S en faisant l'angle a supposé faible avec D (voir figure ci-dessous)

   - Justifier que q= 2a est le diamètre apparent de la Lune observée à l'œil nu. Où se trouve l'image A₁ de A_oo pour le miroir sphérique ?
   - Soit B₁ l'image de B_oo bord inférieur de la Lune. Quelle relation existe-t-il entre A₁B₁ f, et q ? On suppose q petit : tan q = q . Que vaut A₂B₂, image de la Lune dans le miroir plan ?
   - Calculer numériquement A₂B₂ si f, = SF, = 1,20 m ; q= 2a = 30' d'arc = 0,00872 rad.
   c) Le télescope étant afocal, l'astronome observe la Lune dans l'oculaire.
   - Sur la feuille annexe 2 (à rendre avec la copie), faire un schéma de l'oculaire (axe optique D ' foyers F₂ et F'₂) sur lequel on placera A₂B₂.

   

   - Où se trouve l'image de la Lune dans l'oculaire (image finale) ?
   - Soit a ' l'angle d'inclinaison sur D ' du rayon passant par A₂ et le centre de l'oculaire. Exprimer a ' (supposé petit) en fonction de a, f₁ et f ’₂.
   - Justifier que q'= 2a' est le diamètre apparent de la Lune vue dans le télescope.
   d) On donne : f '₂ = 2,00 cm.
   - Comment appelle-t-on le quotient q'/ q = a'/ a ? Justifiez ce nom !
   - Calculer la valeur numérique de ce rapport. 

---

. .

---

corrigé

---

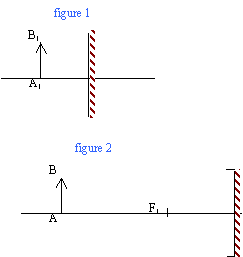
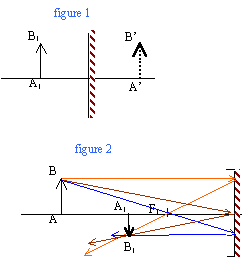
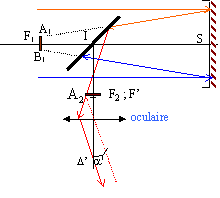
l'image A'B' de AB donnée par le miroir plan, est symétrique de AB par rapport au plan du miroir. Cette image est virtuelle.

le grandissement est égal à 1.

---

l'image F' de F donnée par le miroir plan est symétrique de F par rapport au plan du miroir plan.

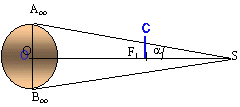
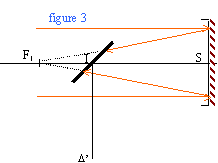
Si l'objet est à l'infini sur D :

l'image A₁B₁ donnée par le miroir sphérique est en F₁.

l'image A₂B₂ donnée par le miroir plan de l'objet A₁B₁ est en F' ou F₂.

l'image A'B' donnée par l'oculaire de l'objet A₂B₂ est à l'infini.

---

diamètre apparent q voisin de A_ooB_oo / OS, avec O centre de la lune

par raison de symétrie q = 2a

Si l'objet est à l'infini sur D, l'image A₁B₁ donnée par le miroir sphérique est en F₁.

A₁B₁ = q f= 0,00872*1,2 = 1,046 10^-2 m = 1,046 cm.

l'image A₂B₂ donnée par le miroir plan de l'objet A₁B₁ est en F' ou F₂. Cette image est symétrique de A₁B₁ par rapport au miroir plan ; sa grandeur est identique à celle de A₁B₁.

---

l'image de la Lune donnée par l'oculaire est à l'infini.

a' = ½ A₂B₂ / f₂ avec A₂B₂ = q ' f d'où a' = ½ q' f / f₂

par raison de symétrie q' = 2a'.

le grossissement est égal à q' / q.

rapport entre l'angle sous lequel est vue l'image définitive ( donnée par le télescope) et l'angle sous lequel la lune est vue à l'oeil nu.

q' / q = f / f₂ = 1,2 / 0,02 = 60.

---