|
Notice d'une lunette astronomique sept 01 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
||||||||||||||||
|
||||||||||||||||
|
|
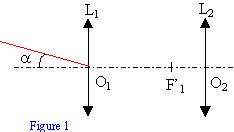
Le but de cet exercice est d'étudier le fonctionnement d'une lunette astronomique et de vérifier certaines indications portées sur la notice descriptive. Lunette astronomique : - Grossissements: 32 ; 51 ; 107 ; 64 ; 102 ; 214. - Objectif: achromatique, de diamètre 80 mm, de focale 640 mm. - Oculaires : trois oculaires interchangeables de focale 20 mm ; 12,5 mm ; 6 mm. - Lentille de Barlow (elle double le grossissement de la lunette pour chaque oculaire). Une lunette astronomique est constituée de deux systèmes optiques convergents assimilés à deux lentilles minces. L 'objectif (lentille L1 de centre optique O1) pointe dans la direction de l'astre, objet de 1 'observation. L'oculaire (lentille L2 de centre optique 02) est situé devant l'œil de l'observateur. Le foyer principal image F'1 de 1'objectif est confondu avec le foyer principal objet F2 de 1 'oculaire. Modèle réduit de la lunette :
Grossissement du modèle : On appelle a l'angle entre l'axe optique et un rayon issu de B (B situé à l'infini) comme indiqué sur la figure 1 ci dessus. On appelle a' l'angle entre l'axe optique et le faisceau lumineux sortant de L2 venant de B1. Le grossissement d'une lunette est défini par G = a'/a. On considère que a et a' sont petits.
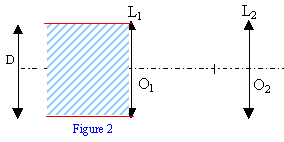
Gain en luminosité : On envisage maintenant un faisceau incident de rayons lumineux parallèles entre eux et parallèles à 1'axe optique de la lunette. Ce faisceau, centré sur 1'axe optique, a même diamètre D que 1'objectif L1. On note d le diamètre du faisceau qui émerge de l'oculaire L2
Un des principaux rôles d'une lunette astronomique est de collecter le maximum de lumière provenant d'un objet ponctuel très éloigné. Sachant que le diamètre d'une pupille dilatée est de l'ordre de 8 mm, la lunette est un bon collecteur de lumière car dmax est inférieur à 8 mm.
|
|||||||||||||||
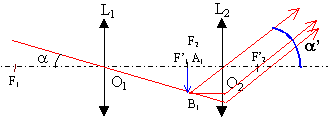
L'objet étant situé à l'infini, l'image A1B1 se trouve dans le plan focal image de L1. Cette image est réelle et a le sens contraire de l'objet. A1 se trouve au foyer principal objet de L2. En conséquence l'image définitive A'B' est à l'infini.
conditions de Gauss: - objet de petites dimensions placé au voisinage de l'axe optique principal - éliminer en diaphragmant les rayons trop inclinés sur l'axe optique principal. tan a = A1B1 / O1F'1 voisin de a en radian si a petit . tan a' = A1B1 / O2F'2 voisin de a' en radian si a' petit . a O1F'1 =a' O2F'2 grossissement = a' /a =O1F'1 / O2F'2 .
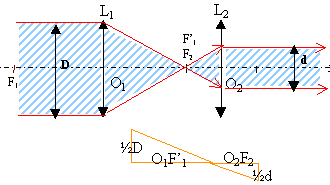
les deux triangles ci dessus sont semblables: ½D / (½d )= O1F'1 / O2F2. d = D O2F2 / O1F'1= D / grossissement
|
||||||||||||||||
|