Aurélie juin 2001

devoirs en terminale S

image du soleil donnée par 2 lentilles .

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.




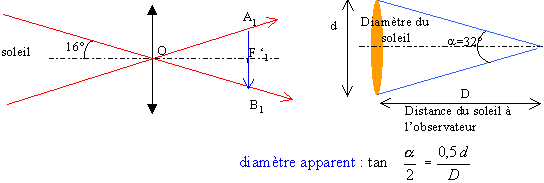
Une lentille mince convergente de distance focale f ' 1 =1 m , a son axe principal dirigé vers le centre du soleil dont la distance à la lentille est considérée comme infinie. Le diamètre apparent du soleil est de 32 '.

  1. Déterminer la grandeur et la position de l'image du soleil donnée par cette lentille. Faire également la construction de cette image.
  2. A 50 cm derière cette image on désire obtenir une image réelle et agrandie de cette première image. Pour cela on dispose d'une lentille convergente de distance focale f '2= 5 cm.
    - Déterminer la position de cette lentille.
    - Quelle est alors la grandeur de l'image définitive?

corrigé

L'image du soleil (objet à l'infini ) se trouve dans le plan focal image de la première lentille.

32 minutes d'angle à exprimer en radian : 32/60 = 0,5333 °

puis 0,5333 *3,14 /180 = 9,3 10-3 rad.

donc tan 16 ' voisin de 4,65 10-3 .

Dans le triangle OF'1B1 : tan 16 ' = F'1B1 / f ' 1 = 4,65 10-3 .

A1B1 = 4,65 10-3 *2 = 9,3 10-3 m.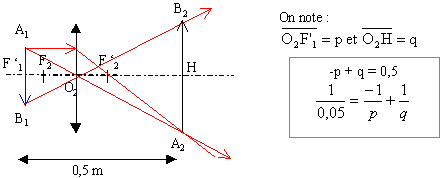

résoudre le système de 2 équations à 2 inconnues p et q

20 pq = p-q (réduction au même dénominateur)

pq = -0,5 /20 = -0,025

p(0,5+p) + 0,025 = 0

p² +0,5 p + 0,025 =0

d'où p = - 0,056 m et q = 0,443 m

la deuxième lentille est donc située 55,6 cm derrière la première lentille.

grandissement de la seconde lentille : q / p = 0,443 / (-0,056)= - 7,9

l'image est en sens inverse de la première image ( grandissement négative)

dimension de l'image définitive : 7,9 *9,3 10-3 = 7,35 10-2 m.

 


à suivre ...
retour - menu
à bientôt ...