| |
le champ magnétique bac 06/00
|
||||||
| |
|
||||||
|
|
champ uniforme |
On désire étudier le champ magnétique à l'intérieur d'un solénoïde. Cette étude comporte différentes parties. I - étude qualitative : 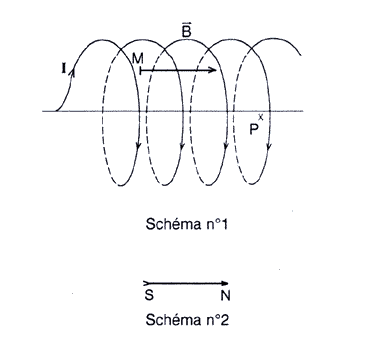
Le champ magnétique est représenté en un point M situé à l'intérieur du solénoïde (voir schéma n°1). On place au point M la petite aiguille aimantée dessinée ci-dessous (schéma n°2). Reproduire rapidement le schéma du solénoïde sur la copie et dessiner l'aiguille aimantée au point M en précisant clairement son orientation et ses pôles Nord et Sud. On place ensuite cette aiguille aimantée au point P. Son orientation va-t-elle changer ? Justifier. II - étude quantitative : On place maintenant en un point intérieur au solénoïde une sonde permettant de mesurer l'intensité notée B du champ magnétique créé par un courant électrique continu d'intensité I qui parcourt le solénoïde. On fait varier I et on mesure B pour diverses valeurs de I. On trace ensuite le graphe représentant les variations de B en fonction de I (voir schéma n°3).
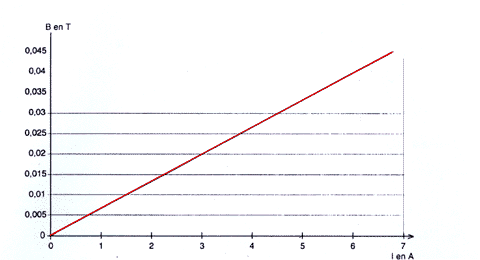
- Quelle est la nature du graphe ? - En déduire le type de relation mathématique simple existant entre B et I. - Quel est le nom de l'unité correspondant à la lettre T ? - On montre que la relation exprimant B en fonction de I est la suivante : B = m0 n I. = 4 p 10-7 n I avec n = N / L Dans cette expression, N est le nombre de spires du solénoïde et L sa longueur exprimée en mètres. Le nombre de spires N du solénoïde étant inconnu, on essaie de le déterminer. Pour cela on fixe la valeur de l'intensité à I = 6 A et on pratique comme suit : A partir du graphique, préciser la valeur de B correspondant à cette valeur d'intensité I = 6 A (la méthode employée n'est pas à expliquer). En vous servant de la relation reliant B et I, déduire le nombre N de spires du solénoïde sachant que la longueur du solénoïde a pour valeur L = 0,3 m. III champ crée et champ magnétique terrestre : - Donner l'ordre de grandeur de la valeur BT du champ magnétique terrestre. - Le graphe précédent montre que pour une intensité I=3 A, la valeur B du champ magnétique crée est de l'ordre de 2.10-2 T. Ce champ magnétique est-il : a) environ 10 fois plus intense que le champ magnétique terrestre ? b) environ 1000 fois plus intense que le champ magnétique terrestre ? c) environ 10 fois moins intense que le champ magnétique terrestre ? d) environ 1000 fois moins intense que le champ magnétique terrestre ? IV - la résonance magnétique nucléaire : La résonance magnétique nucléaire nécessite des champs très intenses, supérieurs à 1 T. Citer un moyen de produire un tel champ.
|
|||||
| |
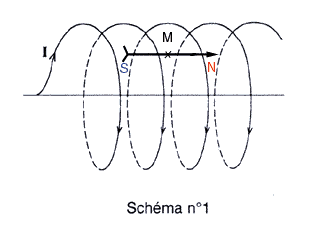
En M, l'aiguille aimantée s'oriente selon , le vecteur champ "sortant" par son pôle Nord. En P, si le solénoïde est "long" (l > 5 x diamètre), le champ magnétique est uniforme à l'intérieur. donc l'orientation de l'aiguille est identique. Etude quantitative Le graphe de B = f(I) est une droite passant par l'origine du repère ; B est donc proportionnel à l'intensité I : B = k . I avec k = constante Le tesla , notée T est l'unité de champ magnétique. Sur le graphique, l'ordonnée du point d'abscisse I = 6 A est : B = 0,04 T N = B L / (4p10-7 I) N= 0,04 *0,3 / (4*3,14 10-7 *6) = 1592 spires.
Champ créé et champ magnétique terrestre Valeur approximative de la composante horizontale du champ magnétique terrestre : BT= 2 10-5 T Pour I = 3A, B = 2.10-2T : ce champ magnétique est donc 1 000 fois plus intense que l'ordre de grandeur du champ magnétique terrestre.
La résonance magnétique nucléaire pour produire des champs magnétiques très intenses, il faut un solénoïde : - comportant un grand nombre de spires par unité de longueur : N/L - et parcouru par un courant de forte intensité : I - la présence d'un noyau de fer doux dans le solénoïde permet d'augmenter encore la valeur du champ magnétique.
|
||||||
|
|
|