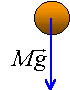|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||
|
||||||
|
|
Une bille est en chute libre sans vitesse initiale.
corrigé |
|||||
|
l'origine des altitudes est prise au sol noté S état initial en A : vitesse nulle (donc pas d'énergie cinétique) ; altitude h état final juste avant d'arriver au sol S : vitesse v (énergie cinétique ½mv² ) ; altitude nulle travail du poids moteur ( quand ça descent ): WA-->S = mgh variation énergie cinétique ½mv²-0 la variation d'énergie cinétique est égale au travail du poids : ½mv²-0 = mgh d'où : v² = 2gh. la vitesse est indépendante de la masse : v² = 2*9,8 *14 = 274,4 prendre la racine carrée : v = 16,56 m/s.
état final B: vitesse v (énergie cinétique ½mv² ) ; altitude z variation d'énergie cinétique : ½m(v² -vo²) travail du poids résistant (ça monte) : WA-->B = mg(zo-z) la variation d'énergie cinétique est égale au travail du poids : ½m(v² -vo²) = mg(zo-z) v² = vo²+2g(zo-z). à l'altitude maximale atteinte , la vitesse est nulle ; de plus zo =0 d'après le texte. vo² = v² +2gz vo² = 2*9,8*10 = 196 et vo =14 m/s. vo² = 2*9,8*100 = 1960 et vo = 44,27 m/s.
|
||||||
|
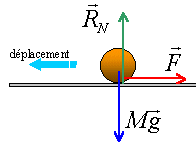
Une automobile de masse m= 900 kg lancée à 100 km/h freine brutalement en bloquant ses 4 roues. On suppose qu'elle poursuit son mouvement dans l'axe de la route horizontale. Elle s'arrête au bout de 97,0 m, ce qui représente une durée de 6,54 s.
corrigé référentiel terrestre galiléen exprimer la vitesse en m/s : 100 / 3,6 = 27,77 m/s.
énergie cinétique juste avant le freinage : 0,5* 900*27,77² = 347 000 J = 347 kJ énergie cinétique finale nulle à l'arrêt de la voiture variation énergie cinétique : 0 -347 000 = -347 000 J. la voiture est soumise à :
poids vertical vers le bas 900*9,8 N, perpendiculaire à la vitesse donc le poids ne travaille pas. action du sol perpendicualre au sol vers le haut ; cette action perpendiculaire à la vitesse ne travaille pas. la force de freinage parallèle à la route de sens opposé à la vitesse. travail résistant des frottement = - 97 F le travail des frottements est égal à la variation de l'énergie cinétique : - 347 000 = -97 F F = 3580N. puissance moyenne des frottements =travail des frottements / durée du freinage -347 000 / 6,54 = -53 000 watts.
|
||||||
|
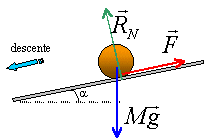
Une voiture de masse m= 800 Kg roule à une vitesse V=72 km/h sur une route rectiligne en pente descendante, faisant un angle de 4° avec l'horizontale. A partir d'une position A de la voiture, le conducteur freine en catastrophe et bloque ses 4 roues non équipé de l'ABS. Il s'arrête à la position B au bout de 92,0 m.
corrigé exprimer la vitesse en m/s : 72 / 3,6 = 20 m/s
le véhicule est soumis à : son poids vertical vers le bas l'action du plan perpendiculaire au plan : une force perpendiculaire à la vitesse ne travaille pas. la force de freinage F parallèle au plan vers le haut du plan. son travail est : WA-->B(F) = -92 F on descend le travail du poids est moteur : WA-->B(P) = mg (hA - hB) avec hA - hB = AB sin 4 = 92 * 0,0697 = 6,41 m WA-->B(P) = 800*9,8*6,41 = 50314 J. énergie cinétique initiale : 0,5 *800 *20² = 160 000 J énergie cinétique finale nulle : variation énergie cinétique :-160 000 J cette variation est égale à la somme des travaux des forces : -160 000 = 50 314 - 92 F F = 2286 N environ 4 fois plus faible que le poids. poids =9,8 *800 = 7840 N |
||||||
|
Un skieur à l'épreuve du kilomètre lancé (KL), en recherche de vitesse sur une piste plane, bien damée et inclinée d'un angle a = 26,0° par rapport à l'horizontale, atteint une vitesse de 182 Km/h au bout d'un km de piste. La masse du skieur et de son équipement est de 115 Kg.
corrigé sans frottement seul le poids travaille, l'action du sol est perpendiculaire au sol : départ A; arrivée B mg(hA - hB) = avec hA - hB = 1000 *sin 26 = 438,4 m 115*9,8 *438,4 = 494 000 J. énergie cinétique initiale nulle énergie cinétique finale : 0,5 mv² variation énergie cinétique : 0,5 *115 v² = 62,5 v² la variation d'énergie cinétique est égale au travail du poids : 57,5 v² = 494 000 v² =8590 et v =92,7 m/s. 92,7 *3,6 = 334 km/h. en tenant compte des frottements supposés constants : 182 /3,6 = 50,55 m/s variation énergie cinétique : 0,5*115*50,55² = 146 962 J 146 962 = travail du poids + travail des frottement W frottement = 146 692 - 494 000 = -347 000 J.
|
||||||
|