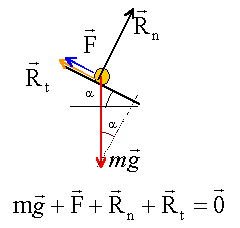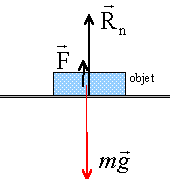
La poussée d'Archimède :

Un objet ancien homogène en étain de volume V=1L repose au fond d'une épave.

Masse volumique eau = 10³ kg . m^-3 ; masse volumique étain = 5,75 * 10³ kg . m ^-3 .

1. Faire l'inventaire des forces qui s'appliquent sur l'objet.
2. Calculer le poids de l'objet et la poussée d'Archimède qui s'appliquent sur l'objet.
3. En déduire la réaction que l'épave exerce sur l'objet.
4. Pour faire remonter l'objet on accroche à l'objet un ballon gonflé d'air. A la profondeur où se situe l' épave on peut considérer que la masse volumique de l'air emprisonné vaut 12 kg m ^-3 . Quel doit être le volume du ballon pour que la remontée de l'objet soit possible.

A bicyclette :

1. Sans pédaler, 1 cycliste descend 1 côte rectiligne de pente p = 6 % à la vitesse constante V = 25 km /h. La masse du système { cycliste +bicyclette } est M = 80 kg . On décompose la réaction de la route sur chaque roue en une composante normale R_n et une composante parallèle à la routr R_t ; R_t = 5,0 N sur chaque roue. Calculer la valeur F de la force de frottement de l'air sur le système {cycliste + bicyclette }.
2. Le cycliste roule sur une route horizontale à la même vitesse. La force de frottement exercée par la route sur la roue avant à la même valeur qu'à la 1^ère question . Il en est de même pour la force de frottement de l'air.
   - représenter la composante Rt' de la force de frottement sur la roue arrière. Dans ce cas la roue arrière est motrice.
   - calculer la valeur Rt' de cette force de frottement.
3. Même question si le cycliste monte maintenant une côte de pente 6 % .

    

---

corrigé :

sin a = 0,06 ; vitesse constante donc la somme vectorielle des forces est nulle.

projection de cette relation sur un axe parallèle au plan, orienté vers le bas :

mg sin a -F-Rt = 0 donne F = mg sin a -Rt

avec mg sin a = 80*9,8*0,06 = 47,04 N et Rt = 2*5 = 10 N

donc F = 47,04-10 = 37,04 N.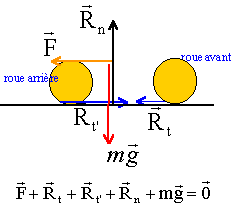

---

le poids et l'action du sol Rn sont opposées.

projection de cette relation sur un axe parallèle au plan, orienté à droite :

-R_t -F + R_t' =0 donc R_t' = R_t + F

attention ici R_t = 5 N (frottement résistant sur la roue avant)

R_t' = 5 + 37,04 = 42,04 N.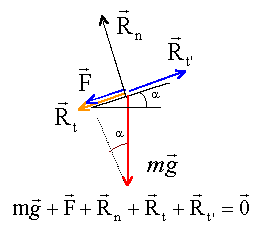

---

projection de cette relation sur un axe parallèle au plan, orienté vers le haut :

-mg sin a -F-R_t +R_t' = 0 donne R_t' = mg sin a + R_t + F

avec mg sin a = 80*9,8*0,06 = 47,04 N ; R_t = 5 N ; F = 37,04 N

donc R_t' = 47,04 + 5 + 37,04 = 89,08 N.

---