|
rotation et translation d'un cube En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||
|
||||||
|
|
Deux jumeaux de même masse m=75,0 kg montent au 5 ème étage d'un immeuble en partant du rez-de-chaussée. Le jumeau A emprunte l'ascenseur et le jumeau B l'escalier. La distance entre le plancher du RDC et lentre le plancher du 5 ème est de 16,5 m.
corrigé |
|||||
|
Le référentiel est la surface de la terre. travail du poids = mg( h départ - h fin) l'origine des altitudes est prise à la surface du sol. W = 75*9,8 *(0-16,5) = - 12127 J. Dans le référentiel de l'ascenseur, A est immobile : il n'y a pas de travail lorsqu'il n'y a pas de déplacement. |
||||||
|
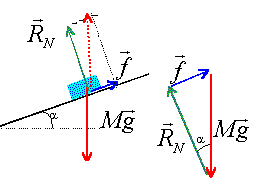
Un skieur de masse m=90,0 kg descend une piste inclinée d'un angle de 14° sur l'horizontale à une vitesse constante de 70,0 km/h. Les forces de frottement de la piste sur les skis ainsi que celles de l'air ont une résultante F parallèle à la pente.
d'après le principe d'inertie, le mouvement du skieur étant rectiligne uniforme, ce dernier est pseudo-isolé ( somme des vecteurs forces égale zéro).
dans le triangle des forces : F= Mg sin a = 90*9,8*sin14 = 213,3 N. travail de cette force : vecteur force et vecteur déplacement colinéaires et de sens contraire W = F * déplacement * cos 180 = - 213,3* 100 = - 21 330 J . Puissance de cette force : force de frottement et vitesse, vecteur colinéaires et de sens contraire Puissance = F v cos 180 exprimer la vitesse en m/s : 70 /3,6 = 19,44 m/s. puissance = -213,3*19,44 = -4146 W. travail du poids : La somme des forces est nulle, en conséquence la somme des travaux des forces est nulle. Rn, perpendiculaire au sol ne travaille pas le travail du poids est donc opposé au travail de la force F .
|
||||||
|
Pour préparer un sportif à une compétition de lancer de poids, (m=7,30 kg), on simule son geste ; voici les résultats obtenus en notant G le centre d'inertie de la boule. Hauteur du point O où le poids quitte la main du lanceur : 1,90m. Hauteur maximale atteinte par le poids : 4,50m à une distance de O égale à 6,72 m (point S). Distance horizontale du lancer : 16,20m (point D). Durée du lancer : 1,64 s. 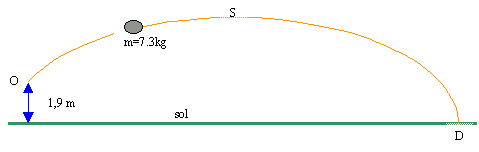
corrigé Le travail d'une force constante ne dépend pas du chemin suivi, mais uniquement des positions initiale et finale : Le référentiel est la surface de la terre. travail du poids = mg( h départ - h fin) l'origine des altitudes est prise à la surface du sol. W = 7,3*9,8*(1,9-0) = 136 J. entre les points O et S, le travail du poids est résistant (négatif) : l'altitude finale étant supérieure à l'altitude de départ. la vitesse du poids est inférieure à la vitesse initiale en O. entre les points S et D, le travail du poids est moteur (positif) : l'altitude finale étant inférieure à l'altitude de S. la vitesse du poids est supérieure à la vitesse initiale en S, mais reste inférieure à la vitesse initiale tant que l'altitude dépasse 1,9 m. la vitesse du poids est supérieure à la vitesse initiale en O ( entre S et D) lorsque l'altitude du poids est inférieure à 1,9 m. |
||||||
|
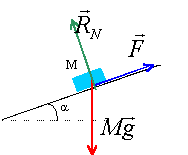
un tapis roulant est utilisé pour charger du minerai dans un wagon. La longueur du tapis est L = 22,5 m et son inclinaison avec l'horizontale est a = 35°
corrigé Le bloc de pierre est soumis à son poids et à l'action du tapis: celle ci peut être représentée par deux forces l'une f parrallèle au tapis et l'autre perpendiculaire au tapis La vitesse est constante et le mouvement rectiligne alors la somme vectorielle des forces est nulle.
f = Mg sin 35 = 2*9,8 sin 35 = 11,2 N. travail de cette force : force et déplacement sont colinéaires et de même sens donc le travail est égal à : f L = 11,2*22,5 = 253 J. vitesse de chargement : 1550 kg en 60 s soit 1550/60 = 25,8 kg / s La puissance (watt) mise en jeu est le travail (J) effectué à chaque seconde. 253 J pour déplacer 2 kg. on peut déplacer 25,8 kg / s donc : P = 253*25,8 / 2 = 3264 watts. |
||||||
|
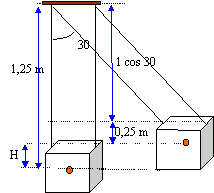
Rotation et translation d'un cube homogène : Un cube homogène, de masse m = 100 kg et d'arête a = 50 cm, peut être suspendu de deux facons. Dans le schéma 1, il est suspendu à une tige rigide de longueur L = 1 m. Cette tige pivote autour d'un point O, mais est fixée rigidement au centre C de la surface supérieur du cube. Dans le schéma 2, il est suspendu à deux cordes parallèles de même longueur L = 1 m. Ces cordes sont fixées en O1 et O2 sur la même horizontale et attachées au cube par les centres A1 et A2 des deux arêtes parallèles de sa face supérieure. Au départ, la tige et les deux cordes sont verticales. On déplace le tout jusqu'à ce que la tige ou les cordes fassent un angle de 30° avec la verticale. Déterminer le travail du poids du cube dans les deux cas. corrigé 
travail du poids lors du déplacement de la position verticale à la position oblique. l'altitude du centre d'inertie du cube (position verticale) est prise comme origine des altitudes W = mg (0- h) avec h = 1,25 -1,25 cos 30 = 0,167 m m =100 kg ; g = 9,8 N / kg W = - 100*9,8*0,167 = -163,6 J.
travail du poids lors du déplacement de la position verticale à la position oblique. l'altitude du centre d'inertie du cube (position verticale) est prise comme origine des altitudes W = mg (0- H) avec H = 1,25 -(0,25 +1 cos 30) = 0,134 m m =100 kg ; g = 9,8 N / kg W = - 100*9,8*0,134 = -131,3 J.
|
||||||
|