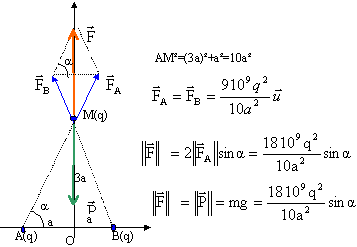|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||
|
||||||
|
|
Un solide subit 3 actions représentées par 3 vecteurs forces: F1 ; F2 ; F3 coplanaires. Elles s'appliquent en son centre d'inertie C, confondu avec le centre O d'un repère orthonormé du plan (O, i, j). On donne F1= -6 i et F2=3N. L'angle entre i et F2 vaut (i,F2)=45°. 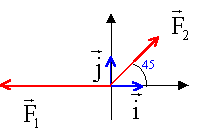 Déterminer graphiquement et par le calcul le vecteur force F3 pour que le solide soit en équilibre. corrigé |
|||||
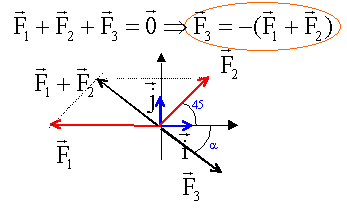
par le calcul : La relation vectorielle ci-dessus conduit à deux relations, projections sur chaque axe -6 + F2 cos45 + x3=0 -6 +3 *0,707 + x3= 0 x3= 6- 2,12 = 3,88 N 0 + F2 sin 45 + y3=0 3 *0,707 + y3=0 y3= -2,12 N angle a entre i et F3 : tan a = y3 / x3 = -2,12 / 3,88 = 0,546 a = 28,6°. norme de F3 : racine carrée ( (-2,12)² + 3,88 ² )= 4,42 N. |
||||||
|
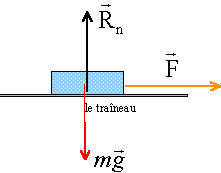
Un traineau de masse m = 150 kg est tiré par des chiens sur un plan horizontal. Les frottements agissant sur le traineau sont opposés au déplacement et assimilables à une force f horizontale de valeur considérée comme constante f = 400 N. L'attelage des chiens exerce sur le traineau une force F horizontale.
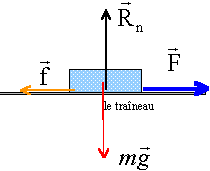
poids et action normale du support Rn sont opposées: ces vecteurs ont même norme mg =Rn = 150*9,8 = 1470 N. translation rectiligne uniforme: le vecteur vitesse est constant la somme vectorielle des forces est nulle. f (frottement) et F (motrice) sont opposées et ont même norme . f = F = 400 N. translation rectiligne accélérée: la vitesse augmente la force motrice a une norme supérieure à la norme de f frottement (F>400 N) translation rectiligne freiné: la vitesse diminue la force motrice a une norme inférieure à la norme de f frottement (F<400 N)
|
||||||
|
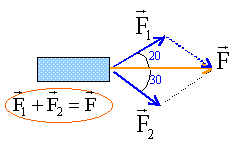
Un traîneau est tiré, en mouvement de translation rectiligne, sur une surface enneigée horizontale par deux chiens. Chaque chien est relié par une corde au traîneau. Les cordes, attachées en un même point O à l'avant du traîneau, restent dans un plan horizontal. L'une des cordes (corde1) fait un angle a =20° avec l'axe du traîneau, l'autre (corde2) un angle b=30°. La résultante vecteur F des forces F1 et F2 exercées par les cordes 1 et 2 sur le traîneau est portée par l'axe du traîneau et vaut 300N.
corrigé forces agissant sur le traîneau (frottement négligés) poids et action normale du sol Rn sont deux vecteurs opposés.
schéma en vue de dessus :
en projection sur l'axe du traîneau : F1 cos 20 + F2 cos 30 = F = 300 0,94 F1 + 0,866 F2 = 300 (1) en projection sur un axe perpendiculaire à l'axe du traîneau : F1 sin 20 - F2 sin 30 = 0 F1 = F2 sin 30 / sin 20 = 1,46 F2 . repport dans (1) : 0,94 (1,46 F2) + 0,866 F2 = 300 F2 = 134 N. F1 =1,46 *134 = 195,6 N. le premier chien exerce un effort supérieur au second chien
|
||||||
|
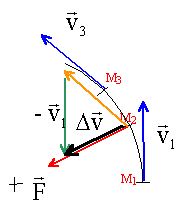
Ganymède, identifié en 1610 par galilée, est une lune de Jupiter. Sa trajectoire autour de Jupiter est quasiment circulaire de rayon r = 1,07 106 km. Sa période de révolution autour de Jupiter est T= 7,15 jours. Sa masse (m= 1,5 1023 kg) est petite devant celle de Jupiter M= 1,9 1027 kg.
corrigé 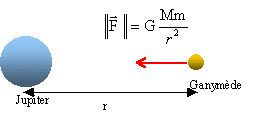
distance en m : r = 1,07 109 m F= 6,67 10-11* 1,9 1027 *1,5 1023 / (1,07 109)² = 1,66 1022 N. la période doit être exprimée en seconde : T= 7,15 *24*3600 = 6,18 105 s circonférence de la trajectoire de Ganymède : 2p r 2*3,14*1,07 109 = 6,72 109 m. vitesse = 6,72 109 / 6,18 105 = 1,087 104 m/s.
le vecteur variation de vitesse est colinéaire au vecteur force de gravitation.
|
||||||
|
On considère, à la surface de la Terre, un repère orthonormal (O,i, j). Le vecteur j est vertical, dans le sens ascendant. On fixe deux charges ponctuelles de même valeur q positive aux points de coordonées (-a,O) et (+a,0). On place un objet M, de charge q et de masse m,au point de coordonées (O,y)
corrigé Le solide M est soumis à 3 forces : poids P=mg, vertical vers le bas forces de Coulomb ( deux charges de même signe se repoussent ) A l'équilibre la somme vectorielle des forces est nulle. tan a = 3a/a = 3
Si M porte la charge -q, alors M se trouve du coté des y négatif tel que y = -3a Deux charges de signe contraire s'attirent ; les forces de Coulomb sont toujours dirigées vers le haut comme sur la figure.
|
||||||
|
Un cylindre en aluminium de hauteur h=20 cm de diamètre D= 2,0 cm est suspendu à un dynanomètre. La masse volumique de l'aluminium est 2,7 g/cm3. On néglige la poussée d'Archimède due à l'air. Le centre de gravité G du cylindre est son centre de symétrie.
corrigé Dans l'air, le dynamomètre mesure le poids du cylindre
d'aluminium. poids : 0,169*9,8=1,66 N. la poussée
d'archimède : verticale, vers le haut, valeur : F = V reau g =62,8 10-6
*1000*9,8 =0,615 N
|
||||||
| |
||||||
| |
||||||
| |
||||||
|