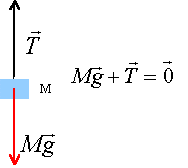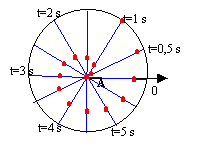
A se trouve au centre d'un manège de rayon R=7 m tournant à vitesse constante de 10 tr/min. L'enfant A s'eloigne du centre et se dirige en ligne droite sers le bord à vitesse constante V par rapport au manège : V = 1 m/s.

1. Dans un référentiel lie au manège, quelle est la trajectoire de l'enfant ?
   - representer les positions de l'enfant toutes les 0,5 s ( échelle 1 m pour 1 cm)
2. Dans un référentiel lié au sol, calculer l'angle dont tourne le manège en 0,5 s.
   - représenter le position de l'enfant toutes les 0,5 s. Quelle est la nature de la trajectoire ?
3. Au bout de combien de temps arrive-t-il a l'extrémite du manège ?
   - De quel angle a alors tourné le manège ?

Deux trottoirs roulants parallèles, de 50 m de long, avancent en sens contraires à la vitesse constante de 3 km/h par rapport au sol. A l'instant t=0, trois personnes s'engagent dans le bon sens sur les trottoirs:

- Alain monte sur le trottoir T₁ et marche à la vitesse constante Va=5 km/h par rapport à ce trottoir

-Bernard monte sur le trottoir T₂ et s'arrête de marcher ;

-Carole monte sur le trottoir T₂ et marche à la vitesse constante Vc=4 km/h par rapport à ce trottoir.

1. A quel instant Alain et Bernard quittent-ils leurs trottoirs roulants?
2. A quel instant Alain croise-t-il Bernard?
3. A quel instant Alain croise-t-il Carole? Quelle distance Carole a-t-elle alors parcourue sur le trottoir T₂?

oxydo-réduction :

Une solution d' éthanol notée A a été préparée en dissolvant une certaine quantité de matière n0 moles d'éthanol pur dans de l'eau de façon à obtenir 1L de solution On prélève 10 cm3 de cette solution A on effectue son oxydation complète par une solution B de dichromate de potassium , acidifiée par de l'acide sulfurique, en excès : on utilise 30 cm3 de cette solution B de concentration 0,1 mol/L

3 C₂H₆O + 2 Cr₂ O₇ ^2- + 16 H⁺ --> 3 C₂ H₄ O₂ +11 H₂O + 4 Cr³⁺.

On dose l'excès d'ions dichromate par une solution C de sulfate de fer II de concentration 0,1 mol/L. Il faut verser 61,2mL pour atteindre l'équivalence. (les quantités de matière des réactifs sont stoéchiométriques à l'équivalence)

Cr₂ O₇ ^2- + 6Fe²⁺ + 14 H⁺--> 2 Cr³⁺ + 7 H₂O + 6 Fe³⁺.

1. Etablir le tableau d'évolution de la réaction du dosage du dichromate par les ions fer II.
2. Calculer la quantité de matière initiale d'ion dichromate et en déduire la quantité de matière d'ion dichromate ayant réagi avec l'alcool.
3. Etablir le tableau d'évolution de la réaction d'oxydation de l'alcool et en déduire la concentration de l'alcool dans A.
4. Le degré alcoolique est égal à la mesure du volume exprimée en mL, d'alcool pur contenu dans 100 mL de ce mélange eau alcool. Calculer le degré alcoolique de la solution A.

Masse volumique éthanol 0,790g/ml

Masse molaire en g/mol : C=12 ; H=1 ; O=16; éthanol C₂H₆O.

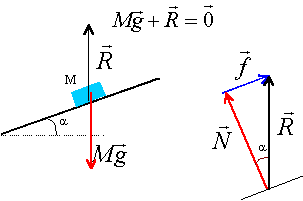
ressort:

Un ressort à spires non jointives a une longueur à vide l₀= 20cm et une constante de raideur k= 25 N/m. Son extrémité supérieure est fixe ; un objet de masse m = 100 g est accrochée à son extrémité inférieure. Quelle est sa longueur ? g= 10 N/kg.

action du plan incliné :

Un bloc cubique de masse m= 200 kg est immobile sur un plan incliné d'un angle a=20° sur l'horizontale. Le coefficient de frottement entre le bloc et le plan est 0,5.

1. Faire un schéma à l'échelle.
2. Déterminer à l'aide du schéma et par le calcul les normes des composantes normale et tangentielle de l'action du support.
3. Le bloc peut-il être immobile ?