|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||
|
||||||
|
|
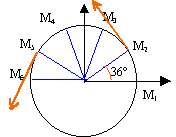
La figure suivante est la reproduction à 1/10ème du mouvement du centre d'un mobile autoporteur attaché en O fixe sur une table horizontale. L'intervalle de temps séparant deux marques consécutives vaut t=80ms. 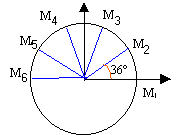 Distance entre chaque point : 2,2 cm ; tous les angles sont identiques; rayon du cercle R= 3,5 cm.
corrigé |
|||||
|
v2 : calcul d'une vitesse moyenne sur le parcours M1M3 distance M1 M3 : 4,4 cm = 4,4 10-2 m temps 160 ms = 0,16 s v2 = 4,4 10-2 / 0,16 = 2,2 / 8 = 0,275 m/s en tenant compte de l'échelle : 2,75 m/s. rayon 3,5 cm = 0,035 m vitesse angulaire =v2 / rayon = 0,275 / 0,035 = 7,85 rad/s. diviser par 2 p pour avoir des tours par seconde : 1,25 tr/s soit 1,25 *60 = 75 tours /min. la vitesse angulaire est constante, le mouvement étant uniforme. la norme de la vitesse linéaire est constante, mais la direction (tangentes au cercle)de ce vecteur vitesse change : donc le vecteur vitesse n'est pas un vecteur constant.
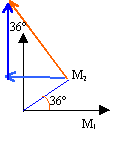
à t2 : abscisse de la vitesse -v2 sin 36 = -1,6 ordonnée de la vitesse v2 cos 36 = 2,2
|
||||||
|
Le propane est commercialisé sous forme liquide: la bouteille contient 7 kg de propane et a un volume de 10L.
corrigé masse volumique : 7 / 10 = 0,7 kg/L = 700 kg/m3 pour le propane liquide masse molaire du propane : C3H8 donc 3*12+8 = 44 g/mol densité par rapport à l'air : 44 /29 = 1,51 masse volumique 1,51 g/L, propane gaz plus lourd que l'air le propane est supposé être un gaz parfait, température 20 °C PV = nRT P= 105 Pa; n = 7000 /44 = 159 mol; T=273+20= 293 K V = 159*8,31*293 / 105 = 3,87 m3 volume auquel il faut retrancher 10 L restant dans la bouteille C3H8 + 5 O2 donne 3 CO2 + 4 H2O 159*5 = 795 mol dioxygène l'air contient 20% en volume de dioxygène 795*5 = 3977 mol d'air fois le volume molaire(24 L/mol à 20°C) volume d'air : 3977 *24 = 95,4 m3. 1L de gaz divisé par le volume molaire 24L/mol = 41,6 mmol propane donc 41,6*4 = 0,166 mol eau fois masse molaire 18 g/mol donne 3 g d'eau ou 3 mL d'eau .
|
||||||
|
vin : Un résidu de 10 mL de vin à 11° ( 11 g d'alcool pur pour 100 mL de vin ) est abandonné dans une bouteille de 750mL bouchée. En s'oxydant, le vin se transforme en vinaigre. La quantité d'air enfermé dans la bouteille est-elle suffisante pour permette l'oxydation de la totalité de l'alcool du vin ? masse volumique alcool 0,8 g /mL; alcool éthylique C2H5OH masse atomique molaire : C=12 ; H=1; O=16 g/mol ; volume molaire des gaz = 24 L/mol C2H5OH + O2 donne C2H4O2 +H2O corrigé volume d'air 740 mL donc 740 / 5 = 148 mL dioxygène divisé par le volume molaire des gaz 24 L/mol à 20°C 0,148 / 24 = 6,1 mmol dioxygène 11° soit 11 g d'alcool pur dans 100 mL de vin 1,1 g d'alcool pur dans 10 mL de vin masse molaire alcool éthylique : 46 g/mol 1,1 / 46 = 24 mmol d'alcool C2H5OH + O2 donne C2H4O2 +H2O on ne pourra oxyder que 6,1 mmol d'alcool en vinaigre.
|
||||||
|
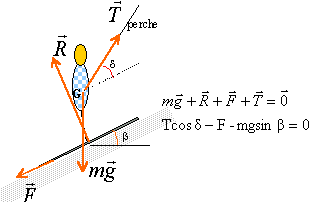
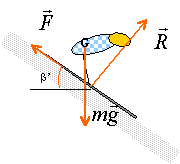
force: Cet exercice étudie un modèle très simplifié du mouvement du centre d'inertie G d'un skieur. Masse du skieur m= 80 kg. Montée: L'ensemble des forces de frottement est assimilé à une force unique, de sens opposé au vecteur vitesse, de norme constante F=50N. Le skieur reste constamment en contact avec le sol. Le skieur toujours tiré par la perche, monte à vitesse constante (2m/s) une pente rectiligne inclinée de b=40° par rapport à l'horizontale. La perche forme un angle d=30° avec le sol. Après avoir schématisé le skieur, déterminer littérallement puis numériquement l'intensité de la force T exercée par la perche sur le skieur. descente : Le skieur participant à un concours de vitesse, s'élance, à partir du repos sur une piste rectiligne inclinée de b'= 28° par rapport à l'horizontale. En admettant l'existence de force de frottement de même valeur qu'à la montée, représenter les forces agissant sur le skieur.
D'après le principe d'inertie la somme des forces est nulle. projection suivant un axe parallèle au plan vers le haut
T = (F+mgsinb) / cosd. T=(50+80*9,8*sin40) / cos30 = 639 N.
|
||||||
| |
||||||
|