Aurélie oct 2001

devoirs en première S

eau oxygénée

synthèse de l'ammoniac

dipole

Jupiter

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



Google


.
.

 L'eau oxygénée se décompose lentement suivant la réaction : H2O2 --> H2O + ½O2. Un litre d'eau oxygénée à 10 volumes signifie que la décomposition complète de l'eau oxygénée libère 10 L de dioxygène.

  1. Quel est le volume de dioxygène libéré par la décomposition complète de 25 mL d'eau oxygénée à 10 volumes?
  2. A quel quantité de matière n1 cela correspond -il à 20°C sous la pression de 105 Pa.
  3. Dresser le tableau d'avancement de ce système.
  4. En déduire la quantité initiale n0 de H2O2 et sa concentration.
  5. Si le volume de 25 mL d'eau oxygénée est dans un flacon bouché de volume total 100 mL, quelle sera la pression finale dans le flacon lorsque toute l'eau oxygénée sera décomposée ( la pression initiale est la pression atmosphérique). On admet que le volume du liquide ne varie pas.
corrigé
1L = 1000 mL d'eau oxygénée à 10 volume libère 10 L de dioxygène

25 mL libèrent : 10*25/1000 =0,25 L de dioxygène.

équation des gaz parfaits : PV = nRT

P= 105 Pa ; V= 0,25 L = 2,5 10-4 m3 ; T= 273+20=293K; R= 8,31 SI

n1 =105 *0,25 10-3 / (8,31 *293) = 10,27 mmol.

H2O2
--> ½ O2
+ H2O
initial
n0 mmol
0
0
en cours
n0 - x
0,5 x
x
fin
0
10,27 mmol
2*10,27 = 20,54 mmol
0,5 x max= 10,27 donne xmax=20,54 mmol.

n0 - xmax = 0 d'où n0 = 20,54 mmol.

20,54 mmol contenu dans 25 mL

d'où [H2O2]= 20,54 / 25 =0,821 mol/L

état initial :

volume d'air au dessus du liquide : 75 mL = 0,075 L = 7,5 10-2 L = 7,5 10-5 m3.

P= 105 Pa; T=293 K; R=8,31 SI.

qté de matière d'air: n= 105 * 7,5 10-5 /(8,31*293)= 3 mmol

état final :

3 mmol d'air et 10,27 mmol de dioxygène = 13,27 mmol = 13,27 10-3 molde gaz

volume : 75 mL = 7,5 10-5 m3

T=293K

P= 13,27 10-3*8,31 *293 / 7,5 10-5 = 4,3 105 Pa.

 On réalise la synthèse de l'ammoniac NH3 à partir du dyihydrogène H2 et du diazote N2.

  1. Ecrire l'équation de la réaction
  2. On utilise 48 L de dihydrogène et 96 L de diazote ( volume molaire =24 L/mol). 2tablir le tableau d'avancement de la réaction.
  3. Déterminer la valeur de l'avancement maximal.
  4. La réaction étant réalisée à volumee V0 constant, exprimer à l'état initial, la pression P0 du mélange en fonction de la températureT.
  5. Donner l'expression de la quantité de matière totale n, des gaz lorsque l'avancement est x.
  6. Exprimer la pression P du mélange gazeux lorsque l'avancement est x. Montrer qu'il existe une fonction affine entre P et x. Tracer le graphe de cette fonction.

Qtés de matière initiales :

H2 : 48/24 = 2 mol

N2 : 96 /24 = 4 mol
3 H2
+ N2
--> 2 NH3
initial
2 mol
4 mol
0
en cours
2 - 3 x
4- x
2 x
fin
0
4-0,666 = 3,333 mol
1,333 mol
la réaction est terminée lorsque l'un au moins des réactifs a disparu.

2- 3x max= 0 donne xmax=0,6666 mol.

ou bien 4- xmax= 0 soit xmax= 4 mol.

état initial : 6 mol de gaz

V0 = 48+96 = 144 L = 0,144 m3.R=8,31 SI.

équation des gaz parfaits : PV = nRT

P0 = n0RT/V0 = 6*8,31 T / 0,144 = 346,2 T.

quantité de matière des gaz lorsque l'avancement est x :

2-3x + 4-x +2x = 6 -2x mol

pression du gaz à la date t:

P= nRT / V0 avec RT/V0 = P0 / n0

P= (6-2x) P0 / n0 = - 2xP0 / n0 +6 P0 / n0

fonction affine décroissante; droite de coefficient directeur -2P0 / n0



dipôle :

Un dipôle est formé de deux charges ponctuelles +q et -q situés en deux points A et B tels que AB=2a. Un ion négatif portant la charge -e est disposé en un point P de la médiatrice de [AB], à la distance d du milieu O du segment [AB].

  1. Quelles sont les forces électrostatiques qui agissent sur le dipôle AB?
  2. Représenter ces forces sur un schéma.
  3. Donner l'expression littérale de ces forces.Quel est l'effet de ces forces sur le dipôle AB, s'il est déformable?
corrigé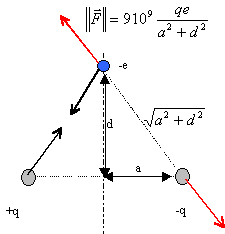

le dipôle va tourner, présenter son pôle positif en regard de la charge négative, puis être attirer par cette charge négative.

Jupiter:

Les sondes Voyager 1 et 2 avaient pour mission d'explorer le système solaire. La masse de chaque sonde était de 815 kg. Le 5 mars 1979 Voyager 1 s'approcha de Jupiter à l'altitude z1 = 278 000 km et mesura une force gravitationnelle exercée par la planète F1=845 N. Quelques mois plus tard, Voyager 2 ne s'approcha qu'à l'altitude z2 = 650 000 km de cette planète et mesura une force gravitationnelle F2 = 198 N.

  1. Donner les expressions des forces en notant M, la masse de Jupiter et R le rayon de cette planète.
  2. Exprimer R en fonction de z1, z2, F1, F2. Calculer R
  3. En déduire la masse de Jupiter.G= 6,67 10-11 SI.
corrigé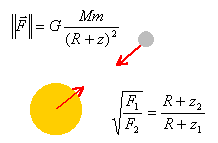

application numérique : (845 / 198 ) ½ = 2,065

2,065R + 2,065 *2,78 108 = R+ 6,5 108.

1,065 R = 7,6 107.

R= 7,1 107m = 7,1 104 km.

masse de Jupiter :

M= F1 (R+z1)² / (Gm) = 845 *(0,71 + 2,78)² 1016 /(6,67 10-11*815)=1,9 1027 kg.



à suivre ...
retour - menu
à bientôt ...