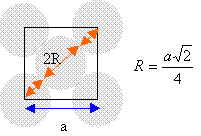Aurélie sept 2001
cristallochimie

à propos de l'aluminium (Capes 73)

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


I aluminium

L'aluminium cristallise dans le système cubique à faces centrées.

  1. Calculer la compacité de ce système (on appelle compacité le rapport entre la somme des volumes des atomes appartenant à la maille et le volume de cette maille, les atomes étant supposés sphèriques).
    arète de la maille : 2a =4,041 10-10m. Al = 26,98 g/mol
  2. Montrer que la compacité du système hexagonal compact a même valeur.
  3. Calculer la masse volumique de l'aluminium.
corrigé
La maille de ce système est un cube ayant un atome à chacun des huit sommets et un atome au centre de chaque face.

chaque atome situé sur un sommet appartient à huit mailles et contribue pour 1 /8 éme à la maille.

chaque atome situé au centre d'une face appartient à deux mailles et contribue pour ½ à la maille.

il y a donc 3+1 = 4 atomes par maille.

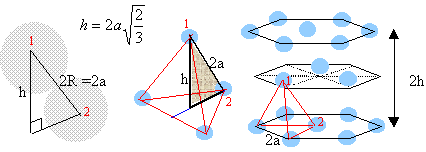
volume de la maille: a3.

volume des quatre atomes : 4 *(4/3*3,14* R3) = 3,14 a3 / (3*1,414)

compacité : 3,14 / (3*1,414) = 0,74.

La maille du système hexagonal compact est un prisme droit à base hexagonale avec un atome à chacun des douze sommets, trois atomes dans le plan méridien et un atome au centre de chaque base.

chaque atome situé à un sommet appartient à 6 maille et contribue pour 1/ 6 ème à la maille

chaque atome situé dans le plan méridien appartient à une seule maille.

chaque atome situé au centre des bdeux bases appartient à deux maille et contribue pour ½ à la maille.

donc 12/6 +3 +2*½ = 6 atomes par maille.

volume de la maille : surface hexagone de coté 2a fois la hauteur 2h.

surface hexagone = 6 fois surface d'un triangle équilatéral de coté 2a

volume = 24*1,414*a3

volume des atomes : 6 *( 4/3 *3,14 *a3)

compacité : 3,14 / (3*1,414 )= 0,74.

masse volumique de l'aluminium :

masse des atomes contenus dans une maille :

6,023 1023 atomes ont une masse de 26,98 g (masse molaire aluminium)

4*26,98 / 6,023 1023 = 1,79 10-22 g = 1,79 10-25 kg

volume de la maille (2a)3 = (4,041 10-10 )3= 6,6 10-29 m3.

masse volumique : 1,79 10-25 / 6,6 10-29 = 2712 kg m-3.

II alun d'aluminium et d'ammonium Al2(SO4)3, (NH4)2 SO4, 24 H2O.

  1. Donner la formule d'un autre alun d'aluminium
  2. Donner la formule de deux autres aluns autres que ceux d'aluminium.

III spinelle de magnésium :

  1. Faire le croquis d'une maille du réseau cubique à faces centrées; préciser les positions et nombre de sites tétraédriques et des sites octaédriques.
  2. Le spinelle de magnésium présente un réseau d'ions O2- définissant un système cubique à faces centrées dans lequel les ions Mg2+ occupent un huitième des sites tètraèdriques et les ions aluminium Al3+ la moitié des sites octaèdriques; Définir la formule du spinelle de magnésium.
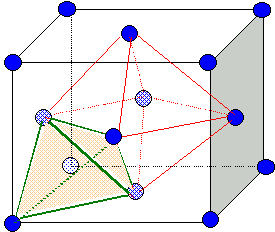
corrigé
Les aluns sont des sulfates doubles hydratés de formule générale :

M2(SO4)3, N2 SO4, 24 H2O.

avec M : Al, Ga, V, Cr, Fe, In, Rh.

et N : K, NH4, Rb, Cs.

formule d'un autre alun d'aluminium:

Al2(SO4)3, K2 SO4, 24 H2O.

formules de deux autres aluns:

Ga2(SO4)3, Rb2 SO4, 24 H2O.

Fe2(SO4)3, (NH4)2 SO4, 24 H2O.

site tétraèdrique : les sommets du tétraèdre sont constitués par un sommet du cube et trois atomes au centre de trois faces ayant ce sommet en commun.

Il y a huit sites tétraèdriques.

site octaèdrique :octaèdre. Il y en a 4 par maille; ils sont situés au centre de la maille et aussi au milieu des arètes.

 

spinelle de magnésium :

par maille il y a 4 ions O2-, un ion Mg2+ et deux ions Al3+.

La maille est électriquement neutre: la formule du spinelle est :

MgAl2O4 ou MgO, Al2O3.

 

retour - menu