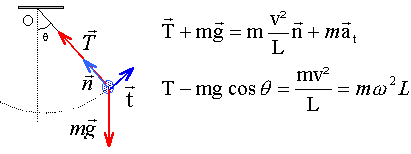En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

Données : Rayon de la terre : R=6400 km ; g_z / g₀ = 1 - 2z /R. On admet que : (1+ e)0,5 = 1+0,5e. pour e petit devant 1.

Montrons que l₀=1 m.

période du pendule T= 2p racine carrée (l₀/g)

d'où l₀ = T² g / (4p²) = 4*10 / (4*3,14²) = 1 m.

Exprimons puis calculons la nouvelle longueur l₁ lui permettant de conserver sa période propre T₀.

longueur à l'altitude z = 64 km :

g₀ = GM/R² ( R rayon de la Terre ; M :masse de la Terre ) soit GM=g₀ R²

à cette altitude g =GM/(R+z)² = g₀ R²/(R+z)² = g₀/[1+(z/R)]²

or z/R <<1 d'où : g₀/[1+(z/R)]² proche de g₀(1-2z/R)

g_z = g₀ ( 1 - 2z /R) = 10*(1 - 2*64 / 6400) = 9,8 m/s².

l_z = T² g_z / (4p²) = 4*9,8 / (4*3,14²) = 0,98 m.

La longueur est de nouveau l₀=1m. Calculons l'altitude z à laquelle se trouve le pendule pour que sa période propre augmente de 0,01 s.

période T= 2,01 s à l'altitude z :

T = 2,01 s ; l₀ = 1m ; T= 2p racine carrée (l₀/g_z)

g_z = 4p² l₀ /T² = 4*3,14²*1 / 2,01² = 9,76 m/s²

de plus g_z = g₀ ( 1 - 2z /R)

d'où : 1- 2z /R= g_z / g₀ soit (1 -g_z / g₀ )R = 2z

z = ½( 6400) ( 1 - 9,76 /10) = 76,8 km.

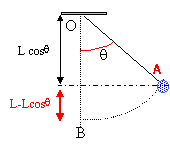
écrire le théorème de l'énergie cinétique entre le départ A et l'arrivée B.

seul le poids travaille (la tension du fil est constamment perpendiculaire à la vitesse)

le travail du poids est résistant lors d'une montée :

W( poids )A-->B = -mg h = - mg L(1 -cosq)

variation d'énergie cinétique : 0- ½mv²_B avec v_B = w₀ L = 1 m/s

- ½mv²_B = - mg h soit h = v²_B / (2g) = 1 / 20 = 0,05 m.

h = L-L cos q d'où cosq = 0,95 et q = 18,2°.

écrire la seconde loi de Newton dans la base de Frenet :

q = 0 alors T = m(g + w₀²L )

T = 0,2(10+1) = 2,2 N.

q = 18,2° alors T = m(g cos 18,2+ w²L )

T = 0,2(10*0,95+0) = 1,9 N.