Aurélie 09/11/06
 

physique chimie ( d'après concours interne 2002 ) Détermination de la résistance R d'un conducteur ohmique par une méthode calorimétrique
. .


 

Web

www.chimix.com

On dispose d'un calorimètre dont l'ensemble cuve et accessoires a une capacité thermique Cth=120 J K-1. On verse dans le calorimètre un volume d'eau tiède de valeur V= 100,0 mL, et après quelques minutes, on mesure la température qi=17,0°C. On pèse un bloc de glace ( mg= 88,7 g) pris à la température qg=-20,0°C et on le plonge dans l'eau contenue dans le calorimètre.

Données : ceau = 4180 J kg-1 K-1 ; cglace =2100 J kg-1 K-1 ; Lfusion = 335 103 J kg-1.

calorimètre :

vase adiabatique ( pratiquement pas d'échange avec le milieu extérieur)

paroi interne brillante (en verre) limitant le rayonnement

vide entre les doubles parois : pas de convection

parois externe isolante : pas de conduction

A l'équilibre thermique la température à l'intérieur du calorimètre vaut qéq=0,0°C :

hypothèse : toute la glace glace fond à 0°C et la température finale est 0°C.

énergie gagnée par la glace pour se réchauffer de -20 °C à 0°C sans fondre :

Q1 = mg cglace(0-qg)= mg cglaceqg=88,7 10-3*2100*20 = 3725 J

énergie gagnée par la glace pour fondre à °C : Q2 = mgLfusion =88,7*335 = 29714 J

Q1 + Q2 = 3725 + 29714 = 33439 J

Energie cédée par les corps chauds, eau ( 100 g = 0,1 kg) et calorimètre :

Q3= (0,1ceau + Cth)(0-qi) = (0,1*4180+120)*(-17) = - 9146 J

Or |Q3| < Q1 + Q2 donc toute la glace ne peut fondre ; cette hypothèse est fausse.

hypothèse : une masse m1g de glace fond à 0°C.

3725 J sont nécessaire pour réchauffer 88,7 g de glace de -20 à 0°C ; il reste donc : 9146-3725 = 5421 J pour faire fondre une masse m1g de glace à 0°C

5421 = m1g Lfusion ; m1g = 5421 / 335 103 = 16,2 g.

dans le calorimètre à l'équilibre thermique : masse d'eau m'= 100+16,2 = 116,2 g ; masse de glace m'g = 88,7-16,2 = 72,5 g.

Le mélange final contient de l'eau et de la glace : sa température est 0°C.

 

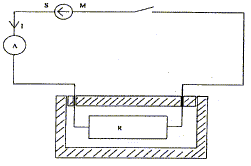
On plonge ensuite le conducteur ohmique R dans le liquide et on réalise le circuit suivant :

A la date t=0, on ferme le circuit et on mesure I= 294 mA. A la date t= 7 min 11s, on constate la disparition totale de la glace. En précisant les hypothèses faîtes pour le bilan énergétique, déterminer la valeur de R.

 

Energie nécessaire pour faire fondre une masse m'g = 72,5 g de glace à 0 C : Q4 = m'gLfusion =72,5*335 = 24287 J

Energie fournie par effet joule : Q= RI²t avec I= 0,294 A et t = 421 s.

Q4 =Q soit R= m'gLfusion /(I²t) = 24287/(0,2942*431) = 652 W.

Cette dernière méthode est sans doute la plus précise.

Pour la première, les constantes de temps sont peu précises ; pour la seconde r et K sont peu précises.

Estimation numérique de l'incertitude relative sur la valeur de R :

log R= log m'g + log Lfusion - 2 log I-log t

d'où DR/R= Dm'g/m'g + 2DI/I + Dt/t = 0,1/75,2 + 2/294 + 1/431 voisin de 10-2 ( 1%)


retour -menu