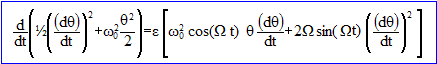physique chimie ( d'après concours 2000) La résonance paramétrique

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

On considère un pendule simple de longueur variable l(t), réalisé à l'aide d'un fil inextensibleMON coulissant à travers d'un anneau en O. Son extrémité N est animée d'un mouvement sinusoïdal de faible amplitude de sorte que : OM(t) = l(t)=l0(1+e cos(Wt)) avec e <<1. On agit ansi périodiquement sur la longueur OM du pendule

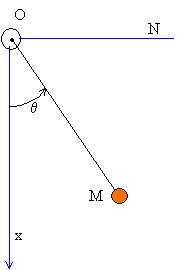
(1) : j'exprime le moment cinétique

La masse m est soumise à deux forces : la tension du fil et son poids :

(2) Le moment, par rapport à O, de la tension est nul : cette force rencontre le point O.

(3) : j'exprime le moment en O du poids.

(4) : j'applique le théorème du moment cinétique
En appliquant le théorème du moment cinétique, j'établis l'équation différentielle du mouvement :

(4) donne l'équation différentielle vérifiée par l'angle q(t) en fonction du temps : q " + 2l '/l q '+ g /l sin q = 0.

or e <<1 d'où 1/ l = 1/(l₀(1+e cos(Wt))) proche de : (1-e cos(Wt))/l₀

d'où :q " -2 e W sin(Wt)(1-e cos(Wt)) q '+ g /l₀ (1-e cos(Wt)) sin q = 0.

pour les petites oscillations q proche sin q ; et en posant w₀²=g/ l₀, on obtient l'équation :

q " + w₀² q - (1-e cos(Wt)) [ 2 e W sin(Wt) q ' ]- w₀² q e cos(Wt) = 0.

Développer en négligeant le terme en e² : q " + w₀² q -2 e W sin(Wt) q ' -w₀²eq cos(Wt)=0

q " + w₀² q = e[2W sin(Wt) q ' + w₀²q cos(Wt)]

en multipliant chaque terme par q ' : q " q ' +w₀² q q ' = e[2W sin(Wt) q '² + w₀²q q ' cos(Wt)]

Or q " q ' + w₀² q q ' =d/dt[½q '²+ ½w₀²q²]

d'où :

Par une approche énergétique on peut déterminer la condition de résonance :

Un solution approchée de l'élongation angulaire q(t) peut se mettre sous la forme : q(t) =A(t) cos (w₀t+j).

q ' = -Aw₀sin (w₀t+j) + A' cos (w₀t+j).

La variation de A(t) avec le temps étant faible, on peut écrire dA/dt<<w₀A/(2p) : d'où q ' = -Aw₀sin (w₀t+j)

repport dans [ ½q '²+ ½w₀²q²] :

½A²w₀²sin² (w₀t+j) +½A²w₀²cos² (w₀t+j) = ½A²w₀²

par suite : d/dt [ ½q '²+ ½w₀²q²] = ½w₀²dA²/dt = e[2W sin(Wt) q '² + w₀²q q ' cos(Wt)]

avec q =A(t) cos (w₀t+j) et q ' = -Aw₀sin (w₀t+j) , d'où :

½w₀²dA²/dt = e[2A²w₀²W sin(Wt) sin² (w₀t+j) - w₀³A² cos (w₀t+j)sin (w₀t+j) cos(Wt)]

or cos (w₀t+j)sin (w₀t+j) = ½ sin (2w₀t+2j) et 2sin² (w₀t+j)= 1-cos (2w₀t+2j)

par suite : ½w₀²dA²/dt = ½ eA²w₀² [2W sin(Wt)(1-cos (2w₀t+2j)) - w₀ sin (2w₀t+2j)cos(Wt)]

de plus : sin(Wt)cos (2w₀t+2j) = ½[sin(Wt+2w₀t+2j )+ sin(Wt-2w₀t-2j )]

et sin (2w₀t+2j)cos(Wt) = ½[sin(Wt+2w₀t+2j )+ sin(2w₀t+2j-Wt )]

en conséquence : ½w₀²dA²/dt = ½ eA²w₀² [2Wsin(Wt) -W(sin(Wt+2w₀t+2j )-W( sin(Wt-2w₀t-2j ))-½ w₀(sin(Wt+2w₀t+2j )+ sin(2w₀t+2j-Wt ))]

or sin(2w₀t+2j-Wt ) = -sin(Wt-2w₀t-2j )

½w₀²dA²/dt = ½ eA²w₀² [2W( sin(Wt)-( ½ w₀+W) sin(Wt+2w₀t+2j )- ( ½ w₀-W)sin(Wt-2w₀t-2j )]

dA²/dt = e A² [2W( sin(Wt)-( ½ w₀+W) sin(Wt+2w₀t+2j )- ( ½ w₀-W)sin(Wt-2w₀t-2j )]

On suppose de plus que l'énergie mécanique E est proportionnelle au carré A² de l'amplitude A.

E= kA² avec k une constante ; dE²/dt= 2EdE/dt = kdA²/dt

2EdE/dt = e E² [2W( sin(Wt)-( ½ w₀+W) sin(Wt+2w₀t+2j )- ( ½ w₀-W)sin(Wt-2w₀t-2j )]

soit :

Calcul de la moyenne de 1/E dE/dt :

W différent de 2w₀ :

la moyenne d'une fonction sinus est nulle : dE/E est nulle ; l'énergie mécanique de l'oscillateur est constante.

W égal à 2w₀ :

1/EdE/dt = e [2W( sin(Wt)- 2,5 w₀ sin(4w₀t+2j )]

<sin(Wt)> = 0 ; <sin(4w₀t+2j )>= sin (2j)

<1/EdE/dt>=e 2,5 w₀ sin (2j)= b= constante

<dE/dt>= b <E> ; solution du type : <E> = e^bt.

L'énergie croît exponentiellement. C'est le phénomène de résonance paramétrique.