Physique chimie : fibre optique ; étude du prisme.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

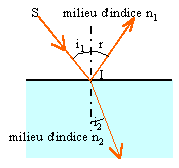
Les trois rayons incident, réfléchi et réfracté sont dans le même plan ; l'angle d'incidence i₁ est égal à l'angle de réflexion r. Les angles d'incidence i₁ et réfracté i₂ sont reliés par la relation : n₁ sin i₁ = n₂ sin i₂.

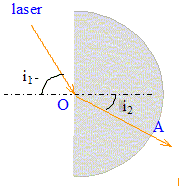
Le rayon incident doit passer par le centre O du demi-cercle : dans ces conditions le rayon réfracté OA est perpendiculaire en A au dioptre plexiglas/air, et en conséquence n'est pas dévié en A. On mesure l'angle d'incidence i₁ et l'angle réfracté i₂.

On peut tracer les courbes i₂ = f(i₁) ou mieux sin i₁ = f( sin i₂) : le graphe de cette dernière est une droite passant par l'origine et dont le coefficient directeur est égal à l'indice de réfraction du plexiglas. ( n _air sin i₁ = n_plexi sin i₂ ; n_plexi = sin i₁ / sin i₂)

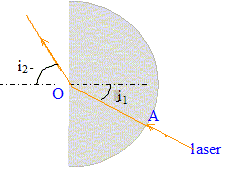
Si la lumière arrive sur la face courbe suivant l'un des rayons du demi-cylindre ( On s'intéresse à la réfraction sur le dioptre plexiglas-air), on peut mettre en évidence le phénomène de réflexion totale. Expression de l'angle limite i_lim à partir duquel apparaît ce phénomène :

en O : n_plexi sin i₁ = n _air sin i₂ ; n_plexi sin i₁ = sin i₂ et |sin i₂| inférieur ou égal à 1.

n_plexi sin i_lim = 1 soit sin i_lim = 1/ n_plexi .

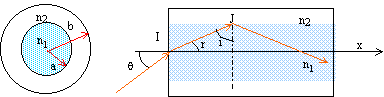
Un rayon laser se propageant dans l'air dans un plan contenant l'axe de la fibre pénètre dans le coeur de la fibre. Le rayon incident au point I reste dans le coeur si l'angle q_i d'incidence à l'entrée de la fibre est inférieur à un angle a que l'on va calculer :

en I, dioptre air/coeur : n_air sin q_i = n₁ sin r ; sin q_i = n₁ sin r (1)

en J, il y a réflexion totale : dioptre coeur/gaine : n₁ sin i = n₂ sin 90 = n₂ ; sin i = n₂ /n₁ = 1,485 / 1,500 = 0,99 ; i = 81,89

les angle i et r sont complémentaires soit sin r = cos i = cos 81,89 = 0,141

de plus (1) s'écrit : sin a = n₁ sin r = 1,5*0,141 =0,212 ; a = 12,2°.

Expression de l'ouverture numérique en fonction des indices n₁, n₂ :
On appelle ouverture numérique de la fibre la quantité sin a.

sin a = n₁ sin r ; de plus sin r = cos i et sin i = n₂ /n₁ ;cos²i + sin²i = 1

par suite cos i = (n₁²-n₂²)^½ / n₁ ; sin a =(n₁²-n₂²)^½ = (1,5²-1,485²)^½ = 0,212.

Expression de la distance d parcourue par la lumière en fonction de son angle d'incidence q_i et de la longueur de la fibre L :

Figure ci-dessus, expression de IJ : ( on note h la projection de IJ sur l'axe de la fibre)

cos r = h/IJ; or sin q_i = n₁ sin r ; cos² r + sin² r = 1 ;

h²/IJ² +( sin q_i / n₁ )² = 1 ; h/IJ = [1-( sin q_i / n₁ )² ]^½.

Le rapport entre la longueur L de la fibre et le trajet d suivi par la lumière est : L/d =[1-( sin q_i / n₁ )² ]^½

d = L[1-( sin q_i / n₁ )² ]^-½.

Encadrement de d si la valeur q_i est comprise entre 0 et 12° et si la fibre a une longueur L= 100 km :

Un faisceau lumineux incident arrivant dans les mêmes conditions que précédemment sur la fibre optique est formés de rayons qui font un angle q_i compris entre 0 et 12 ° avec l'axe de la fibre.

pour q_i =0 , d₀ =100 km ; pour q_i =12 , d₁₂ =100 [1-(sin12/1,5)²]^-½=101 km
La fibre reçoit une très brève impulsion lumineuse, la durée t du signal à la sortie est :

célérité de la lumière dans le coeur d'indice n₁ = 1,5 : v = 3 10⁸/1,5 =2 10⁸ m/s.

durée du signal à la sortie t = 1000/ 2 10⁸= 5 10^-6 s.

Si l'on souhaite transmettre une suite de 0 ( la source lumineuse envoie un très bref éclair puis attend une durée T) et de 1 ( pas de lumière pendant la durée T), quelle est la fréquence maximale de transmission d'une ligne de longueur 100 km ?

Il ne faut pas que deux signaux consécutifs se superposent à la sortie d'où la fréquence maxi : 1/ 5 10^-6 = 2 10⁵ Hz.
Deux applications des fibres optiques :

Les télécommunications, pour la réalisation de réseaux hauts débit : image, son, texte sont d'abord codés en binaire avant transmission ( le 0 correspond à un bref éclair, le 1 correspond à une brève extinction)

En chirurgie, la fibre optique associée à un faisceau laser permet de pulvériser un calcul, détruire une tumeur. De plus en endoscopie, elle éclaire l’intérieur du corps permettant la transmission d' images au médecin.

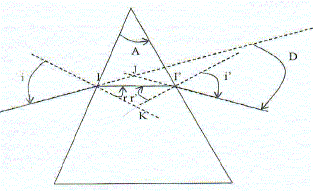
Les lois de Descartes relatives à la réfraction en I et I' :

en I : n_air sin i = n sin r soit sin i = n sin r (1)

en I' : n sin r' =n_air sin i' soit n sin r'= sin i' (2)

Démonstration géométrique : r+r'=A

L'angle r a pour complément l'angle BII' ( en notant B le sommet du prisme)

L'angle r' a pour complément l'angle BI'I ; d'où r+r'+ angle BII' + angle BI'I= 180°

de plus dans le triangle BII' : A + angle BII' + angle BI'I= 180°

des angles ayant même supplément sont égaux, d'où : r+r'=A

Démonstration géométrique : D=i+i'-A

L'angle D a pour supplément l'angle IJI'

Dans le triangle IJI' :( i-r )+ (i'-r') + angle IJI' = 180 °

par suite D= ( i-r )+ (i'-r') = i+i'-(r+r') = i+i'-A.

Conditions d'émergence :
Pour le rayon émerge en I', il faut que l'angle d'incidence vérifie une certaine condition que l'on va exprimer :

On ne peut avoir réflexion totale qu'en passant d'un milieu d 'indice n à un milieu d'indice inférieur à n. En I', il y a réflexion totale si l'angle r' est supérieur à l'angle limite de réfraction noté l tel que sin l = 1/n.

r' inférieur ou égal à l. Les formules du prisme conduisent à :

r supérieur ou égal à A-l d'où : sin i supérieur ou égal à n sin(A-l).

ce qui impose : 1 >= n sin(A-l) ; 1/n >= sin(A-l)

or sin l = 1/n d'où sin(l)>= sin(A-l)

A <= 2l.
Au dela d'une certaine valeur de A, il n'y a plus d'émergence quelle que soit la valeur de l'angle d'incidence du faisceau.

différencier les 4 équations du prisme

cos i di =dn sin r + n cos r dr (1)

cos i' di' =dn sin r' + n cos r' dr' (2)

dA= dr + dr' (3)

dD = di + di' - dA (4)

pour éliminer di' on ajoute : (1) cosr' + (2) cos r

on remplace dans (4)

si A et n sont constants on retrouve : [dD/di]_{A, n} = 1- cosr' cos i / ( cosr cos i').

si r=r' =½A : sin i = n sin(½A) ; n sin (½A) = sin i' ; cos r = cos r'

par suite [dD/di]_{A, n} = 0 ; on passe par un extrémum ( qui est un minimum) de D.
Au minimum de déviation expressions de r_min, i_min, n=f(D_min,A).

r_min = ½A ; sin i_min = n sin(½A) ; n sin (½A) = sin i' d'où i_min = i'_min

or D= i+i'-A soit D_min = 2i_min -A_min ; i_min =½ ( D_min +A_min )

de plus sin i_min = n sin(½A) d'où : n = sin[½ ( D_min +A_min )] / sin(½A)

Il comporte une partie fixe centrale, sur laquelle est montée un plateau mobile. Il possède de plus une graduation en degrés ( rapporteur), et un vernier afin d'améliorer la précision des mesures d'angle. Utilisé en optique, le goniomètre possède une lunette de visée fixée sur la partie mobile.

Le plateau et la lunette de visée doivent être horizontaux ; placer l'arête étudiée du prisme au voisinage du centre du plateau.

Utilisation du prisme en lumière blanche :
Lorsqu' un faisceau de lumière blanche traverse un prisme on observe un arc en ciel , le bleu étant le plus dévié ; cette observation met en évidence une propriété du prisme : le prisme est un mileiu dispersif pour la lumière blanche.