|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||
| .
. |
|||
|
|||
|
|
|||
|
Un projet consiste à faire pousser des cultures par irrigation sur une ile où l'eau douce n'est accessible qu'en prfondeur par pompage. Pour cela, trente éoliennes vont être mise en place, groupées sur une zône ventée à 1 km de la première habitation. Ces éoliennes arrivent par bateau. Une éolienne de pompage se présente de la façon suivante : 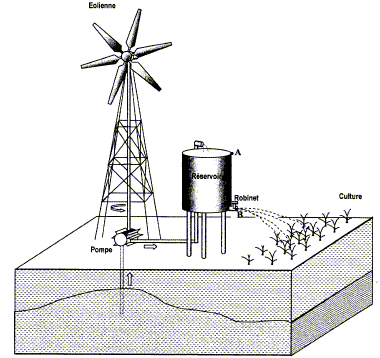
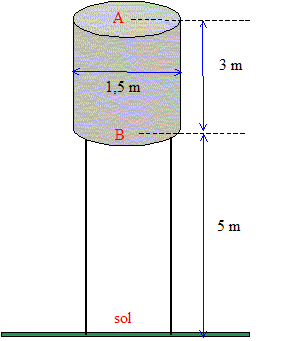
Le réservoir associé à chaque éolienne est ouvert ( pour récupérer éventuellement l'eau de pluie). Il a pour dimensions 1,5 m de diamètre et 3,0 m de hauteur. Son fond est situé à une hauteur de 5,0 m au dessus du sol. Une fois les réservoirs pleins, les pompes sont arrêtées. L'eau va être utilisée pour l'irrigation. Durée de l'irrigation, sans pluie, ni vent : Sachant que les cultures consomment 2 L par plant par jour, qu'il y a 5000 plants, le volume d'eau utile chaque jour est : 2*5000 = 10 000 L = 10 m3. volume d'un réservoir cylindrique : V= pr2h avec r = 0,75 m et h = 3,0 m V= 3,14*0,752*3 = 5,3 m3 volume des 30 réservoirs : 30*5,3 = 159 m3 d'où la durée : 159/10 voisin de
16 jours.
pression PB due au seul liquide en B au niveau du robinet situé en bas du réservoir :
On considère le réservoir suffisamment grand pour que l'eau soit considérée comme stagnante dans le réservoir ( vA=0). La relation de Bernoulli s'écrit : pA + rgzA +½rvA² = pB + rgzB +½rvB² p : pression en pascal ; r masse volumique du fluide (eau) kg/m3; z altitude en mètre ; v : vitesse d'écoulement en m/s. Or pA=pB et
zA-zB= 3 et vA=0
d'où : vB² =2
g(zA-zB) = 20*3 = 60 ;
vB= 7,7
m/s. Qv= pr²vB= 3,14*0,022*7,7= 9,7 10-3 m3/s = 9,7 L/s. En supposant le débit constant le temps mis pour vider complétement le réservoir est : volume réservoir (m3) / debit volumique (m3/s) t = 5,3 / 9,7 10-3 =
5,7 102 s.
|
|||
|
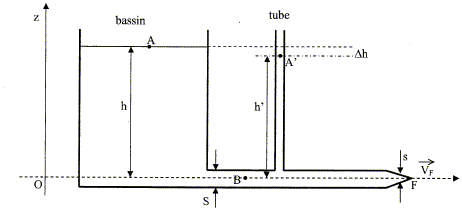
La canalisation fermée à son extrémité présente une fuite en F, on la schématise par un trou de section s. L'eau étant considérée comme un fluide parfait on peut lui appliquer le théorème de Bernoulli ; 1/(2g)( v²2-v²1) +(z2-z1)+(P2-P1)/(rg)=0. La fuite d'eau étant faible, on admet que la hauteur d'eau dans le bassin ne varie pas. Ecrire le théorème de Bernoulli entre les points F (2) et A (1) : d'une part, la surface du récipient étant très grande par rapport à la section du trou, la vitesse de l'eau en A est presque nulle d'autre part, on considère le point F dans le jet d'eau, en contact avec l'air extérieur d'où : PF-PA=0 par suite : 1/(2g)( v²F-0) +(zF-zA)=0 ; 1/(2g) v²F- h=0 soit v²F = 2gh ; vF= (2gh)½. si h = 10 m alors vF= 200½ = 14 m/s. Débit volumique qv de fuite si s = 1 mm² : qv = s vF avec s= 10-6 m² ; qv =10-6 *14 = 1,4 10-5 m3/s. Expression de la valeur de la vitesse V de l'eau dans la canalisation en fonction de vF, S et s : le débit volumique se conserve d'où : s vF = SV ; V= s /S vF =10-6 / 10-4 *14 = 0,14 m/s. Expression de la différence de pression entre les points B et A' en fonction de la hauteur d'eau h' dans le tube : Ecrire le théorème de Bernoulli entre les points B et A : 1/(2g)( V²-v²A) +(zB-zA)+(PB-PA)/(rg)=0 PB-PA =rg[h- V²/(2g) ] L'eau étant en équilibre dans le tube témoin : PB-PA' =rgh' de plus : PA' =PA =pression atmosphérique d'où : rgh' = rgh -½rV² ; h-h'= V²/(2g) Dh = h-h'=V²/(2g) =
0,14²/20 = 10-3 m =
1 mm. Valeur minimale de la section du trou de fuite s, que l'on peut détecter pour S= 1 cm² et h = 10 m : Dh = 5 10-3 m ; V²/(2g) = 5 10-3 soit V² = 0,1 ; V= 0,316 m/s or V= s /S vF soit s = V S/vF = 0,316*10-4 / 14 =2,26 10-6 m² = 2,3 mm². |
|||
|
|