Aurélie 09/11/06
 

CAPES physique chimie ( d'après concours interne 2002 )

Etude de la conduction électrique des métaux

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

 

Résistance d'un fil métallique cylindrique rectiligne homogène de longueur l et de section S :( arguments physiques simples)

La résistance électrique est une mesure de l'opposition que présente un matériau au passage du courant.

Dans un métal, les porteurs de charge sont des électrons libres ; ces derniers se déplacent d'autant plus difficilement qu'ils rencontrent plus d'obstacles ( chocs des électrons libres sur les ions métalliques fixes du réseau cristallin). Les obstacles sont d'autant plus nombreux que le conducteur est plus long et que sa section est plus faible.

Donc R est proportionnelle à l /S = l /(pr²).

On pose la relation R= rl /S, r désignant la résistivité du métal. On réalise une série de mesures de résistance pour de très longs fils cylindriques de fer, de structure homogène, tendus sur des pylônes et de rayons r différents.
r = 5 mm
r=2,2 mm
r=1,5 mm
r=1 mm
l =200 km
250
1285
2770
6250
l = 150 km
185
960
2080
4680
l =100 km
125
640
1390
3120
l = 10 km
12
65
140
310

pour l =200 km :

S=pr2(m²)
7,85 10-5
1,52 10-5
7,0 10-6
3,1 10-6
1/S( m-2)
1,27 104
6,58 104
1,43 105
3,23 105
R (ohm)
250
1285
2770
6250

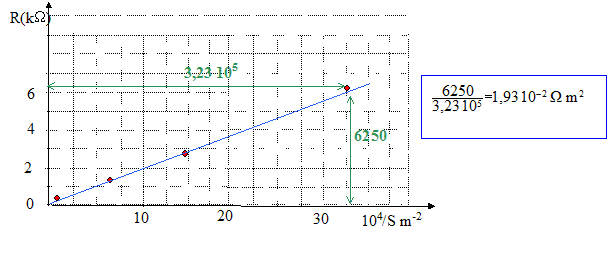
R est proportionnelle à 1/S : le coefficient directeur est égal à rl = 1,93 10-2 W m² soit r = 1,93 10-2 / 200 000 = 9,7 10-8 W m.

pour S =7,85 10-5 m ² :

l (m)
2 105
1,5 105
1 105
1 104
R
250
185
125
12

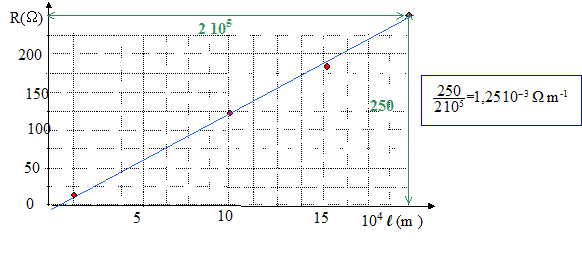
R est proportionnelle à l : le coefficient directeur est égal à r/S = 1,25 10-3 W m-1 soit r = 1,25 10-3 * 7,85 10-5 = 9,8 10-8 W m.

 

On admet que la conduction électrique d'un fil cylindrique peut être décrite de la manière suivante : chaque atome du métal possède un électon libre ; le courant électrique est assimilé au mouvement d'ensemble d'un très grand nombre d'électrons, à une vitesse constante uniforme v.
Soit m la masse volumique du métal et M sa masse molaire exprimée dans le système S.I ( kg /mol).

Expression littérale de la densité volumique d des électrons libres en m-3 :

masse de 1 m3 de fer : m kg ; masse molaire du fer : M kg/mol

quantité de matière de fer dans 1 m3 : m /M mol

nombre d'atome de fer ( donc nombre d'électrons libres) dans 1 m3 : NAm /M

densité volumique de charge : d = NAm /M avec NA : nombre d'Avogadro
Un courant d'intensité I traverse le fil de section droite S. Pendant la durée infinitésimale dt :

Distance dx dont a avancé le flot d'électrons libres à la vitesse v : dx = vdt

Volume dV occupé par les électrons traversant la surface droite S du cylindre pendant cette durée : dV=Sdx =Svdt

Nombre dN d'électrons correspondant : dN=NAm /M dV = NAm Svdt / M

Valeur absolue de la charge |dq| totale :|dq|=NAm e Svdt / M avec e : charge élémentaire ;

Valeur absolue de l'intensité |I|= |dq|/dt = NAm e Sv / M
Relation entre I, e, d, S et v : |I|= Sved
Calcul dans le cas du fer la valeur de d : m = 7,86 103 kg m-3 ; M= 55,8 10-3 kg/mol

d = NAm /M = 6,02 1023*7,86 103 / 55,8 10-3 = 8,48 1028 m-3.

Calcul de v si I/S= 10 A mm-2 = 107 A m-2 : v = |I|/(Sed) = 107/ ( 1,6 10-19 *8,48 1028 )=7,4 10-4 m/s = 0,74 mm/s.

Cette vitesse moyenne de déplacement d'ensemble des électrons libres est très faible. ( en particulier par rapport des vitesse de ces mêmes électrons animés de mouvements désordonés , en absence de champ électrique).


retour -menu