Aurélie 11/04/07
 

Concours Capes : Résolution d'une équation différentielle à l'aide des nombres complexes 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

 

Les vecteurs sont écrits en gras et en bleu.

Le rotor du moteur asynchrone est une bobine plate, fermée sur elle même, de surface totale S=Suz, de résistance R, d'inductance L qui peut tourner autour de l'axe (Oz) passant par son centre et perpendiculaire à S. La bobine est solidaire d'un volant de grand moment d'inertie régularisant sa vitesse de rotation WS =wSuz. Le rotor du moteur asynchrone ressent le champ magnétique crée par le stator, de valeur constante B0, tournant autour de l'axe (Oz) à la vitesse angulaire constante WB =wBuz. Le retard de phase initial de la bobine sur le champ tournant est j.

Equation différentielle qui régit le courant i(t) dans la bobine du rotor en fonction de R, L et de Fext, le flux du champ magnétique extérieur à travers la bobine du rotor.

 

Dans le plan (Oxy), représentation du champ tournant B et du vecteur surface S :

 

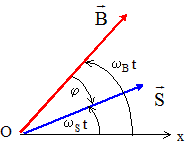
Expression de Fext en fonction de t, B0, S, wB, wS et j.

Fext(t) = B(t) . S(t) avec Bx(t) = -B0sin( wB t ) ; By(t) =B0 cos( wB t )

et Sx(t) = S sin( wS t -j) ; Sy(t) =B0 cos( wS t -j )

Fext(t) = Bx(t)Sx(t) + By(t)Sy(t)

Fext(t) =B0S [-sin( wB t )sin( wS t -j) +cos( wB t )cos( wS t -j )]

Or -sin( wB t )sin( wS t -j) +cos( wB t )cos( wS t -j ) = cos (( wB-wS)t +j)

Fext(t) =B0Scos (( wB-wS)t +j).
 

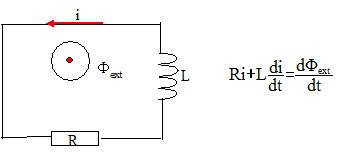
Expression de Imax en fonction de w, R, L, B0 et S :

L''équation différentielle est résolue par la méthode des nombres complexes ; on pose w = wB-wS

Ri + Ldi/dt =d Fext/dt ; Fex = B0Scos( wt +j) ; i(t) = Imax cos(wt+j-Y).

grandeur physique
i(t)
di/dt
d Fext/dt
nombre complexe associé
Imax exp j(j-Y)
jwImax exp j(j-Y)
jw B0Sexp jj
L'équation différentielle s'écrit alors :

R I max exp j(j-Y) + jLwImaxexp j(j-Y)= jw B0Sexp jj.

(R+jLw)I maxexp j(-Y) = jw B0S

Par suite en égalant les modules [R2+(Lw)2 ] I2 max = (w B0S)2.

Imax= w B0S [R2+(Lw)2 ] -½.

arg [(R+jLw)I max] -Y = arg ( jw B0S)

Y = arg ( jw B0S) - arg [(R+jLw)I max]

arg ( jw B0S) = ½p ; arg [(R+jLw)I max] = tan-1(Lw/R).

Y =½p -arctan(Lw/R).

½p -Y =arctan(Lw/R) ou sin(½p -Y )= cosY =Lw /[R2+(Lw)2 ] -½ .

 
 

retour -menu