|
|
|
|
|
|
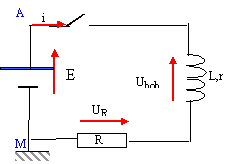
On se propose d'étudier l'établissement du courant au travers d'une bobine inductive et résistive lorsque celle-ci est soumise à un échelon de tension. Pour obtenir une indication sur la durée nécessaire à l'établissement d'un régime permanent, on utilise la grandeur notée t, appelée constante de temps du circuit et définie par t = L / S
 |
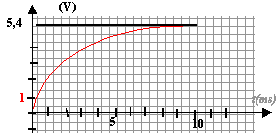 |
- Soit I l'intensité du courant électrique qui traverse le circuit, en régime permanent. Etablir son expression littérale à partir des caractéristiques du circuit. Déterminer sa valeur numérique.
- Pendant le régime transitoire, on admet que
l'intensité du courant atteint 63 % de sa valeur
maximale I au bout d'un temps t.
- Montrer que l'expression de t est homogène à un temps.
- Déterminer la valeur de t, constante de temps du circuit, à partir du graphique
- En déduire une valeur approchée de L.
B. Vérification de l'expression littérale de t : Pour effectuer cette détermination, l'expérience réalisée dans la partie A est reprise en conservant pour R la valeur de 50 W, mais en donnant à L différentes valeurs, 0,20 H puis 0,40 H puis 0,60 H et enfin 0,80 H. Les enregistrements effectués permettent d'obtenir le faisceau de courbes ci-dessous :
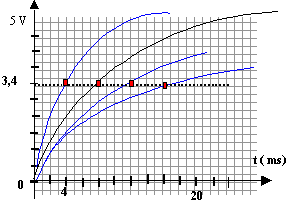
- Déterminer, à partir des
enregistrements effectués, les valeurs de
t correspondant aux
différentes valeurs de L et compléter le
tableau ci-dessous. Ce tableau est à reproduire
sur votre copie.
L en H 0,2 0,4 0,6 0,8 t en ms - A partir des résultats de cette étude expérimentale, trouver la relation existant entre t et L.
- En déduire la valeur expérimentale de R. Est-elle en accord avec les données ?
C. On admet que pour l'établissement du courant dans ce circuit, l'intensité est donnée par une relation du type i = A.e-t/t + B .
- Déterminer en expliquant votre démarche, les expression de A et B.
- En déduire la relation littérale complète donnant i.
- Exprimer cette relation avec les valeurs numériques de la partie A.
.
corrigé
uR + ubob = E ; uR = Ri ; ubob = ri+Ldi/dt ; en régime permanent di/dt =0
I= E/(R+r) = 5,4 / 50 = 0,108 A.
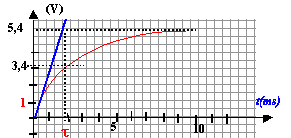
tracer la tangente à la courbe à la date t=0 ; cette tangente coupe l'asymptote horizontale à la date t = 2 ms= 2 10-3 s.
t = L / (R+r) soit L= (R+r) t = 50*2 10-3 = 0,1 H.
ubob = Ldi/dt soit L = ubob dt/di
L est en volt* seconde / ampère : V s A-1 ; R est en volt / ampère : V A-1 ;
t s'exprime en : V s A-1 V-1 A soit en seconde.
|
|
|
|
|
|
|
|
|
|
|
|
tracer une droite horizontale à u = 5,4*0,63 = 3,4 V ; elle coupe les courbes à des dates égales aux différentes constantes de temps.
i = A.e-t/t + B
au bout d'un temps suffisamment long, le régime permanent est atteint et le terme e-t/t s'annule : l'intensité est égale à B soit 0,108 A.
à t = 0, fermeture de K, l'intensité est nulle : 0 = A+B soit A= -B
i = B(1-e-t/t ) avec t = L / R = 2 ms
i = 0,108 (1-e-t/2 ) avec t en ms et i en ampère.
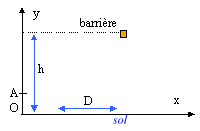
Un jeu d'enfant, schématisé partiellement ci-dessous, est constitué d'une piste sur laquelle une petite voiture peut se déplacer, guidée électriquement à l'aide d'une manette. On peut ainsi lui communiquer la vitesse désirée, ou lui faire effectuer diverses actions. L'une d'elles, consiste à éjecter une bille, de masse m, à l'aide d'une catapulte verticale placée dans ce véhicule. La bille doit ainsi passer au-dessus d'une barrière placée au-dessus du circuit, la difficulté consistant à provoquer l'éjection de la bille au bon moment pour y parvenir. Les dimensions sont les suivantes: h = 20 cm, m = 20,0 g , d0 = 5,0 cm. On supposera que lorsque la bille quitte le ressort, elle possède une vitesse verticale v0 = 2,0 m.s-l et se trouve à une hauteur d0 au-dessus du sol. On prendra g = 10 m/s². Dans tout l'exercice, l'action de l'air sera négligée. Le point de départ de la bille A sera pris comme origine du mouvement. L'origine du repère 0 est sur le sol à la verticale de A.
- La voiture roulant sur une portion rectiligne, horizontale et à la vitesse constante v, telle que vi = 1,0 m.s-1, établir dans le repère (Ox, Oy) indiqué, les équations horaires paramétriques de cette bille.
- En déduire l'équation cartésienne de sa trajectoire. L'exprimer d'abord de façon littérale, puis avec les données numériques fournies.
- Afin de réussir à faire passer la bille au-dessus de l'obstacle à franchir, déterminer entre quelles valeurs de D il faudra provoquer l'éjection de la bille.
- Déterminer l'abscisse de cette bille lorsqu'elle repassera dans le plan horizontal passant par A. ( Portée de ce tir)
- Quel temps aura-t-elle mis pour la parcourir ?
- Pendant ce temps-là, quelle sera la distance effectuée par la voiture qui a continué sa course à la même vitesse ?
- Pouvez-vous en déduire où devrait
retomber la bille si le tir est réussi.
corrigé
avant éjection, la bille a un mouvement rectiligne uniforme x = vit = t et y = d0 = 0,05 m.
après éjection, la bille est en chute libre :
les vecteurs sont écrits en bleu et en gras.
a(0 ; -g); vinit ( vi ; v0) ; OM0(0 ; d0)
la vitesse est une primitive de l'accélération v(t) [vi ; -gt+v0]
le vecteur position est une primitive de la vitesse OM(t) [x = vi t ; y = -½gt²+v0 t ; v0t + d0]
trajectoire : t = x / vi ; report dans y : y = -½gx² / v²i + v0 x / vi + d0.
y = -5x² +2x + 0,05.
la bille passe au dessus de la barre si y >0,2 :
-5x² +2x+0,05 >0,2 ; x² - 0,4 x +0,03 < 0
D = 0,04 ; x1 = 0,1 ; x2 = 0,3 et 0,1< D < 0,3 m.
portée : y = 0,05 ; -5x² +2x = 0 donne x1=0 et x2 = 0,4 m.
durée : x = vi t donne t = 0,4 / 1 = 0,4 s.
distance parcourue par la voiture : 0,4 m ; la bille retombe sur la voiture.
On se propose d'identifier le couple acide/base noté HA/A- parmi les couples ci-dessous
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- Une solution S1, contenant l'espèce A-, de concentration molaire C1 = 0,10 mol/L
- Une solution S2, contenant l'espèce
HA, de concentration molaire C2 = 0,mol/L
- Avec un pH-mètre, on mesure le pH de plusieurs
mélanges réalisés dans des
béchers. Les résultats sont regroupés
dans le tableau ci-dessous où V1
représente le volume de solution S1, et
V2 le volume de solution S2
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- Tracer la courbe pH = f (log (V1 / V2)
- On admet que log (V1 / V2) = log([A-]éq /[AH]éq). Déduire de la courbe la relation qui existe entre pH et log([A-]éq /[AH]éq).
- Ecrire l'équation de la réaction entre l'acide HA et l'eau. En déduire la constante d'acidité Ka du couple HA/A-, puis la relation liant le pH de la solution et le pKa du couple HA/A-.
- Déduire des questions précédentes une valeur approchée du pKa du couple.
B. Identification du couples acide/base HA/A-:
- Quels sont les couples acide/base du tableau que l'on peut éliminer à l'issue de l'étude de la question A ?
- On a dû peser 1,85 g d'acide HA pour
réaliser 250 mL de solution S2 de
concentration C2 = O, 1 mol/L
- Déterminer la masse molaire du composé HA.
- Identifier le couple HA/A-.
corrigé
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
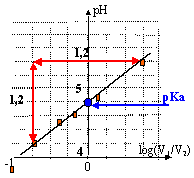
le coefficient directeur de la droite est voisin de +1 (fonction est croissante)
ordonnée à l'origine : 4,8
fonction affine : pH = log(V1/V2) + 4,8 = log ( [A-] / [AH]) + 4,8
AH + H2O = A- + H3O+
Ka=[A-][H3O+]/[AH ]
log Ka = log( [A-] / [AH]) + log [H3O+]
- log [H3O+] = log( [A-] / [AH]) - log Ka
pH = log( [A-] / [AH]) + pKa donc pKa proche de 4,8.
parmi les couples donnés on élimine ceux dont le pka est trop différent de 4,8 soit :
HCOOH / HCOO- et HClO / ClO-
Quantité de matière (mol) d'acide = volume (L) * concentration (mol/L)
n = 0,25*0,1 = 0,025 mol
Quantité de matière (mol) d'acide = masse (g) / masse molaire (g/mol)
masse molaire (g/mol) = 1,87 / 0,025 = 74,8 g/mol environ 74 g/mol
donc on retient le couple H5C2-COOH / H5C2-COO-
acide propanoïque / ion propanoate