|
d'après technicien labo 03 |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
électronique: étude d'un multiplieur électronique :
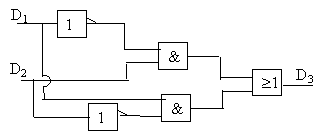
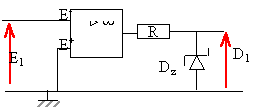
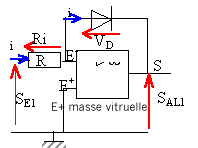
la tension de sortie us ne peut prendre que deux valeurs + usat ou - usat . de plus D1 = tension aux bornes de la diode zener. si E1 positif; alors la tension de sortie us vaut + usat : tension aux bornes de la diode zener : D1 =0. si
E1 négatif; alors la tension de sortie
us vaut - usat : tension aux bornes de
la diode zener : D1 =
Dz.
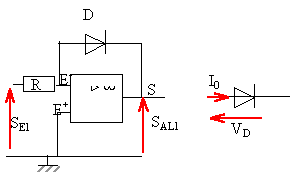
SE1=Ri ; SAL1 = -VD. SE1=Ri0 exp (VD / Vm) =Ri0 exp (-SAL1 / Vm) ln(SE1/(Ri0 ) = -SAL1 / Vm SAL1
= - Vmln(SE1/(Ri0
)
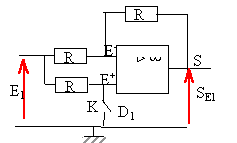
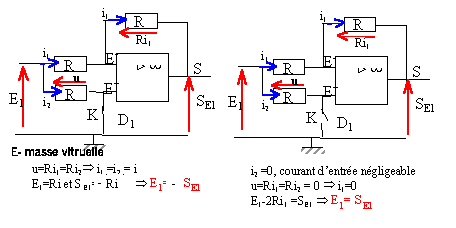
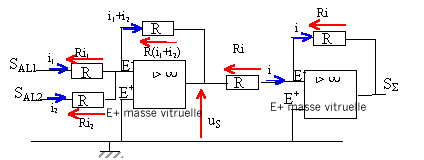
SAL1 = Ri1 ; SAL2 = Ri2 ; uS = - R(i1+i2) = -(SAL1 +SAL2 ) SS = -Ri ; uS = Ri soit SS = -uS ; SS
= SAL1 +SAL2
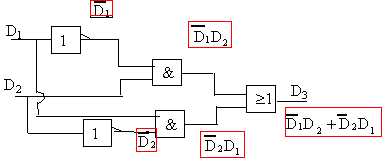
fonction ou
exclusif
|
||||||||||||||||||||||||||||||||||||
|
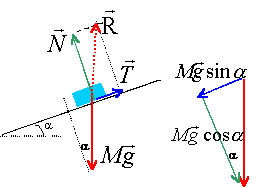
plan incliné : les grandeurs écrites en gras et en bleues sont des vecteurs. A l'instant t=0, un pavé (S), de masse m= 1kg est posé sans vitesse initiale sur un plan incliné d'un angle a par rapport à l'horizontale, fixe dans le référentiel terrestre supposé galiléen. (S) est susceptible de glisser sur le plan incliné; on envisage pas l'éventualité d'un basculement. On prendra g= 9,8 m/s². Le plan
incliné exerce sur S une force R
qui s'exprime sous la forme R=
Rt ex
+ Rn ey.
Suivant que (S) glisse ou ne glisse pas sur le plan
incliné, les composantes tangentielle Rt
et normale Rn de la force de contact
R
vérifient des conditions différentes : 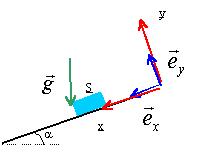
corrigé On not RN par N et RT par T. f est sans dimension car f = |T|/|N|, rapport de deux forces. principe fondamental de la dynamique : P + N+T = ma projection sur l'axe des y : Mg cos a - N=0 N =Mg cos a ; la composante normale est positive. le solide se met en mouvement dès que Mg sin a supérieur ou égal à T cas limite : |T|= Mgsin a et f = |T|/|N| = tan a. a = tan -10,2 = 11,3°. la composante tangentielle est négative.
travail de R : la composante N, perpendiculaire à la vitesse ne travaille pas. la composante T, colinéaire à la vitesse effectue un travail résistant : W R = - T d avec |T |= f N = f Mg cos a = 0,2*1*9,8*cos20 = 1,84 N W R = - 1,84*0,75 = -1,381 J. énergie cinétique finale : Ec=½Mv² = 0,5*1*1,5² = 1,125 J. l'énegie cinétique initiale étant nulle, la variation d'énergie cinétique vaut : 1,125 J. WPoids +W R = 1,133 J très proche de DEc. On retrouve l'expression du théorème de l'énergie cinétique.
|
||||||||||||||||||||||||||||||||||||
|
Un laser, de longueur d'onde l, éclaire un réseau de pas a sous incidence normale. On observe sur un écran de grande taille, placé à une distance d = 30 cm derrière le réseau un certain nombre de taches lumineuses dans des directions qk ( k=....,-2, -1, 0, 1, 2, .... : cf figure). A chaque valeur de l'entier k correspond "un ordre".
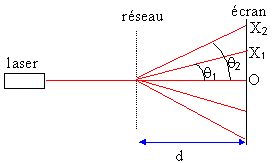
Les taches lumineuses sont également repérées par leur abscisses Xk par rapport au centre O de l'écran (O est le point d'impact du laser en l'abscence de réseau).
Toutes les vibrations diffractées dans la direction qk, par toutes les fentes du réseau vont interférer. les interférences sont constructives (maximum d'intensité lumineuse) si la différence de marche est proportionnelle à un nombre entier de longueur d'onde : d = k l. la différence de marche est égale à : a sinqk . a sinqk =k l soit sinqk =k l / a. k entier nul, positif ou négatif. l : longueur d'onde de la lumière laser (m) a: pas du réseau (m), distance séparant deux traits consécutifs. n = 1/ a : nombre de traits par unité de longueur ;500 traits par mm n = 500*1000 = 5 105 traits par mètre ; a = 1/ 5 105 = 2 10-6 m. si k = 1 alors tan q1 = X1 / d = 0,1 / 0,3 = 0,333 soit q1 =18,4° sin q1 =0,316 et l = 2 10-6 *0,316 = 0,632 10-6 m = 0,632 m m = 632 nm.
taille minimale de l'écran (hauteur) = 2*0,891 = 1,78 m.
|
||||||||||||||||||||||||||||||||||||
|
synthèse d'alcène : La déshydratation du 2-méthylbutan-2-ol (CH3)2COH-CH2-CH3 donne en milieu acide deux alcènes. L'alcène le plus substitué est noté A1 et le moins substitué est noté A2.
corrigé (CH3)2C=CH(CH3) 2-méthylbut-2-éne (A1) H2 C=C(CH3) C2H5 2-méthylbut-1-éne (A2) densité de la solution commerciale d = 1,71 soit : la masse de 1L vaut 1710 g et contient 85 % en masse d'acide orthophosphorique soit : 1710*0,85 =1453,5 g masse molaire de cet acide :98 g/mol Quantité de matière de cet acide dans 1L (concentration) : 1453,5 / 98 =14,83 mol/L facteur de dilution : 14,83 / 8 =1,853. volume de
solution commerciale à prélever : 100 / 1,853
= 54
mL.
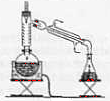
Introduire 25 mL de 2-méthylbutan-2-ol dans le ballon à l'aide d'une pipette jaugée de 25 mL(+ pipeteur) prélever 10 mL d'acide orthophosphorique à 8 mol/L à l'aide d'une pipette jaugée de 10 mL ; placer dans une ampoule de coulée fixée sur le ballon puis ouvrir doucement le robinet de l'ampoule. la pierre
ponce régularise l'ébullition : elle peut
être remplacée par de petites billes de verre.
l'acide phosphorique a une structure tétraèdrique: le phosphore occupe le centre du tétraèdre; les goupes OH et l'atome d'oxygène occupe les 4 sommets..
ballon surmonté d'une colonne de Vigreux elle même surmontée d'un thermomètre ; réfrigérant à eau incliné avec arrivée de l'eau à la partie la plus basse. le distillat est recueilli dans un erlenmeyer chauffe
ballon électrique.
peser 5 g de carbonate de sodium à la balance de précision; dissoudre dans un bêcher avec de l'eau distillée ; placer dans une fiole jaugée de 100 mL et compléter avec de l'eau distillée jusqu'au trait de jauge. L'ion carbonate CO3 2- est une base et réagit avec l'acide orthophosphorique ( réaction acide base) : il se dégage du dioxyde de carbone. Il faut penser à retour - menuner l'ampoule à décanter, puis ouvrir le robinet afin de supprimer la surpression due au dégagement de CO2. CO3
2- + 2H3PO4 -->
CO2 +2 H2PO4- +
H2O
Le sulfate de magnésium anhydre est un déshydratant, il élimine toute trace d'eau. L'alcène
A1 distille à 38°C ; l'alcène
A2 distille à 31°C.
d'alcool (réactif de départ) : 1 mL a une masse de 0,81 g. 25*0,81 = 20,25 g ou 20,25 / 88,15 = 0,230 mol d'alcène A1 : 11,8 g ou 11,8 / 70,14 = 0,168 mol rendement 0,168/ 0,23 =0,73 (73 %) La fonction alcène est susceptible de décolorer l'eau de brome ou une solution de permanganate de potassium.
|
||||||||||||||||||||||||||||||||||||
|
Dosage de l'éthanol contenu dans une boisson : La méthode de dosage comporte deux étapes : - On oxyde l'éthanol en milieu acide sulfurique par un excès de dichromate de potassium. - on réduit l'ecxès de dichromate en milieu acide par une solution titrée de sulfate de fer (II).
Données : densité de l'alcool par rapport à l'eau d= 0,8 ;masse molaire éthanol : 46,07 g/mol corrigé 2 fois {Cr2O72-+ 14H+ + 6e- = 2Cr3++ 7H2O} réduction 3 fois { CH3CH2OH +H2O = CH3COOH + 4e- + 4H+} oxydation 2Cr2O72-+ 3CH3CH2OH + 16H+ --> 4Cr3++ 3CH3COOH +11H2O Cr2O72-+ 14H+ + 6e- = 2Cr3++ 7H2O réduction 6 fois { Fe2+ =Fe3+ + e-} oxydation Cr2O72-+
14H+ + 6Fe2+ -->2Cr3++
7H2O +6Fe3+
3,4 10-4 = 10-3 -2/3n d'où n = 0,66 10-3 *3/2 = =9,9 10-4 mol dans 10 mL de S soit 9,9 10-3 mol d'alcool dans S soit en masse : 9,9 10-3 * 46,07 = 0,456 g et en volume : 1 mL a une masse de 0,8 g 0,456/0,8 = 0,57 mL Or il faut tenir compte de la dilution de la boisson ( facteur de dilution = 10) : donc 5,7 mL d'alcool pur dans la fiole jaugée de 100mL soit 5,7 % en volume 9,9 10-3 mol d'alcool dans la fiole jaugée de 100 mL [éthanol] fiole jaugée =9,9 10-3 / 0,1 =9,9 10-2 mol/L [éthanol] boisson =9,9 10-2 *10 =9,9 10-1 mol/L. |