d'après concours kiné Strasbourg 03 physique 1 h - chimie ½ h- sans calculatrice.

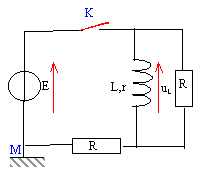
dipôles Soit le circuit suivant : L'interrupteur K est fermé. A un instant considéré comme initial on ouvre l'interrupteur K. L= 10 mH ; R= 100 W ; E= 10 V, r =10 W. A- Avant l'ouverture de l'interrupteur, l'intensité du courant délivré par le générateur vaut 50 mA. B- Après ouverture de K la tension aux bornes de la bobine devient négative. C- Après ouverture de K la tension aux bornes de la bobine tend vers zéro. D- Après ouverture de K, l'énergie emmagasinée dans la bobine devient négative. K fermé : en régime permanent i = E / résistance du dipôle résistance équivalente à r et R en parallèle : R1 = rR/(r+R) = 10*100 / (10+100) = 9,09 W. résistance équivalente à r et R1 en série : R1+R = 109,09 W. intensité i = 10/109,1 = 91,6 mA. uL = R1i = 9,1*0,0916 = 0,83 V K ouvert : uL décroît de 0,83 V jusqu' à zéro. C vrai l'énergie stockée (½Li² =0,5 *0,01 *0,0916²=4,2 10-5 J) est perdue sous forme de chaleur dans les résistances r et R. Cette énergie tend vers zéro.   Soit un dispositif réalissant des oscillations électriques à l'aide d'uncircuit RLC. On observe la tension aux bornes du condensateur. On donne t2 = 10 ms. 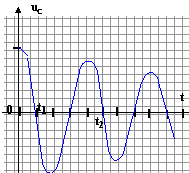A- La tension aux bornes du dipôle ohmique est nulle en t1. B- Le régime observé est pseudo-périodique et la pseudo-période vaut 10 ms. C- On peut considérer que la pseudo-période vaut environ la période propre du circuit LC non amorti. D- L'énergie stockée par le condensateur à t2 est nulle. à t1, la tension uC est nulle : la bobine stocke toute l'énergie du dipôle et l'intensité est alors maximale. La tension aux bornes de R n'est pas nulle uR= Ri La pseudo-période vaut environ 8 ms. si l'amortissement est faible , la période propre du circuit LC est voisine de la pseudo-période. à t1, la tension uC est nulle : le condensateur ne stocke pas d'énergie C et D vrais On réalise le circuit suivant : On ferme l'interrupteur. On observe alors la tension uC aux bornes du condensateur. La solution de l'équation différentielle vérifiée par uC s'écrit : uC= E(1-exp(-t / (3RC)) ; uC= E(1-exp(-t / (2RC)) ; uC= E exp(-t / (2RC)-1) ; uC=E exp(-t / (3RC)-1) ; K fermé : C est en série avec une résistance égale à 2R ; t = 2RC uC= E(1-exp(-t / (2RC))

ondes Dans un milieu dispersif la célérité d'une onde progressive périodique mécanique dépend : A- Uniquement du milieu. B- De la fréquence de l'onde. C- De la période de l'onde. D- de l'amplitude de l'onde du milieu et de la fréquence ( donc de la période) B et C vrais On provoque simultanément à l'instant t=0 deux perturbations transversales de même forme et de même sens aux deux extrémités d'une corde tendue de longueur 10 m. La célérité des ondes le long de cette corde est de 20 m/s. A l'instant t=0, l'amplitude de la perturbation est nulle aux extrémités de la corde. 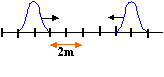A- La corde est représentée à la date t= 0,10 s. B- Les fronts des deux ondes se rencontrent à l'instant t= 0,2 s. C- La durée de chaque perturbation est de 0,1 s. D- A l'instant t= 0,3 s on observe une perturbation transversale unique. distance parcourue par la perturbation à t = 0,1 s : d = 20*0,1 = 2 m alors que le dessin indique 3 m. à t = 0,3 s , les deux perturbation se recouvrent exactement ( addition) C et D vrais   Une onde sonore de fréquence 400 Hz se propage dans une tige métallique avec une célérité de 3000 m/s. A- L'onde se propage transversalement B- Deux points distants de 15 m sont en phase. C- Deux points distants de 26,25 m sont en opposition de phase. D-Deux points distants de 35 m sont en opposition de phase. deux points en phase sont distants de k l ( k entier) ; l = 3000 / 400 = 7,5 m deux points en opposition de phase sont distants de (2k+1) ½l ( k entier) ; 26,25 / (0,5*7,5) = 7 ; 35 / (0,5*7,5) =9,3 7 est un entier impair ; 9,33 n'est pas un nombre entier B et C vrais On observe à l'aide d'un faisceau laser, de longueur d'onde dans le vide l0 = 600 nm une fente de largeur a = 0,1 mm et de centre O découpée dans un écran E'. On place à la distance D= 2 m et parallèlement à E' un écran E. On observe sur cet écran une tache centrale brillante de centre A, et des taches latérales brillantes, symétriques par rapport à A et de moins en moins lumineuses à mesure que l'on s'éloigne de A. Soient B et B' les centres des taches sombres qui encadrent la tache centrale. A- Le phénomène observé est celui de la réfraction de la lumière. B- L'angle q= angle (AOB), appelé écart angulaire vaut 0,012 rad. C- La largeur de la tache centrale vaut 2,4 cm. D- la position des taches sombres dépend de la longueur d'onde. 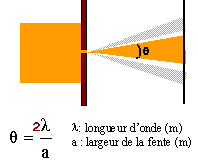phénomène de diffraction angle (AOB) = ½q = l /a = 600 10-9 / 10-4 = 6 10-3 rad ; tan q = ½largeur tache centrale / D soit largeur = 2 D tanq = 2*2*6 10-3 =2,4 10-2 m = 2,4 cm. 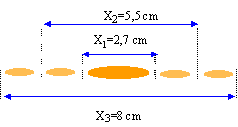C vrai X2 = 2 X1 et X1 = 2lD/a D vrai L'énergie d'ionisation d'un atome d'hydrogène pris dans son état fondamental est de 13,6 eV. A- Il est impossible d'ioniser un atome d'hydrogène en le bombardant avec des électrons de vitesse égale à 1,8 106 m/s B- Si on se place dans l'hypothèse où l'atome est ionisé, alors l'énergie de l'électron émis est quantifiée. C- La longueur d'onde de la radiation susceptible d'ioniser l'atome d'hydrogène à partir de son état fondamental est approximativement de 10-7 m D- Un électron d'énergie cinétique 2 eV vient heurter un atome d'hydrogène au niveau correspondant à n=3, d'énergie E3= -1,5 eV: l'atome s'ionise. h= 6,63 10-34 J s ; e = 1,6 10-19 C ; c= 3 108 m/s ; masse électron : 9,1 10-31 kg ; 1,8² voisin 3,2. ½mv² = 0,5*9,1 10-31*(1,8 106)² = 4,05*3,64 10-18 = 14,8 10-19J 14,8 10-19 / 1,6 10-19 = 9,2 eV, insuffisant pour ioniser l'atome car inférieur à 13,6 eV. E = 13,6 * 1,6 10-19 = 2,2 10-18 J ; l = hc/E = 6,6 10-34*3 108 / 2,2 10-18 = 9 10-8 m C et D vrais

mécanique   Un oscillateur est constitué par une masse ponctuelle m = 0,2 kg accrochée à un ressort de raideur k = 5 N/m. La masse oscille sans frottement suivant un axe (x'Ox) horizontal sur lequel on la repère par son abscisse x. Lorsque le ressort est non allongé, x=0. A l'instant t=0 la masse est située à l'origine et est animée d'une vitesse de 60 cm/s vers les x négatifs. L'équation horaire du mouvement est donnée dans le système S.I par : A- x= -0,12 sin(5t) B- x= 0,6 sin( 0,2t) C- x= 0,12 sin(5t) D- x= - 0,6 sin(5t + ½p) w² = k/m= 5 / 0,2 =25 et w = 5 rad/s. à t = 0 , x=0 donc fonction sinus conservation de l'énergie mécanique du système {mase- ressort} : ½ka² = ½mv²max. a² = m/kv²max = 0,2 / 5 *0,6² = 144 10-4 soit a = 0,12 m le solide se dirige vers les x négatifs à t =0 A vrai On enregistre l'amplitude oscillatoire d'un dispositif constitué par un ressort de raideur k à l'extrémité duquel est fixé un solide de masse M. L'ensemble est soumis à un dispositif d'amortissement équivalent à une force de frottement fluide. Un oscillateur mécanique impose une fréquence oscillatoire au système masse ressort. On relève l'amplitude oscillatoire en fonction de la fréquence imposée par l'excitateur pour deux amortissements différents, l'un faible, l'autre plus fort. k= 1,8 N/m et M= 0,5 kg. 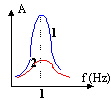A- La courbe 1 correspond à l'amortissement le plus faible. B- La pulsation du système ressort-masse vaut environ 6 rad/s. C- Les deux courbes caractérisent un phénomène de résonance. D- Seule la courbe 2 caractérise un phénomène de résonance. fréquence de résonance f = 1 Hz ; w = 2p f = 6,28 rad/s. courbe 2 : faible amplitude, amortissement grand, donc résonance "floue", peu marquée. A et B vrais Une bille d'acier de rayon r = 5 mm tombe verticalement dans l'eau. La valeur de la force de frottement fluide exercée par l'eau a pour expression F= KAreauV² où A = pr² est la surface de la section droite de la bille et K un coefficient constant qui dépend de la forme du solide. On néglige la poussée d'Archimède. reau= 1000 kg/m3 ; racier = 8000 kg/m3 ; K= 0,2 ; g = 10 m/s² ; racine carrée (8/3)=1,6 ; racine carrée (20/3)= 2,6. A- L'équation différentielle du mouvement du centre d'inertie G de la bille est : mdv/dt + KAreauV² = mg. B- L'équation différentielle du mouvement du centre d'inertie G de la bille est : mdv/dt - KAreauV² = mg. C- La valeur de la vitesse limite est 2,6 m/s. D- La valeur de la vitesse limite est 1,6 m/s. poids, vertical vers le bas , valeur mg ; frottement, vertical vers le haut, valeur : KAreauV² la seconde loi de Newton s'écrit, en projection sur un axe vertical vers le bas : mg-KAreauV² = ma = mdv/dt mdv/dt + KAreauV² = mg vitesse limite v²lim = mg / (KAreau) volume de la bille : 4/3 p r3 ; masse de la bille : 4/3 p r3 racier ; K= p r² v²lim =4rg racier / (3Kreau) = 4*5 10-3 *10*8000/(0,2*3*1000)= 8/3 ; vlim = 1,6 m/s. A et D vrais Un satellite de masse m, considéré comme ponctuel, est mis en orbite circulaire autour du centre de la terre. Il évolue à une altitude z par rapport à la surface de la terre. La terre est de rayon R et de masse M. A- Le satellite subit une force d'attraction de valeur : F=GM/(R+z)² B- L'accélération du satellite est centrifuge. C- La période de révolution du satellite est T= 2p(R+z)3/2 / (GM)½. F= MGm / (R+z)² ; a = GM/(R+z)² = v²/(R+z)centripète v² = GM/(R+z); période T : durée pour décrire une circonférence de rayon R+z à la vitesse v 2p(R+z) = vT soit 4p²(R+z)² = v²T² = GM T²/(R+z); T² = 4p²(R+z)3 / (GM). C vrai On considère le mouvement du centre d'inertie G d'un solide en chute libre lancé verticalement à partir du sol, dans un champ de pesanteur uniforme avec une vitesse v0 non nulle.  A- La trajectoire de G est toujours une parabole. B- Au sommet de la trajectoire , vG est nulle. C- La valeur vG de la vitesse de G dépend de l'altitude du projectile et de sa vitesse initiale. D- L'altitude du sommet ne dépend que de la valeur v0 de la vitesse initiale. lancé vertical : trajectoire rectiligne au sommet de la trajectoire verticale, la vitesse est nulle conservation de l'énergie mécanique du solide : au départ : ½mv²; au sommet : mgh ; v² = 2gh h : différence d'altitude entre le départ et le sommet ; h dépend de la vitesse initiale et de g. B et C vrais A l'intérieur d'un aérostat, l'air contenu dans une enveloppe est remplacé par du dihydrogène. On suppose que la masse de l'enveloppe est de m = 88 kg. La masse de la nacelle est notée M. l'enveloppe contenant le gaz a un volume V= 400 m3. L'air environnant a une masse volumique rair = 1,2 kg/m3 et H2 a une masse volumique rH2 = 0,08 kg/m3. g = 10 m/s². A- La valeur de la poussée d'Archimède est de 4800 N. B- La valeur de la poussée d'Archimède est de 320 N. C- La valeur maximale de M pour que l'aréostat décolle est de 392 kg. D- La valeur maximale de M pour que l'aréostat décolle est de 360 kg. poussée d'Archimède due à l'air extérieur : Vrair = 400*1,2*10 = 4800 N poids de la nacelle, de l'enveloppe et du dihydrogène ( enveloppe fermée) : g(M+88 + 0,08*400 )= (120+M)g si 4800 >(120+M)g alors on décolle ; M<360 kg A et D vrais On a représenté la vitesse v en fonction du temps pour un mobile se déplaçant sur un plan horizontal. 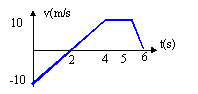A- Le mouvement du mobile est uniforme durant les 4 premières secondes. B- la valeur de l'accélération du centre d'inertie du mobile à t = 5s = est de 10 m/s². C- Le mouvement du mobile ne peut qu' être rectiligne durant les 4 premières secondes. D- Le mouvement du mobile change de sens à t = 5s. 0<=t<2s : la valeur de la vitesse décroît de 10 à 0 m/s a = (0-10)/2 = -5 m/s² à t = 2s, arrêt puis changement de sens. 2<t<=4s , la valeur de la vitesse croît de 0 à 10 m/s ; a = 10/2 = 10 m/s² 4<t<=5, la valeur de la vitesse est constante, mouvement uniforme. 5<t<=6, la valeur de la vitesse décroît de 10 à 0 ; a = -10 m/s². C vrai   Un skieur de masse m=90 kg s'élance à partir d'une position de repos sur une piste rectiligne, inclinée d'un angle a = 30° par rapport à l'horizontale. La valeur F des forces de frottements varie avec la vitesse selon la loi F= kv² avec k=0,5. A- k est en kg m-1. B- L'équation différentielle du mouvement du centre d'inertie de G du skieur est : mg sin 30 - kv² = m dv/dt. C- L'équation différentielle du mouvement du centre d'inertie de G du skieur est : mg cos 30 - kv² = m dv/dt. D- La vitesse limite que peut atteindre le skieur au bout d'un temps très long est 30 m/s. F=kv² soit k = F/v²; force = masse * accélération : kg m s-2 ; vitesse ² : m² s-2. k : kg m s-2 m-2 s² soit kg m-1. poids du skieur, vertical vers le bas, valeur mg frottement parallèle au plan, sens contraire à la vitesse, valeur F=kv² action normale du plan, perpendiculaire au plan, valeur N=mg cos30 la seconde loi de Newton s'écrit sur un axe parallèle au plan dirigé vers le bas : mg sin 30 -kv² = ma = mdv/dt vitesse limite v²lim =mg sin 30 /k = 90*10*0,5 / 0,5 = 900 ; vlim = 30 m/s. A, B et D vrais

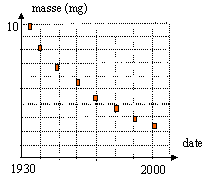
radioactivité   Un laboratoire étudie un échantillon de césium 137 de date de fabrication et de masse inconnues. Le graphe représente l'évolution de la masse de césium 137 en fonction du temps. La demi-vie du césium 137 est : 1957 ans ; 1965 an ; 35 ans ; 30 ans.  à t½ la masse initiale de 137Cs est divisée par deux: lecture graphe t½= 35 ans. On considère une substance radioactive qui émet 2 107 particules alpha par seconde et dont la demi-vie est 10 s. Le nombre de noyaux radioactifs dans cette substance est : 2 108 ; 1,4 106 ; 1,4 107 ; 2,9 108. A = 2 107 Bq; A= lN avec l = ln2 / t½ = 0,7 / 10 = 0,07 s-1. N= A/l =2 107 / 0,07 = 2/7 109 = 2,9 108 noyaux.   Données : plomb 82Pb; uranium 92U. L'uranium 238 subit plusieurs désintégrations successives de type a et b - et se transforme en plomb 206. Le nombre de désintégrations de chaque type pour passer de l'uranium 238 au plomb 206 est :  A- 8 désintégrations de type a et 6 désintégrations de type b -. B- 6 désintégrations de type a et 8 désintégrations de type b -. C- 8 désintégrations de type a et 1 désintégrations de type b -. D- 4 désintégrations de type a et 3 désintégrations de type b -. 23892U--> 93AX + -10e Z augmente de1 et A est constant 23892U--> 91234Y + 24He Z diminue de 2 et A diminue de 4. or 238-206 = 32 donc 8 désintégrations a. 8 désintégrations a entraînent une diminutions de 16 pour Z or Z diminue seulement de 92-82 = 10 ; donc 6 désintégrations b -. A vrai Le diagramme énergétique de l'atome de sodium est donné. 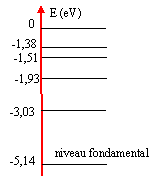On considère un atome de sodium non excité. h= 6,62 10-34 Js ; c= 3 108 m/s ; e = 1,6 10-19 C; raie jaune du sodium l= 589 nm ; Les photons visibles ont des énergies comprises entre 1,6 et 3,1 eV. A- l'énergie d'ionisation de l'atome de sodium vaut 8 10-19 J. B- La transition entre les niveaux -1,93 eV et -5,14 eV correspond à une radiation UV. C- Lorsque l'atome de sodium absorbe de l'énergie, son énergie diminue. D- La transition entre les niveaux - 1,93 et -1,51 eV correspond à une radiation du système visible. 5,14*1,6 10-19 = 8,2 10-19 J E= 5,14-1,93 = 3,21 eV; 3,21*1,6 10-19 = 5,14 10-19 J l = hc/E =6,6 10-34 *3 108 / 5,14 10-19 = 3,85 10-7 m = 385 nm (U.V) E= 1,98-1,51 = 0,42 eV valeur située hors de l'intervalle [1,6 ; 3,1 eV] des énergies des photons du domaine visible. A et B vrais Le spectre d'émission de l'atome d'hydrogène présente plusieurs raies d'émission dans le visible. Les longueurs d'onde exprimées en nm corespondant aux transitions sont : 656 nm ; 486 nm ; 434 nm ; 410 nm. le niveau fondamental est situé à -13,6 eV. A- L'énergie de l'atome d'hydrogène est quantifiée. B- La raies à 656 nm est celle des photons émis de plus faible énergie. C- Si l'énergie apportée à l'atome d'hydrogène est supérieure à 13,6 eV, l'atome est ionisé. D- La lumière émise par l'hydrogène est rouge.  l = hc/DE ; l est d'autant plus grand que DE est plus petit. la lumière émise correspond à un spectre de raies d'émission 656 nm ( jaune) ; 486 nm 434 nm et 410 nm (vet bleu violet) A, B et C vrais

chimie   On dose 100 mL d'une solution d'hydroxyde de sodium (placée dans un bécher ) par une solution d'acide chlorhydrique ( placée dans la burette). On place un conductimètre dans le bécher et on mesure la conductance G au cours du dosage. On néglige l'effet de dilution.l(H3O+)= 35 10-3 S.I ; l(HO-)= 20 10-3 S.I ; l(Na+)= 5 10-3 S.I ; l(Cl-)= 8 10-3 S.I ; A- On obtient la courbe suivante qui représente l'évolution de G en fonction du volume de solution d'acide chlorhydrique versé.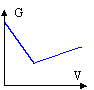 B-Après l'équivalence, l'avancement de la réaction de dosage ne cesse d'augmenter C- A l'équivalence on obtient une solution de chlorure de sodium D- Après l'équivalence le réactif titré devient le réactif limitant. Na+ et HO- dans le bécher ; ajout H+ et Cl- ; H+ + HO- --> H2O avant l'équivalence : cela revient à remplacer HO- par Cl- ; or l(Cl-)<l(HO-) donc la conductivité s diminue dans le bécher après l'équivalence on ajoute H+ par Cl- donc s augmente de plus s et la conductance G sont proportionnelles. A, C et D vrais   L'ion fer II peut être oxydé par l'ion permanganate en milieu acide. On utilise cette réaction pour doser une solution contenant des ions fer II. Couples redox : MnO4- / Mn2+ ; Fe3+ / Fe2+. A- L'équation bilan de la réaction de dosage est : MnO4-+ 5 Fe2++ 8H+--> Mn2+ +5 Fe3++4H2O B- On a à l'équivalence la relation n(MnO4-)versé = 5 n( Fe2+) dosé. C-Avant l'équivalenc, le bécher contenant les ions fer II est de couleur rose violacée. D- A l'équivalence, la quantité de matière initiale du réactif titré est égale à la quantité de matière introduite du réactif titrant. 5 fois{ Fe2+ = Fe3+ + e-} oxydation MnO4- + 8H+ + 5 e- = Mn2+ + 4H2O réduction MnO4-+ 5 Fe2++ 8H+--> Mn2+ +5 Fe3++4H2O MnO4- ajouté + 5 Fe2+. initial 0 nFe2+ en cours x n( Fe2+) -5x équivalence n(MnO4-) = xéqui n( Fe2+) -5xéqui = 0 xéqui = n(MnO4-) = n( Fe2+) /5. avant l'équivalence la solution dans le bécher est incolore ( Fe2+ en excès) ; après l'équivalence la solution est violette (MnO4- en excès. A vrai   On dispose d'une solution aqueuse de chlorure de fer III. On mesure la conductance de cette solution à l'aide d'une cellule conductimétrique, constituée de 2 électrodes parallèles de surface S, distantes de L. A- La conductivité de la solution est donnée par la relation : s = l(Cl-)[Cl-]+3l(Fe3+)[Fe3+]. B- La conductance est donnée par G= s S/L. C- La conductivité dépend de la température de la solution. D- En changeant de conductimètre, on obtient la même valeur de la conductance qu'avec le premier. s = l(Cl-)[Cl-]+l(Fe3+)[Fe3+] avec 3 [Fe3+] = [Cl-] G (S) = s (S m-1) S ( m²) / L (m) en changeant de cellule de mesure on modifie S/L, donc G. B et C vrais   La conductivité d'une solution saturée d'hydroxyde de zinc (Zn2+ + 2HO-) vaut s =2 10-4 Sm-1. l(Zn2+) = 10 10-3 S.I ; l(HO-)= 20 10-3 S.I ; A- La conductivité molaire ionique est donnée en Sm² mol-1. B- La solubilité de l'hydroxyde de zinc est donnée par la relation : s = s / (2l(Zn2+)+l(HO-)) C- La solubilité de l'hydroxyde de zinc est s = 4 10-3 mol /L. D- La solubilité de l'hydroxyde de zinc est s = 5 10-3 mol /L. s = l(Zn2+)[Zn2+] +l(HO-)[HO-] avec s =[Zn2+] et 2 [Zn2+] = [HO-] s = [l(Zn2+) +2l(HO-)]s soit s = s /[l(Zn2+) +2l(HO-)]= 2 10-4 / (10+2*20)10-3]= 4 10-3 mol m-3. A vrai   Expérience 1 : on ajoute de la poudre d'argent en excès à une solution de nitrate de fer (III) de concentration c= 0,01 mol/L. On agite le système jusqu'à ce que l'équilibre soit atteint. Les concentrations des espèces dissoutes valent alors : [Fe3+]éq=3,3 10-4 mol/L ; [Fe2+]éq=[Ag+]éq=0,01 mol/L. Expérience 2 : on introduit dans un bécher une solution de nitrate de fer (III), une solution de nitrate de fer (II°, une solution de nitrate d'argent et un peu de poudre d'argent. Le volume final de la solution est égal à 1 L. On donne les concentrations initiales des espèces chimiques dans le mélange [Fe3+]i=4 10-5 mol/L ; [Fe2+]i=0,012 mol/L et [Ag+]i=3 10-3 mol/L A- L'expérience 1 permet de calculer la constante d'équilibre K de la réaction. sa valeur est 0,3. B- L'expérience 1 permet de conclure que le quotient initial de la réaction est nul. C-Dans l'expérience 2, la masse d'argent solide va augmenter. D- Dans l'expérience 2, la masse d'argent solide va diminuer. Fe3+ + Ag = Fe2+ + Ag+. K = [Fe2+]éq[Ag+]éq/[Fe3+]éq= 0,01² / 3,3 10-4 = 0,3. expérience 1 : Qr,i = [Fe2+]i[Ag+]i/[Fe3+]i= 0 ; expérience 2 : Qr,i =0,012*3 10-3 / 4 10-5 = 1,2*3/4 = 0,9 valeur supérieure à K , donc délacement dans le sens indirect : formation Ag. A, B, C vrais   La charge d'une mole d'électrons est 96500 C. On considère une pile alcaline dont l'équation de la réaction de fonctionnement global est : Zn(s) + 2MnO2(s)+H2O--> ZnO(s) + 2MnO2H(s). On appelle capacité en charge la valeur Qmax de la quantité d'électricité débitée par la pile. Elle vaut 48250C. A- La quantité d'électrons débités par la pile est de 2. B- La quantité d'électrons débités par la pile est de 0,5. C- La quantité de zinc consommé est 0,25 mol. D- La quantité de zinc consommé est 1 mol.Ag. n e- = 48250 / 96500 = 0,2 mol d'électrons Zn + 2HO- = ZnO + H2O + e- d'où nZn = ½ n e- = 0,25 mol. B, C vrais   A- Dans un électrolyseur, le courant entre par l'anode. B- Dans un électrolyseur, le courant entre par la cathode. C- Lors de la décharge, un accumulateur joue le rôle de récepteur. D- Lors de la décharge, un accumulateur joue le rôle de générateur. A, D vrais   Couples oxydant / réducteur : O2/H2O ; H2O/H2 ; Pb2+ / Pb ; H+ / H2. On effectue l'électrolyse de nitrate de plomb en utilisant des électrodes inattaquables de graphite. Les ions nitrates sont indifférents. Il se dépose du plomb à la cathode et il se forme un gaz incolore à l'anode. L'intensité du courant est constante, égale à 1,2 A. La durée du fonctionnement de l'électrolyse est de 20 min. A- Le gaz incolore est le dioxygène. B- Le gaz incolore est le dihydrogène. C- La quantité de plomb déposé est d'environ 15 mmol. D- La quantité de plomb déposé est d'environ 7 mmol. à l'anode oxydation de H2O : H2O = ½O2 + 2H+ + 2e-. à la cathode réduction de : Pb2+ + 2e- = Pb. Q= I t = 1,2* 20*60 = 1440 coulombs ; n e- = 1440 / 96500 = 0,015 mol soit 15 mmol donc nPb = 7,5 mmol A, D vrais   On dissout un acide AH faible dans l'eau pour réaliser une concentration égale à c= 0,1 mol/L. On mesure t le taux d'avancement final de la réaction de dissolution dans l'eau t = 0,01. A- La constante d'équilibre de la réaction vaut K= 10-5. B- Si la concentration de l'acide augmente alors t augmente. C- La valeur du quotient de réaction dans l'état d'équilibre est indépendant de la concentration de l'acide. D- Le pH est supérieur à 5. K = [A-]éq[H3O+]éq / [AH]éq=t² c / (1-t) = 10-4 *0,1 / (1-0,01 ) = 10-5. K ne dépend que de la température ; à une température donnée si c croît alors t diminue. [H3O+]éq =t c = 0,01*0,1 = 10-3 ; pH=3 A, C vrais   L'ion éthylammonium est un acide faible dont la base conjuguée est l'éthylammine. La réaction de dissolution de cet acide dans l'eau conduit à un équilibre chimique suivant la réaction : C2H5NH3+ + H2O = C2H5NH2 + H3O+. La constante d'équilibre associée à cet équilibre vaut 2 10-11. On donne log 2 = 0,3 ; log 5 = 0,7 ; Ke = 10-14. A- Le pka du couple ion éthylammonium / éthylammine vaut environ 11. B- L'éthylamine réagit avec l'eau pour donner une solution basique. C- la constante d'équilibre de la réaction de l'éthylamine avec l'eau vaut 5 10-4. D- La réaction entre l'éthylamine et l'acide chlorhydrique ne peut pas être considérée comme totale. K = [C2H5NH2]éq[H3O+]éq / [C2H5NH3+]éq= 2 10-11 ; log Ka = log 2-11 ; -logKa = pKa = -0,3+11 = 10,7 C2H5NH2 + H2O =C2H5NH3+ + HO- ; K1 =[HO-][C2H5NH3+] / [C2H5NH2]=[HO-] [H3O+] [C2H5NH3+] / ([C2H5NH2][H3O+])= 10-14 / 210-11 = 5 10-4. C2H5NH2+ H3O+-->C2H5NH3+ ; K2 =[C2H5NH3+] / ([C2H5NH2][H3O+])= 1/K = ½ 1011. A, B, C vrais   On dissout dans 500 mL d'une solution d'acide éthanoïque de concentration c1 = 0,1 mol/L et de pH=1,9, une quantité égale à 0,05 mol d'éthanoate de sodium solide. Le pka du couple acide éthanoïque / ion éthanoate vaut 4,8. A- Le pH de la solution diminue après dissolution. B- Les ions éthanoates réagissent avec les ions oxonium de la solution acide. C- Le pH augmente après la dissolution. D- Le pH reste égal à 4,8. CH3COOH initial : 0,05 mol CH3COOH + H2O=CH3COO- + H3O+ ; K = [CH3COO-]éq[H3O+]éq / [CH3COOH]éq= 10-4,8 ; si on ajoute 0,05 mol d'ion CH3COO-, déplacement de l'équilibre vers la gauche. conservation de l'élément carbone : [CH3COO-] + [CH3COOH] = (0,05 +0,05) / 0,5 = 2 mol/L solution électréquiment neutre : [CH3COO-] + [HO-] = [Na+] + [H3O+] [HO-] négligeable en milieu acide ; [CH3COO-] voisin [Na+] + [H3O+] = 0,05 / 0,5 +[H3O+] = 0,1 + [H3O+] 0,1 >> [H3O+] d'où [CH3COO-] voisin 0,1 et [CH3COOH] voisin 0,1 mol/L d'où pH fin proche de pKa = 4,8. B, C vrais   On dose 400 mL d'une solution d'ammoniaque de concentration inconnue par 100 mL d'une solution d'acide chlorhydrique de concentration c= 0,1 mol/L. Ces proportions correspondent à l'équivalence. pKa (NH4+ / NH3)=9,1. A- La réaction de dosage peut être considérée comme totale. B- A l'équivalence 0,02 mol d'ammoniac ont réagi. C- Après avoir versé 50 mL d'acide le pH vaut 4,5. D- Le quotient initial de la réaction s'effectuant dans le mélange précédent est supérieur à la constante d'équilibre de cette réaction. NH3 + H3O+ --> NH4+ + H2O ; K = [NH4+]/([H3O+] [NH3])=1/ Ka = 109,1 ; à l'équivalence : 0,1 * 0,1 = 0,01 mol d'acide versé= 0,01 mol d'ammoniac ayant réagi NH3 H3O+ versé NH4+ initial n= 0,01 mol 0 0 en cours ( x= 0,005) 0,01 -x= 0,005 mol x = 0,005 mol 0,005 mol équivalence 0 0,01 mol 0,01 mol après avoir versé 50 mL d'acide on se trouve à la demi-équivalence et pH=pKa = 9,1 Qr,i = [NH4+]i/([H3O+]i [NH3]i) est inférieure à K car la réaction évolue dans le sens direct. A vrai   On mélange une solution aqueuse de peroxyde d'hydrogène avec une solution aqueuse d'iodure de potassium Le peroxyde d'hydrogène du couple H2O2/H2O oxyde l'ion iodure du couple I-/I2 en diiode, en milieu acide.Le diiode en solution présente un maximum d'absorption à lmax= 350 nm. A cette longueur d'onde, le coefficient d'exctinction molaire e= 2,5 105 mol-1 L cm-1. Dans une cuve d'un spectrophotomètre, de 1 cm de large, on introduit 3 mL d'une solution d'iodure de potassium acidifié, de concentration [I-]=0,01 mol/L puis un volume V=0,5 mL d'une solution de peroxyde d'hydrogène de concentration [H2O2] = 5 10-5 mol/L. On relève les valeurs de l'absorbance A pour lmax= 350 nm et on trace la courbe des variations de [I2] en fonction du temps. t(min) 0 1 3 5 8 10 15 20 30 A 0 0,401 0,945 1,29 1,52 1,63 1,72 1,77 1,78 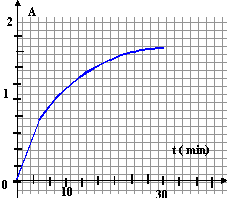A- La quantité maximale de diiode que l'on peut obtenir est de 7,1 10-6 mol/L. B- La quantité maximale de diiode est obtenue à la date 30 min. C- Le temps de demi-réaction est atteint au bout de 30 min. D- Le temps de demi-réaction est atteint au bout de 15 min. à t = 30 min la réaction peut être considérée comme presque terminée. H2O2 + 2I-+ 2H+ --> I2 + 2H2O H2O2 + 2I- I2 initial 5 10-4 * 5 10-5 = 2,5 10-8 mol 3 10-3 *0,01 = 3 10-5 mol 0 en cours 2,5 10-8 -x 3 10-5 -2x x fin 2,5 10-8 -xm xm=2,5 10-8 mol 3 10-5 -2xm = 0 excès xm=2,5 10-8 mol [I2]=2,5 10-8/ 3,5 10-3 = 7,1 10-6 mol/L à t½ la moitié du réactif limitant a disparu : [I2]= 3,6 10-6 mol/L et A =e L [I2] = 2 105 *1*3,6 10-6 =0,71 soit t½ voisin de 3 min. A, B vrais   suite du n°13. A- La vitesse volumique de la réaction peut se mettre sous la forme v=kA avec k une constante. B- La vitesse volumique de la réaction est proportionnelle à la dérivée de l'absorbance par rapport au temps. C- A la date t=0, la vitesse volumique de la réaction et l'absorbance sont minimales. D- A la date t = 30 min, la vitesse volumique de la réaction est quasiment nulle. v = 1/V dx/dt = d[I2] /dt avec [I2] =A/(e L) soit v = 1/(e L) dA/dt à t = 0, le coefficient directeur de la tangente à la courbe A=f(t) est le plus gand possible, donc la vitesse initiale est maximale à t >30 min, la tangente à la courbe est presque horizontale, donc la vitesse est quasiment nulle B, D vrais   L'hydrolyse basique des huiles végétales : A- permet d'obtenir du propan-1,2,3- triol. B- libère de l'eau. C- doit être réalisée à chaud. D- utilise uniquement des solutions aqueuses d'hydroxyde de sodium. libére un ion carboxylate soude ou potasse KOH A, C vrais   Pour une transformation chimique non totale et catalysable : A- Le catalyseur augmente le taux d'avancement final. B- Le catalyseur augmente le temps de demi-réaction. C- Le catalyseur modifie la constante de la réaction. D- Le catalyseur intervient sur la réaction inverse. Le catalyseur permet d'atteindre plus rapidement l'équilibre sans changer ce dernier B, D vrais

retour - menu