concours kiné Nantes 03 physique 1 h - chimie ½ h

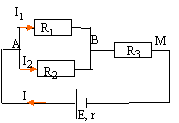
calcul d'intensité (4 points ) R1 = 60 W ; R2 = 40 W ; R3 = 30 W ; E=9 V ; r=6 W.   Calculer les intensités I, I1, I2.   corrigé résistance équivalente à R1 et R2 montées en dérivation : R4 = R1 R2 / (R1 + R2 R4 = 60*40 / 100 = 24 W. résistance équivalente à R4 et R3 montées en série : Réq = 24+30 = 54 W. intensité : I= E / (Réq +r) = 9/(54+6)= 0,15 A. UBM = R3 I = 30*0,15 = 4,5 V ; UAM = E-rI = 9-6*0,15 = 8,1 V ; UAB = 8,1-4,5 = 3,6 V UAB =R1 I1 d'où : I1 =3,6 / 60 = 0,06 A ; UAB =R2 I2 d'où : I2 =3,6 / 40 = 0,09 A .

chute verticale dans un liquide (8 points) Une bille de masse m= 11,3 g et de rayon r = 1 cm est lâchée sans vitesse initiale du haut d'une colonne liquide de hauteur h =2m, de masse volumique r0=1003 kg/m3 et de viscosité h=0,1 SI. La durée de la chute est t1 = 1,03 s. On repère le mouvement du centre de gravité G de la bille sur un axe vertical , vers le bas; lorigine est située à la partie supérieure du liquide.( ce qui est écrit en gras et en bleu est un vecteur) On note A= -m0g la poussée d'Archimède exercée par le liquide . Exprimer m0 en fonction de r et r0. Calculer m0. On néglige la force de frottement fluide. - Montrer que le mouvement serait uniformément accéléré. - Quelles seraient la durée t2 de la chute et la vitesse v2 d'arrivée en bas de la colonne ? On considère que la bille animée d'une vitesse v est soumise à une force de frottement fluide f = -6 pr hv - Etablir l'équation différentielle en v(t). - Vérifier que la solution de l'équation différentielle est de la forme v(t) = vlim (1-e-t/t). - Que représentent vlim et t ? Tracer v en fonction de t. - Calculer la vitesse v après une durée de chute égale à t2. Vérifier que z(t) est de la forme z = at+be-t/t+g où a, b, g sont des constantes à déterminer. On notera qu'à t=0, z=0. - calculer z aux dates t1 et t2 et conclure. g = 9,81 m/s².   corrigé poussée = poids du volume de liquide déplacé = 4/3 p r3r0g volume du liquide déplacé : 4/3 p r3 ; masse de ce liquide : m0 = 4/3 p r3r0g = 4/3*3,14 (10-2)3*1003 = 4,2 10-3 kg. poids : P=mg = 11,3 10-3 *9,81 = 0,11 N. La deuxième loi de Newton s'écrit sur un axe vertical dirigé vers le bas : mg -m0g = ma soit a = g(1-m0/m) = 9,81(1- 4,2/11,3) = 6,16 m/s² ; mouvement rectiligne uniformément accéléré. h = ½at2² d'où t2² = 2h /a = 2*2 / 6,16 = 0,65 s² soit t2 = 0,806 s. v finale = at2 = 6,16*0,806 = 4,96 m/s². La deuxième loi de Newton s'écrit sur un axe vertical dirigé vers le bas : mg -m0g -6 pr hv= ma = mdv/dt = mv' v' + 6 pr h / m v = g(1-m0/m) (1) dériver l'expression de la vitesse v par rapport au temps : v = vlim (1-e-t/t). ; v' = vlim / t e-t/t ; repport dans (1) : vlim / t e-t/t +6 pr hvlim / m (1-e-t/t)= g(1-m0/m) vlim e-t/t [1/t -6 pr h/ m)+6 pr hvlim / m ]= g(1-m0/m) l'expression proposée pour la vitesse est solution de (1) si : [1/t -6 pr h/ m)+6 pr hvlim / m ]= 0 soit : t = m / (6 pr h) = 11,3 10-3 / (6*3,14*0,1 10-2)=0,6 s. et 6 pr hvlim / m ]= g(1-m0/m) d'où vlim = g(m-m0)/(6 pr h) = 9,81(11,3-4,2)10-3 / (6*3,14*0,1 10-2)=3,7 m/s. t est la constante de temps ; la vitesse limite est atteinte au bout d'une durée supérieure ou égale à 5 t. 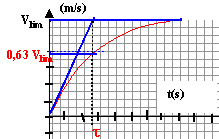v'2 = vlim (1-e-t2/t) = 3,7(1-e-0,806 / 0,6)=3,7(1-e-1,34) = 3,7(1-0,26)=2,74 m/s. z(t) est une primitive de v(t) : v(t) = vlim -vlime-t/t ; z(t) = vlim t - vlim (-t) e-t/t + constante = vlim t + vlim t e-t/t + constante. d'où a = vlim = 3,7 m/s ; b = vlim t = 3,7*0,6 = 2,22 m ; z(t=0 ) = vlim t e-0 + constante d'où constante = g = -vlim t = -2,22 m ; z(t) = 3,7 t + 2,22 e-t/t -2,22. z(t= 1,03 s) = 3,7 * 1,03 +2,22 e-1,03 / 0,6 -2,22 = 1,99 m. z(t= 0,806 s) = 3,7 * 0,806 +2,22 e-0,806 / 0,6 -2,22 = 1,32m. à t=t1, la bille est arrivée en bas de la colonne liquide ; la force de frottement fluide est négligeable devant la poussée sur une distance de chute de deux mètres. à t = t2 la vitesse limite n'est pas encore atteinte.

radioactivité (8 points) A. Le polonium 210(21084Po ) est un nucléide a ; le noyau fils est un isotope du plomb AZPb. Ecrire l'équation de cette désintégration radioactive et déterminer A et Z. Calculer l'énergie Q libérée par la désintégration d'un noyau de polonium 210 ( en J et en MeV). On montre que lors de la désintégration, les vitesses du noyau fils vPb et de la particule a, va sont dans le rapport inverse des masses c'est à dire : vPb / va= ma / mPb. - En déduire l'expression de l'énergie cinétique, Ec(Pb), du noyau fils en fonction de l'énergie cinétique Ec(a) de la particule a et des masses ma, mPb. - Calculer en MeV, l'énergie cinétique de la particule a si la désintégration se fait : * sans émission de photon g. * Avec émission de photon g de longueur d'onde l = 0,565 10-12 m. B.La demi-vie du polonium 210 est t½ = 138 jours. Quelle est sa constante radioactive l ? Un échantillon de polonium 210 a une activité A0=1010 Bq à t=0. Calculer le nombre N0 de noyaux présents dans cet échantillon. Après quelle durée l'activité sera divisée par 4 ? Donner la relation entre A(t) ( activité à la date t) et A0. - Exprimer la diminution relative d'activité r = (A0-A(t)) / A0 en fonction de t½ et de t. - Calculer r pour t=1 jour. Données : m(21058Po ) = 209,98286 u ; m(AZPb ) = 205,97445 u ; ma= 4,00150 u ; 1eV= 1,6 10-19 J; 1 u = 1,66 10-27 kg ; h = 6,63 10-34 Js ; c= 3 108 m/s. corrigé 21084Po --> 42He + AZPb. conservation de la charge : 84 = 2+Z d'où Z= 82 conservation du nombre de nucléons : 210 = 4 + A d'où A= 206. |Dm|= 205,97445+4,00150-209,98286 = 6,91 10-3 u 6,91 10-3 *1,66 10-27 = 1,147 10-29 kg. Q= |Dm|c² = 1,147 10-29*(3 108)² = 1,032 10-12 J. 1,032 10-12 / 1,6 10-19 = 6,45 106 eV = 6,45 MeV. sans émission de photon g : Ec(Pb) =½mPb v²Pb. Ec(a) =½ma v²He Ec(Pb) /Ec(a) = mPb / ma (vPb/ vHe)² = mPb / ma ( ma / mPb)² = ma / mPb Ec(Pb)= ma / mPb Ec(a) avec émission de photon g : énergie du photon E = hc/l = 6,63 10-34 * 3 108 / 0,565 10-12 =3,52 10-13 J 3,52 10-13 / 1,6 10-19 = 2,2 106 eV = 2,2 MeV Q-E = Ec(Pb) + Ec(a) = Ec(a) (1+ma / mPb ) Ec(a) =(Q-E) / (1+ma / mPb ) ; Ec(a) = (6,45-2,2) / 1,00194 = 4,17MeV. lT= ln2 soit l = 1/(138*24*3600)= 5,81 10-8 s-1. A0 = l N0 d'où N0 = 1010/5,8 10-8 = 1,72 1018 noyaux. après deux périodes(2*138 = 276 jours) l'activité est divisée par 2² =4. A = A0 e -lt ; A / A0 e -lt ; 1-A / A0 = 1- e -lt ; (A0 -A)/A0 =1- e -lt ; r = 1- e -lt . or l = ln2 / T d'où e -lt = e-ln2 t/ T = 2 -t/ T soit r = 1-2 -t/ T. r = 1-2-1/138 = 1-2-0,00724 = 1-0,995 = 0,005 (0,5 %)

conductimétrie et réaction acido-basique (3 points) Ecrire l'équation d'autoprotolyse de l'eau et calculer la conductivité s0 de l'eau pure à 25°C. A 25°C la conductivité d'une solution aqueuse d'acide fluorhydrique de concentration c=0,1 mol/L est s = 0,324 S/m. - Ecrire l'équation de la réaction entre l'acide fluorhydrique et l'eau. Donner l'expression de la constante d'acidité Ka correspondante. - Comparer s et s 0 et conclure. - Calculer le taux d'avancement t, à l'équilibre de la réaction de l'acide fluorhydrique avec l'eau. - Quel est le pH de la solution d'acide fluorhydrique ? - Calculer le pKa du couple HF/ F-. Données : conductivité molaire ionique (mS m² mol-1). H3O+ : 35 ; HO- : 19,9 ; F- : 5,5.   corrigé 2 H2O=H3O+ + HO- avec [H3O+]=[HO-]=10-7 mol/L = 10-4 mol/m3 à 25 °C s 0 = [l(H3O+) +l(HO-)]10-4 = (35 +19,9) 10-3 * 10-4 = 5,49 10-6 S/m. HF+H2O=H3O+ + F-avec [H3O+]=[F-] = tc et [HF]=(1-t)c Ka = [H3O+][F-] / [HF]=(tc)² / ((1-t)c) = t²c / (1-t) s est bien supérieur à s 0 : l'acide fluorhydrique est en partie ionisé dans l'eau et on peut négliger les ions oxonium issus de l'autoprotolyse de l'eau devant ceux issus de l'acide. s = [l(H3O+) +l(F-)]tc = (35 +5,5) 10-3 * tc = 4,05 10-2 tc ;or c = 0,1*1000 = 100 mol/m3. s =4,05 10-2 t *100 = 4,05t soit t = s / 4,05 = 0,324 / 4,05 = 0,08 . [H3O+] = tc = 0,08 * 0,1 = 8 10-3 mol/L et pH = -log (8 10-3)= 2,1. Ka =t²c / (1-t) = 0,08 * 0,1² / (1-0,08) = 6,95 10-4. pKa = -log(6,95 10-4)=3,16.

alcènes- alcools - esters (3,5 points)   Donner les formules semi-développées et les noms des alcènes non cycliques de masse molaire M=56 g/mol. L'hydratation du but-1-ène en présence d'acide sulfurique conduit à un mélange de deux alcools A et B que l'on sépare par distillation. Donner la formule semi-développée, la classe et le nom de chaque alcool. A et B sont traités séparément par une solution acidifiée de permanganate de potassium en excès et on obtient A' et B'. A' est un acide carboxylique. B' donne un précipité jaune avec la DNPH mais ne réagit pas avec la liqueur deFehling. - Donner les formules semi-développées et les noms de A' et B'. - Identifier A et B. On fait réagir un mélange équimolaire de A' et de B' en présence d'acide sulfurique. Ecrire l'équation chimique de la réaction. - Nommer les produits obtenus. On donne C=12 ; H=1 g/mol. corrigé formule brute d'un alcène CnH2n ; masse molaire 12n+2n = 56 soit n=4. 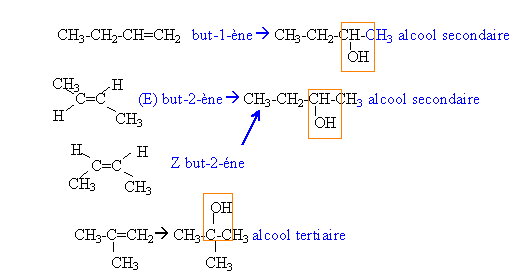B : butan-2-ol CH3-CH2-CH(OH)-CH3 donne la butanone B' (cétone) CH3-CH2-CO- CH3 A : butan-1-ol CH3-CH2-CH2-CH2OH donne l'acide butanoïque A' : CH3-CH2- CH2-COOH CH3-CH2- CH2-COOH +CH3-CH2-CH(OH)-CH3 = CH3-CH2- CH2-COO-CH(CH3)-CH2-CH2-CH3 + H2O nom de l'ester : butanoate de 1-méthylpropyle.

décomposition de l'eau oxygénée (3,5 points) L'eau oxygénée est uns solution aqueuse de peroxyde d'hydrogène H2O2. L'eau oxygénée se décompose lentement suivant la réaction : H2O2 = ½O2 + H2O. Une oxygénée à n volume peut dégager n litres de dioxygène par litre de solution ( volume gazeux mesuré sous la pression p=101,3 kPa et à la température T=273,15 K). - Calculer la concentration en mol/L d'une eau oxygénée à 10 volumes. La décomposition d'une solution de H2O2 est suivie en prélevant rapidement des échantillons de même volume vP à des instants déterminés, et en dosant rapidement la quantité de H2O2 restant au moyen d'une solution de permanganate de potassium de concentration cox, en milieu acide. Les couples redox mis en jeu sont : O2 / H2O2 et MnO4- / Mn2+. - Ecrire l'équation de la réaction de H2O2 et de l'ion permanganate MnO4- . - Comment repère-t-on pratiquement l'éqyuivalence du dosage ? - Donner la relation entre la concentration c de la solution d'eau oxygénée, le volume prélevé vP, cox, et le volume vox de la solution de permanganate nécessaire pour obtenir l'équivalence. Les différents volumes vox de permanganate de potassium nécessaires pour doser les prélevements effectués aux différentes dates sont notées dans le tableau suivant : t en min 0 5 10 20 40 vox mL 30,7 24,7 19,9 13,1 5,5 On montre que l'évolution de c en fonction du temps t suit la loi exponentielle c= c0 e-kt. k est une constante ( constante de vitesse) et c0 est la valeur de c à t=0. - Calculer k (on précisera l'unité) - Partant d'une eau oxygénée à 10 volumes, après combien de temps ontiendra-t-on une eau oxygénée à 5 volumes ? - Calculer la vitesse initiale de décomposition de cette eau oxygénée (préciser l'unité) On donne la constante des gaz parfaits R= 8,314 J K-1 mol-1. corrigé volume molaire Vm= nRT/P = 1*8,314*273,15 / 101300 = 0,0224 m3/mol = 22,4 L/mol. Qté de matière dioxygène : 10/22,4 = 0,446 mol d'où la qté de matière d'eau oxygénée : 2*0,446 = 0,892 mol dans 1L. MnO4- + 8H+ + 5e- = Mn2+ + 4H2O multiplier par 2 . H2O2 = O2 + 2H+ + 2e- multiplier par 5 . 2MnO4- +6H+ + 5H2O2--> 2Mn2+ +5O2 +8H2O l'ion permanganate joue un double rôle : celui de réactif et celui d'indicateur de fin de réaction ( MnO4- violet -->Mn2+ incolore) 5H2O2 2MnO4- ajouté initial VP[H2O2] 0 en cours VP[H2O2]-5x 2x à l'équivalence VP[H2O2]-5xmax=0 2xmax = CoxVox. xmax = ½CoxVox etVP[H2O2]- 2,5CoxVox =0 soit [H2O2] =2,5CoxVox /VP. [H2O2] = constante *Vox =A*Vox . C0 =A*Vox (t=0) et C (t)=A*Vox (t) soit C0 / C (t) =Vox (t=0) /Vox (t) de plus : C= C0 e-kt s'écrit : ln (C0 /C) = kt soit k = 1/t ln (C0 /C) t(min) 0 5 10 20 40 Vox (mL) 30,7 24,7 19,9 13,1 5,5 Vox (t=0) /Vox (t) xxxxxxxxx 1,25 1,54 2,34 5,58 ln(Vox (t=0) /Vox (t)) xxxxxxxxx 0,217 0,433 0,851 1,72 k xxxxxxxxx 0,217/ 5=0,043 0,043 0,0425 0,043 k = 0,043 min-1. la concentration de l'eau oxygénée est divisée par 2 : ½C= C0 e-kt soit ln0,5 = -kt t = ln2 / k = 0,693 / 0,043 =16,12 min. vitesse initiale : dériver C par rapport au temps :C= C0 e-kt ; dC/dt = - kC0 e-kt ; à t=0 cette dérivée vaut : -kC0 soit en valeur absolue kC0. la valeur de la vitesse est, en valeur absolue, le coefficient directeur de la tangente à la courbe C=f(t) à une date donnée. ce coefficient directeur vaut :|- kC0 e-kt | soit kC0 à t=0. kC0 = 0,043 * 0,89 = 0,038 mol L-1 min-1. retour - menu