d'après concours technicien météo 02 durée3 h

solide sur plan incliné Un mobile M peut glisser sans frottement le long de la ligne de plus grande pente x'Ox d'un plan incliné faisant un angle a par rapport au plan horizontal. Il est attaché à un fil inextensible tendu parallèlement à l'axe x'Ox. À l'instant t = 0, le mobile M est au repos au point 0, origine de l'axe, et on applique au fil une traction qui fait gravir à M le plan incliné; à l'instant t = 2,0 s, le fil casse. (Masse du mobile: 0,65 kg.) Un capteur optique, couplé à un ordinateur, mesure la vitesse vx du mobile et donne l'expression de vx (en m.s-1) en fonction du temps t en s. Pour 0< t<=2s alors vx=0,75t ; Pour t>2s alors vx= -2,5 t + 6,5 Quelle distance M a-t-il réellement parcourue entre t=0 et l'instant où il rebrousse chemin? Calculer la valeur de la force de traction avant que le fil ne casse. corrigé distance parcourue sur le plan durant les deux premières secondes : primitive de la la vitesse vx. x= ½ *0,75 t² + Cte à t = 0 , x=0 la constante d'intégration est donc nulle. x= 0,375 t² soit d1 = x(t=2) = 0,375*4=1,5 m. Lorsque le fil casse, le solide continue à monter le plan, du fait de sa vitesse initiale vx(t=2) = 0,75*2 = 1,5 m/s. Puis il s'arrête et rebrousse chemin. la montée est uniformément retardée avec a = -2,5 m/s² du fait que vx= -2,5 t + 6,5 Or a = -g sin a = -2,5 d'où sin a = 2,5 / 9,8 = 0,255 et a = 14,8° Appliquer le théorème de l'énergie cinétique entre l'instant où le fil casse et l'instant ou le solide rebrousse chemin : le solide est soumis à son poids, vertical vers le bas, à la réaction du plan, perpendiculaire au plan en l'absence de frottement. Seul le poids travaille , la tension étant perpendiculaire à la vitesse somme des travaux : Wforces = m a d2 , avec d2 distance parcourue sur le plan le travail du poids est résistant ( signe moins) car on monte le plan. variation d'énergie cinétique : Ec finale -Ec initiale = 0 - ½mv² initiale. m a d2 = - ½mv² initiale soit d2 = ½v² initiale / (-a) = 0,5*1,5 / 2,5 = 0,3 m distance totale : 1,5+0,3 = 1,8 m. force de traction avant rupture : en plus des forces précédentes, le solide est soumise à la force de traction f, parallèle au plan et dirigée vers le haut. travail de ces forces entre l'instant initial et l'instant de la rupture : W = m a d1 avec d1 = 1,5 m et a = 0,75 m/s² soit W= 0,65*0,75*1,5= 0,731 J. ou bien appliquer le théorème de l'énergie cinétique entre l'instant initial et l'instant où le fil casse : Ec finale -Ec initiale = ½mv² finale-0 = 0,5*0,65*1,5² = 0,731 J. travail du poids : -mgd1sin a ; travail de f = f d1 . par suite : -mgd1sin a + f d1 = 0,731. f = 0,731 / d1 +mgsina = 0,731/1,5 + 0,65*9,8*0,255 = 0,487 + 1,624 = 2,11 N.

Satellite Un satellite artificiel (S1) de masse m1 est assimilable à un point matériel. Dans un repère géocentrique, supposé parfaitement galiléen, son orbite est assimilée à un cercle de rayon r de même centre O que celui de la Terre. Le satellite S1 n'est soumis qu'à l'attraction terrestre. Montrer que le mouvement du satellite S1 est uniforme. Etablir littéralement la valeur v1du vecteur vitesse de ce satellite en fonction de la constante de gravitation G, de la masse MT de la Terre et de r. - Calculer numériquement v1sachant que G=6,67×10-11N.m2.kg-2 MT=6×1024kg r=7000km Un satellite(S2) de masse m2, cherche à rejoindre (S1). (S2) se déplace sur la même orbite que (S1) mais à une vitesse de valeur v2 supérieure à v1. - Montrer qu'en plus de l'attraction terrestre le satellite (S2) doit être soumis à une force ; préciser la direction de cette force qui est produite par un petit moteur auxiliaire. - Exprimer littéralement la valeur f en fonction de m2, r, v1 et v2. - Calculer numériquement f, sachant que v2=v1+5 m.s-1 et que m2=2×103kg corrigé Le satellite n'est soumis qu'à la force de gravitation centripète, perpendiculaire à la vitesse à chaque instant ; en conséquence cette force ne travaille pas ; l'énergie cinétique du satellite reste constante ainsi que la norme du vecteur vitesse le mouvement est donc uniforme et circulaire. valeur de la force de gravitation : F= GMTm / r² valeur de l'accélération centripète : aN= v²1 / r la seconde loi de Newton s'écrit sur un axe pointant vers le centre de la terre : GMTm / r² = mv²1 / r d'où v²1 = GMT / r = 6,67×10-11 * 6×1024 / (7 106 )= 5,717 107 soit v1 = 7,561 km/s. La vitesse v1 dépend de la distance du satellite au centre de la terre, quelle que soit la masse du satellite. En conséquence si (S2) se trouve sur la même orbite avec une vitesse différente, il ne peut pas être soumis uniquement à la force de gravitation de la terre. Le mouvement est circulaire, l'accélération est centripète : donc la somme vectorielle des forces est radiale, dirigée suivant un rayon terrestre. Cette somme est centripète car la vitesse v2 est plus grande que v1. Ecrire la seconde loi de Newton sur un axe centripète : f + GMTm2/r²=m2v²2/r Or v²1 = GMT / r d'où f + m2 v²1 /r = m2 v²2/r f = m2 /r (v²2 -v²1 ) =2 103/(7 106 )*5*15127=21,6 N.

électricité On dispose de trois dipôles de nature inconnue numérotés 1, 2 et 3. Chaque dipôle peut être soit un conducteur ohmique de résistance R, soit une bobine de résistance r et d'inductance L, soit d'un condensateur de capacité C. On réalise deux séries de mesures : - On applique à chaque dipôle une tension continue de 12V et on mesure l'intensité correspondante. - On applique à chaque dipôle une tension alternative sinusoïdale de valeur efficace 12V et de fréquence N=50Hz et on mesure l'intensité efficace correspondante. On obtient les résultats suivants : en continu en alternatif sinusoïdal dipôple 1 4,8 A 3,2 A dipôle 2 2,5 A 2,5 A dipôle 3 0 A 5 10-3 A Déterminer, en justifiant la réponse, la nature de chaque dipôle. Quelles sont les résistances du conducteur ohmique et de la bobine ? Si on applique aux bornes d'un condensateur de capacité C, une tension alternative sinusoïdale de la forme u(t)=Umsin(2pNt) où N est la fréquence de la tension, montrer que le courant circulant dans le circuit peut s'exprimer i(t)=Imcos(2pNt). Trouver une relation liant Um, Im, C et N. - En utilisant les résultats numériques ci-dessus déterminer la valeur de la capacité du condensateur utilisé. Dans une autre expérience on charge le condensateur précédent à l'aide d'un générateur de courant d'intensité constante de 2µA. Le condensateur étant initialement déchargé on lui applique le générateur de courant précédent on constate que la tension aux bornes du condensateur est une fonction linéaire du temps dont le facteur de proportionnalité est de 1,54 V.s-1. Retrouver la valeur de la capacité C du condensateur. On associe les trois dipôles en série et on applique , aux bornes de l'ensemble, une tension alternative sinusoïdale de fréquence réglable et de valeur efficace constante de 6V. On mesure l'intensité efficace dans le circuit pour différentes fréquences. L'auto-inductance de la bobine est de 9mH et le facteur de qualité du circuit est de 11,3. Sachant d'autre part que l'une des limites de la bande passante à 3dB est égale à 1530Hz, indiquer l'allure de la courbe de résonance obtenue en précisant les coordonnées du sommet de la courbe et les limites de la bande passante à 3dB.   corrigé le dipôle 2 est un conducteur ohmique ( résistor) car l'intensité est la même en courant continu et en courant alternatif. Le dipôle 3 est un condensateur ; il se comporte comme un interrupteur ouvert en courant continu ( intensité nulle lorsque le condensateur est chargé) en conséquence le dipôle 3 est une bobine inductive. Résistance du conducteur ohmique : 12 / 2,5 = 4,8 ohms. en courant continu la bobine se comporte comme un résistor de résistance r = 12 / 4,8 = 2,5 W. relation entre la charge d'une armature du condensateur et la tension aux bornes de ce dernier : q (coulomb) = C ( farad) * u (volt) relation entre charge et intensité : i = dq/dt (dérivée de la charge par rapport au temps) i = dq/dt = d(Cu)/dt = C du/dt = Cu' Or u(t)=Umsin(2pNt) ; u'(t) = 2pN Umcos(2pNt) ; i(t) = C2pN Umcos(2pNt) avec Im =C2pN Um. C=Im / (2pN Um)=Iefficace / (2pN Uefficace)=5 10-3 / (6,28*50*12)=1,32 10-6 F. charge avec un générateur de courant : d'une part q=Cu et d'autre part q=i t ( i est constant) d'où u= i/C t avec i / C= 1,54 Vs-1 et i = 2 10-6 A C =2 10-6 / 1,54 =1,3 10-6 F. à la résonance , l'impédance du circuit est minimale, égale à la somme des résistance du circuit d'où Ieff maxi = 6 / (4,8 + 2,5 )= 0,82 A. pulsation propre w0²= 1/(LC) =1/(9 10-3* 1,32 10-6 )=8,42 107. w0=9,175 103 rad/s ; fréquence propre f0= w0/(2p) =9,175 103 / 6,28 = 1461 Hz. facteur de qualité Q = f0/Df avec D f bande passante ( ensemble des fréquences telles que l'intensité soit supérieure à la valeur maximale de l'intensité divisée par racine carrée de 2) d'où D f =f0/Q = 1461 / 11,3= 129 Hz D f = f2-f1 =129 avec f2 = 1530 Hz d'où f1 =1401 Hz.

champ magnétique   La valeur du champ magnétique créé dans la région centrale d'un solénoïde de longueur L, de diamètre d , comprenant N spires et parcouru par un courant I est égal à B1=m0 NI / (d²+L²)½ avec µo=4p×10-7 S.I. -Quelle doit être la valeur maximale du rapport d/L pour que cette valeur diffère de moins de 2% de la valeur approximative donnée par B=µoNI/L Un solénoïde horizontal comporte 1500 spires réparties sur une longueur de 0,8m, son diamètre vaut 5cm. Il renferme dans sa région centrale une aiguille aimantée, placée sur pivot. Initialement l'axe horizontal du solénoïde est dans le plan du champ magnétique terrestre du lieu où est réalisée l'expérience. - Calculer l'intensité I0 du courant qui doit passer dans le solénoïde pour que le champ magnétique créé par le solénoïde dans sa région centrale ait la même valeur que le champ magnétique terrestre soit BT=2.10-5T. - On veut créer dans le solénoïde une zone où le champ magnétique soit nul. Faire un schéma indiquant la position du solénoïde et le sens du courant qui le parcourt. Quelle orientation prend alors l'aiguille aimantée. - Le solénoïde conservant la position précédente, on modifie l'intensité du courant sans changer le sens : I=2I0. Quelle position l'aiguille aimantée prend-t-elle ? De quel angle doit-on faire tourner le solénoïde autour de son axe pour que l'aiguille tourne de 90° ?   corrigé écart 2% signifie : (B-B1)/B<= 0,02 ou bien 1-B1/B < = 0,02 soit B1/B > 0,98 avec B1=m0 NI / (d²+L²)½ et B=µoNI/L soit B1/B = L / (d²+L²)½ L / (d²+L²)½ >0,98 élever au carré : L² / (d²+L²) >0,98² 1/ (d²/L²+1)>0,96 soit 1 >0,96(d²/L²+1) 1>0,96*d²/L² +0,96 soit 0,04 >d²/L² ou d/L <0,2. B=µoNI0/L = 4p×10-7 *1500I0 / 0,8 = 2 10-5. 235,5 I0 =2 soit I0= 8,5 mA. 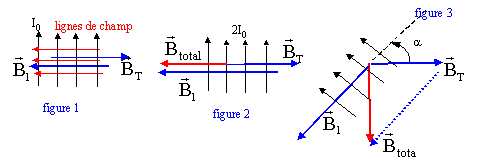Si le champ est nul alors l'aiguille aimantée conserve la position quelconque qu'on lui donne.(figure 1) Si l'intensité double alors le champ crée par la bobine double (figure 2): l'aiguille aimantée s'oriente suivant le champ total. Le champ magnétique résultant est perpendiculaire à l'axe horizontal, puisque l'aiguille aimantée a tourné de 90°. (figure 3) La bobine tourne alors d'un angle a tel que : cos a = BT / B total = 0,5 a = 60°.

retour - menu