d'après concours officiers de 1ère classe de la marine marchande 03 physique 3 h - avec calculatrice.

chute d'une balle (6 points) On étudie la chute d'une balle de tennis, de masse m= 60 g, de dimètre 6,8 cm de volume V0. A la date t=0, la balle est lâchée sans vitesse initiale d'un point O, pris comme origine de l'axe vertical z'z, orienté vers le bas. On relève les positions successives du centre d'inertie G de la balle. g=9,81 m/s² Dans cette partie on néglige l'influence de l'air. - Donner les deux forces que l'on néglige dans ce cas. - A partir de la seconde loi de Newton, établir l'expression de la valeur de la vitesse v en fonction du temps. Tracer le diagramme v= f(t) entre les dates t=0 et t= 3,2 s. On réalise l'expérience et on obtient les résultats suivants : z (m) 0 1 3 5 7 9 11 15 20 30 40 t(s) 0 0,45 0,79 1,02 1,22 1,39 1,55 1,82 2,14 2,69 3,2 v (m/s) 0 4,4 7,4 9,5 11,1 12 13,1 15,2 17,3 19,3 21,4 - Sur le graphe précédent, avec la même échelle, tracer la courbe v=f(t) à partir des résultats expérimentaux. - Donner la variation quantitative de l'accélération du centre d'inertie de la balle au cours du mouvement. - Lors de la chute, il faut tenir compte des forces dues à l'influence de l'air : la Poussée d'Archimède P dont la valeur est constante au cours de la chute ; une force de frottement f proportionnelle au carré de la vitesse f= bv², b est une constante qui dépend des caractéristiques de l'objet et du milieu dans lequel il se déplace. Calculer la valeur de la poussée d'Archimède ( masse volumique de l'air rair = 1,3 kg/m3). Montrer que cette force est négligeable devant le poids de la balle. Volume d'une sphère 4/3 p R3. - Montrer que l'application de la 2ème loi de Newton conduit à une équation de la forme : dv/dt = g(1-v²/V²) en posant V²= mg/b. - A l'aide de l'analyse dimensionnelle montrer que V a les dimensions d'une vitesse. Calculer V si b = 10-3 kg m-1. - Donner la valeur de l'accélération lorsque la vitesse atteint la valeur V. - Donner la nature du mouvement. corrigé On néglige la poussée d'Archimède P= rair V0 g et la force de frottements sur les couches d'air. v= gt = 9,81 t ; v(t=3,2 ) = 9,81*3,2 = 31,4 m/s.   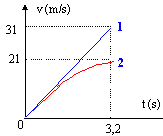courbe 2 : le coefficient directeur de la tangente à cette courbe donne l'accélération: or la tangente est de plus en plus horizontale lorsque la vitesse se rapproche de la valeur limite.Le coefficient directeur, donc l'accélération va décroîte de 9,8 à zéro. volume de la balle V0 = 4/3pr3 = 4/3*3,14*(3,4 10-2)3 = 1,64 10-4 m3. P= rair V0 g = 1,3*1,64 10-4 *9,81 = 2,1 10-3 N. poids : mg = 0,06*9,81 = 0,59 N oit 280 fois plus grand que la poussée : cette dernière est négligeable devant le poids. La balle est alors soumise à deux forces : le poids verticale vers le bas et la force de frottement, verticale vers le haut. La seconde loi de Newton s'écrit suivant un axe verticale vers le bas : mg -bv² = mdv/dt ou g -b/m v² = dv/dt g[1- b/(mg) v²]=dv/dt avec V² = mg / b analyse dimentionnelle : mg : force en newton b: force / vitesse ² et 1/ b: vitesse ² / force mg / b : force fois vitesse ² / force donc homogène à une vitesse au carré. V a donc la dimension d'une vitesse. V= (0,06*9,81 / 10-3)½ = 24,26 m/s. Lorsque la vitesse atteint la valeur limite V le mouvement devient rectiligne uniforme et l'accélération s'annule.

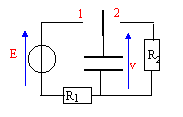
Décharge d'un condensateur (6 points) L'interrupteur K est placé depuis longtemps en position 1. L'instant initial correspond au basculement de l'interrupteur. Expliquer pourquoi l'interrupteur est d'abord placé en position 1. - Donner le phénomène étudié en basculant l'interrupteur en position 2. Donner, en fonction de R, C, v= uC, l'expression de la tension uR aux bornes du conducteur ohmique. En utilisant la loi d'additivité des tensions, établkir l'équation différentielle du premier ordre vérifiée par la tension uC. La solution de cette équation différentielle est du type : uC(t)= Aekt+B où A et B sont des constantes. - Déterminer A et B à partir des conditions initiales. - Déterminer l'expression de la constante k en fonction des paramètres du circuit. Donner alors l'expression de la tension aux bornes du condensateur. Donner l'allure de la courbe représentative de la fonction uC = f(t). Déterminer le coefficient directeur de la tangente à la courbe à un instant t quelconque. Montrer que l'équation de la tangente à la courbe, à l'instant t=0 a pour forme : y = -E/(RC) t + E En déduire l'expression de l'abscisse t du point d'intersection de la tangente à l'origine avec l'axe des abscisses. corrigé interrupteur en position 1 : charge du condensateur; en fin de charge uC=E. en position 2 : décharge du condensateur à travers le résistor R uC=uR =Ri ; i = -dq/dt= -CduC/dt = -Cu'C. ( signe moins car décharge) uC=-RCu'C soit u'C+(RC)-1uC=0 avec t = RC, constante de temps du dipôle RC. à l'instant initial (t=0) où l'interrupteur bascule en position 2 : uC=E = Ae0+B=A+B à linstant final ( condensateur déchargé ) : uC=0 ; k étant négatif, le facteur ekt s'annule.0 = A*0 +B soit B=0 et par suite A=E uC=Eekt = Ee-t/(RC) = Ee-t/t. coefficient directeur de la tangente à la courbe : dériver uC par rapport au temps : u'C= E(-RC)-1 e-t/(RC). à t=0 : u'C(t=0)=E(-RC)-1 . la tangente à l'origine passe par le point (0; E) d'où son équation : y = E(-RC)-1t +E intersection de la tangente à l'origine avec l'axe des temps : y=0 soit 0= -E / (RC) t + E ; 0 = t /(RC) +1d'où t = RC.

radioactivité (4 points) Un laboratoire reçoit un échantillon de 1 mg de cadmium radioactif 10748Cd, de demi-vie t½=6 h 42 min. Il se désintègre en 10747Ag avec émission d'une particule chargée. Ecrire l'équation de désintégration en la justifiant par les lois de conservation. Donner la nature de la particule émise. La désintégration du cadmium10748Cd s'accompagne de l'émission d'un rayonnement g. Donner la anture physique de ce rayonnement. Expliquer son émission. Définir la constante radioactive l . Donner son expression et la calculer. Calculer le nombre N0 de noyaux présents au moment de la réception de l'échantillon. Définir l'activité à la date t d'un échantillon radioactif contenant N(t) noyaux. Calculer l'activité de cet échantillon étudié à la date t=0. Calculer la durée au bout de laquelle l'activité aura diminué des trois quart. N= 6,02 1023 mol-1.   corrigé 10748Cd --> 10747Ag* + AZX conservation de la charge : 48 = 47+Z d'où Z=1 conservation du nombre de nucléons : 107=107+A soit A=0 ; la particule X est un positon, électron positif il s'agit de la radioactivité b+. l'atome fils excité revient à son état fondamental en libérant de l'énergie sous forme de photon g, rayonnement électromagnétique de même nature que la lumière mais plus énergétique. 10747Ag* -->10747Ag + 00g. l= ln2 / t½ ; t½= 6*3600+42*60 = 24120 s ; l=ln 2 / 24120 = 2,873 10-5 s-1. N0 = masse (g) / masse molaire Cd * nombre d'Avogadro = 10-3 / 107*6,02 1023 = 5,626 1018 noyaux initiaux. activité A=lN ; A0=lN0 = 2,873 10-5 * 5,626 1018 = 1,616 1014 Bq. A=A0 e-lt soit ln (A0/A) = l t ; l'activité résiduelle est égale à l'activité initiale divisée par 4 : ln (A0/A) = - ln 0,25 = 1,396 t = 1,396 / l = 1,396 / 2,873 10-5 = 48252 s = 13 h 24 min ( 2 demi-vie)

mouvement des planètes (4 points) La troisième loi de kepler a pour énoncé : " le carré de la période de révolution T de chaque planète est proportionnel au cube du demi grand axe, noté a, de son orbite elliptique " Donner le référentiel utilisé pour étudier le mouvement des planètes. - Traduire par une relation mathématique l'énoncé de la 3ème loi de Kepler. Planète Pluton Terre Jupiter Saturne demi grand axe a 39,3 1 5,203 ? période de révolution T ? 1 ? 29,45 - Donner l'unité de période utilisée dans ce tableau. - L'unité de distance utilisée est l'unité astronomique u.a. Expliquer ce qu'elle représente ? - Compléter le tableau précédent. Classer ces 4 planètes par ordre d'éloignement croissant au soleil. La constante intervenant dans la 3ème loi de Kepler est 4p2 / (GMS) où MS est la masse du soleil. - Montrer que cette constante s'exprime en s2m-3. - En déduire la masse du soleil. G= 6,67 10-11 S.I ; 1 u.a = 150 millions de km. corrigé référentiel héliocentrique ( origine : centre du soleil et les trois axes pointent vers des étoiles lointaines qui paraissent fixes) 3ème loi de Kepler : T² / a3 = constante T : période de révolution et a : demi-grand axe de l'ellipse. unité de période : la période terrestre 365,25 jours 1 u.a : distance terre-soleil = 1,5 1011 m. avec ces unités le rapport T² / a3 = 1 TP² / aP3 = 1 soit TP²=aP3 = 39,33 = 60698 ; TP= 246,4. TJ² / aJ3 = 1 soit TJ²=aJ3 = 5,2033 = 140,85 ; TJ= 11,87. TS² / aS3 = 1 soit aS3 = TS²= 29,452 = 867,3 ; aS= 9,54. Terre < Jupiter < Saturn < Pluton (la plus éloignée du soleil) 4p² est sans dimension ; MS : masse en kg. G, constante de gravitation : force * distance ² / masse ² force = masse *accélération = masse * distance* temps -2. G : distance3 * masse -1 * temps -2 ; 4p² / (GMS) : distance-3 * temps 2 soit m-3 s2. TTerre² / aTerre3 = 365,25*24*3600 / (1,5 1011)3 =2,95 10-19. 2,95 10-19=4p² / (GMS) d'où MS= 4p² / (G*2,95 10-19) = 4*3,14² / (6,67 10-11*2,95 10-19) = 2 1030 kg.

retour - menu