concours kiné Limoges 03 sans calculatrice

radioactivité (5 points) Le radium 226 se transforme en radon 222 par une émission radioactive notée E1. Le radon 222 se transforme en polonium 218 dont le nombre de charge vaut 82 par une émission radioactive notée E2. noyau nombre de noyaux présents à la date t activité à la date t constante radioactive demi-vie masse d'un noyau en u 22686Ra N1 A1 l1 t½(1) =1600 ans 225,9771 22284Rn N2 A2 l2 t½(2) =3,65 jours 221,9704 42He 4,0015 On prendra 1 u = 900 MeV/c² ; ln 2 = 0,7. On pourra utiliser l'approximation ex = 1+ x quand x est voisin de zéro. Ecrire les équations des désintégrations radioactives E1 et E2. On dira leur type. - Calculer l'énergie libérée dans l'émission E1. Comment se manifeste cette énergie ? - Calculer l2 /l1 . Quelle constante peut-on négliger devant l'autre ? - Quelle est la variation relative d'activité du radium en 1,6 an ? Quelle conclusion peut-on en tirer ? Des calculs théoriques montre que l'activité du radon est donnée par : A2 = N0 l2 l1 / (l2 -l1) e-l1 t (1-e(l1 -l2)t). N0 est le nombre de noyaux de radium présents à la date t=0. Compte tenu des résultats obtenus en 1- montrer qu'au bout d'un temps suffisant les activités du radium et du radon sont égales. On dit que l'on a un équilibre séculaire. - La masse de radium initiale est de 1,6 g. Cette masse, tout comme l'activité du radium seront considérée constantes sur l'intervalle de temps étudié. En considérant les masses des noyaux de radium et de radon égales, déduire la masse de radon en équilibre séculaire avec la masse de radium. corrigé 22686Ra --> 22284Rn+ 42He émission a. 22284Rn --> 21882Po+ 42He émission a. variation de masse |Dm|=225,9771-(221,9704+4,0015)=5,2 10-3 u. énergie libérée : E= 5,2 10-3 *900 = 4,68 MeV. La particule a emporte l'essentielle de cette énergie sous forme d'énergie cinétique. l1 t½(1) = ln2 ; l2 t½(2) = ln2 ; l2 /l1 = t½(1) / t½(2) = 1600*365/3,5 = 1,6 105. l1 négligeable devant l2 . A1= A0 e-l1t ; A1/ A0 =e-l1t ; 1-A1/ A0 = 1-e-l1t ; r = (A0 -A1)/ A0 =1-e-l1t voisin de 1-(1- l1t)) soit l1t si l1t est petit r = (A0 -A1)/ A0 proche de ln2 / t½(1) * t = 0,7/1600*1,6 = 7 10-4. l'activité est pratiquement inchangée à t = 1,6 ans. A1= l1 N0 e-l1t ; A2 = N0 l2 l1 / (l2 -l1) e-l1 t (1-e(l1 -l2)t) = A1l2/ (l2 -l1) (1-e(l1 -l2)t) or l1 <<l2 d'où l2 -l1 proche de l2 et A1 = constante si t<1,6 ans. A2voisin de A1(1-e(-l2t)) si l2 t est grand ( t>40 jours) alors (1-e(-l2t)) proche de 1 et A2voisin de A1 masse molaire du radium voisine de masse molaire du radon, notée M. A1 = N1 l1 proche de N0 l1avec N0 = 1,6 / M*6,02 1023 noyaux A2 = N2 l2 proche de A1 avec N2 = m / M*6,02 1023 noyaux N2 /N0 = l1 / l2 = m/1,6 ; m= 1,6 l1 / l2 = 1,6 / 1,3 105 = 10-5 g.

glissement sur une table On considère deux solide s et S' de masses respectives M et M', reliés par un fil inextensible et sans masse; la poulie est supposée sans frottement et de masse négligeable. A l'instant t=0 le système est immobile. S' chute d'une hauteur h sur le sol ; S glisse sur le support horizontal d'une distance d. S et son support n'étant pas parfaitement lisses, il existe lors du glissement de S sur son support, une force de frottement solide f et l'on fait l'hypothèse que la valeur de f est constante. 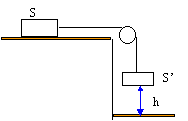A partir du bilan des forces extérieires appliquées sur S', appliquer le th. de l'énergie cinétique au mouvement de S' entre la date t=0 et la date t1 à laquelle il pecute le support. A la date t1 la vitesse atteinte par S sera notée v. A partir du bilan des forces exercée sur S, appliquer le th. de l'énergie cinétique aux deux phases du mouvement de S : - entre la date t=0 et t1 ; - entre la date t1 et la date t2 à laquelle la vitesse s'annule ; la distance totale parcourue entre t=0 et t2 est appelé d. En déduire l'expression de la force de frottement en fonction de M, M', d, h et g. 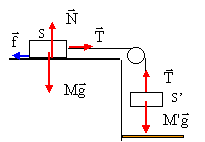corrigé ½M'v²-0 = travail du poids + travail de la tension ½M'v²-0 = M'gh-Th (1) phase (1) : T différente de zéro ; le poids et l'action du plan sont perpendiculaires à la vitesse et en conséquence ne travaillent pas. M et M' ont la même accélération, donc la même vitesse. ½Mv² -0 = travail de la tension + travail des frottements ½Mv² = T h - f h (2) phase (2) : T nulle ( fil non tendu) ; 0-½Mv² = -f (d-h) (3) (2) et (3) donnent : T h - f h = f (d-h) soit T h = f d.(4) (3) donne v² = 2 f(d-h)/M repport dans (1) : ½M' 2 f(d-h)/M = M'gh- f d M'f(d-h)/M + f d = M'gh f [M'(d-h)/M+d]=M'gh soit f = M' M g h / [ M'(d-h) +M d] . dans

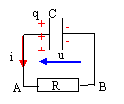
circuit RC   Un condensateur de capacité C= 50 mF, préalablement chargé sous une tension E=20 V est connecté à un conducteur ohmique de résistance R= 100 W. Etablir l'équation différentielle faisant intervenir la quantité d'électricité instantanée q(t) présente sur l'armature A du condensateur au cours de la décharge. - q(t) = Q0 e-t/t est la solution. En déduire l'expression de la constante t. Déterminer l'expression de la constante Q0. Donner l'expression de l'intensité i(t) et établir l'expression de la tension instantanée u(t) en fonction de E, R, C et t. On considère le condensateur complétement déchargé lorsque q=Q0 / 100, Q0 étant la charge initiale à t=0. Quelle valeur R' de la résistance faut-il utiliser pour que la décharge s'effectue en 1 s ? On donne ln 100 = 4,6 et ln 0,01 = 0,22. Calculer l'énergie initiale W0 emmagasinée dans le condensateur. déterminer l'expression de l'énergie perdue par effet joule dans le conducteur ohmique de résistance R= 100 W au cours de la décharge, jusqu'à la décharge totale. Conclure.     corrigé uAB=Ri ; uAB= q/C et i = -dq/dt = -q' ( décharge) Ri=q/C soit R(-q') =q/C ou encore q' +1/(RC) q=0 avec t = 1/(RC) ( constante de temps) Q0 , charge initiale ; Q0 = CE = 50 10-6*20 = 10-3C. i = -dq/dt et q= Q0 e-t/t soit i = -Q0 (-1/t ) e-t/t = Q0 /t e-t/t . i = Q0 /(RC) e-t/t = CE/(RC) e-t/t =E/R e-t/t . u = q/C = CE/C e-t/t =E e-t/t . Q0/100=Q0 e-t/t soit 0,01 =e-1/t ; ln 0,01 = -1/t ; ln 100 = 1/t soit t =1 / 4,6 R'C = 1/4,6 soit R' = 1/(4,6 * 50 10-6 ) = 105 / (4,6*5 )= 4350 W. W0 = ½CE² = 0,5*50 10-6*20² = 0,01 J. W0 = Wjoule.

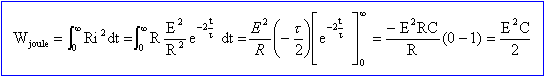
tir de balles dans l'eau d'une piscine Un fusil spécial peut envoyer des balles, type balles de tennis, de masse m=100g, à la vitesse v0=24 m/s. On tire verticalement vers le bas vers l'eau d'une piscine profonde. On supposera que la balle pénètre dans l'eau à l'instant t =0 avec la vitesse v0. Dans l'eau la balle subit une force de frottement proportionnelle à la vitesse, le coefficient de proportionnalité étant h= 0,25 SI. Un volume d'eau égal à celui de la balle aurait une masse m' = 250 g. On prendra g=10 m/s². On ne considèrera que le mouvement de la balle dans l'eau, l'axe Oz est vertical vers le bas. A quelle force la balle est-elle soumise une fois dans l'eau ? Faire un schéma - Etablir l'équation différentielle à laquelle obéit la vitesse v. La solution de cette équation différentielle est : v=v0 e-h/mt + g(m-m') / h ( 1-e-h/mt ) - Donner l'expression de la vitesse limite vl dans l'eau. Faire l'application numérique. Si cette vitesse limite est atteinte vers où se dirige la balle ? - Calculer le temps t caractéristique du mouvement. - Au bout de combien de temps aptrès avoir pénétré dans l'eau la balle se met-elle à remonter ? On prendra ln0,2 =-1,6. 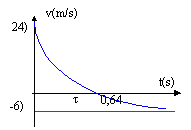- A l'aide des résultats précédents donner l'allure de la courbe représentant la vitesse en fonction du temps. 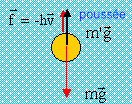corrigé poids, verticale vers le bas, mg = 0,1*10 = 1N poussée d'Archimède, verticale, vers le haut ( poids du volume de liquide déplacé ) , m'g frottement, verticale, sens opposée à celui de la vitesse , valeur 0,25 v la seconde loi de Newton s'écrit, projetée sur un axe verticale orienté vers le bas ( descente de la balle) mg-m'g-0,25 v = ma = m dv/dt mdv/dt + 0,25 v = g(m-m'). au bout d'un temps suffisamment long la vitesse limite est atteinte et e-h/mt tend vers zéro. v=v0 e-h/mt + g(m-m') / h ( 1-e-h/mt ) donne : vlim = g(m-m')/h = 10(0,1-0,25) / 0,25 = -6 m/s. le signe moins traduit le fait que la vitesse limite est orientée en sens contraire de l'axe précédent : donc la balle remonte. constante de temps t = -m/h = -0,1/0,25 = 0,4 s. La vitesse est nulle à l'instant où la balle commence à remonter. 0 =v0 e-h/mt + vlim ( 1-e-h/mt )  0 =v0 e-h/mt + vlim -vlim e-h/mt . e-h/mt (vlim -v0 ) = vlim . -ht/m = ln[ vlim / (vlim -v0 ) ] soit t = t ln[(vlim -v0 ) / vlim ] t = 0,4 ln[(-6-24)/ (-6)]=0,4 ln5 = 0,64 s.

acide base   exercice 1 : On dispose des couples acide/base: acide éthanoïque / ion éthanoate pKa = 4,8 ; acide méthanoïque / ion méthanoate pKa = 3,8. On donne pKe = 14. A partir de solutions demême concentrations c=0,1 mol/L on prépare les solutions S1, S2, S3, S4 : ac méthanoïque méthanoate de sodium ac éthanoïque éthanoate de sodium pH S1 10 mL 20 mL 4 S2 25 mL 5 mL 4,1 S3 1 mL 10 mL 4,8 S4 10 mL 1 mL 3,8 On mélange ensuite les solutions S1 et S2 conduisant à une solution M et le solutions S3 et S4 conduisant à une solution M'. Montrer à partir du calcul du taux d'avancement, que pour la solution S1, tout se passe comme si les entités acido-basiques introduites en solution n'avaient pas réagi avec l'eau. Un calcul analogue montre que l'eau ne réagit pas avec les entités acido-basiques apportées par les solutions S2, S3, S4 . Ecrire l'équation de la réaction acido-basique modélisant la transformation susceptible de se produire dans le mélange M et le mélange M'. Exprimer la constante d'équilibre et calculer sa valeur. Déterminer dans quel sens se produit la transformation dans le mélange M et dans le mélange M'. exercice 2 : le calcaire et le tartre contiennent essentiellement du carbonate de calcium CaCO3. Ce composé est peu soluble dans l'eau pure. Cette dissolution se fait selon l'équation : CaCO3 = Ca2+ + CO32-. Dans une eau calcaire chargée en dioxyde de carbone, il se passe une réaction dont la constante d'équilibre vaut K= 103,9 ; l'équation de cette réaction est : CO32-+ CO2 + H2O = 2HCO3- (1) On donne les couples acide/base suivants avec leur constante d'acidité : HCO3-/CO32- ; Ka1 = 10-10,3 ; CO2 + H2O /HCO3- ; Ka2 = 10-6,4 ; montrer comment on peut retrouver la constante K à partir des constantes d'acidité. Des facteurs physiques et physico-chimiques influent sur l'évolution de la réaction (1). On demande comment évolue le système {CO32- ; HCO3- } : - si l'eau subit un apport de sources volcaniques riches en CO2 dissout. - si la température de l'eau s'élève. - si les plantes prélèvent CO2 par synthèse chlorophyllienne corrigé HCOOH +H2O =HCOO- +H3O+ initial 0,01*0,1 = 10-3 mol 2 10-3 mol en cours 10-3 -x 2 10-3 +x x final 10-3 -xmax=0 xmax= 10-3 mol 2 10-3 +xmax xmax= 10-3 mol or xfin = [H3O+]* volume (L) = 10-pH*0,03 = 10-4*0,03 = 3 10-6 mol. taux d'avancement final = t = xfin / xmax = 3 10-6 / 10-3 = 3 10-3. valeur très inférieure à 1 donc les entités présentes initialement réagissent très peu avec l'eau. dans M ou dans M' : HCOOH +CH3-COO- =HCOO- + CH3-COOH K = [HCOO- ][CH3-COOH]/([HCOOH][CH3-COO-]) K = [HCOO- ] [H3O+]/[HCOOH] *[CH3-COOH] / ( [CH3-COO-] [H3O+])= 10-3,8 / 10-4,8 = 10. dans M : [HCOO- ]i= 0,02*0,1 / (( 20+10+25+5)10-3) = 2/60 mol/L ; [HCOOH]i= 0,01*0,1 / (( 20+10+25+5)10-3) = 1/60 mol/L ; [CH3-COOH]i= 0,025*0,1/(60 10-3 ) = 2,5/60 mol/L [CH3-COO- ]i= 0,05*0,1/(60 10-3 ) = 0,5/60 mol/L Qr,i = 2*2,5 / (1*0,5) = 10 le quotient initial est égal à la constante d'équilibre K donc on se trouve à l'équilibre chimique et la composition du mélange ne change pas. dans M' un calcul analogue donne Qr,i = 100. le quotient initial est supérieur à la constante d'équilibre K donc le système évolue en sens indirect, de la droite vers la gauche. K= [HCO3- ][HCO3- ]/([CO2][CO32-]) Ka1= [CO32-] [H3O+] / [HCO3- ] donne [HCO3- ] / [CO32-] = [H3O+] / Ka1. Ka2= [HCO3- ][H3O+] / [CO2] donne [HCO3- ] / [CO2] = Ka2/[H3O+]. d'où K= Ka2/Ka1= 10-6,4 / 10-10,3 = 103,9. si apport de CO2 , déplacement dans le sens direct, consommation de CO2. si la température s'élève , K augmente et déplacement dans le sens direct. si on prélève CO2 , déplacement dans le sens indirect, formation CO2 .

pile   On réalise une pile qui met en oeuvre les couples oxydo-réducteurs Al3+ / Al et Fe2+/ Fe. Les électrodes sont placées dans des solutions de volumes 60 mL où les concentrations des ions métalliques valent toutes deux 0,5 mol/L. On donne la constante d'équilibre pour la réaction entre les ions Fe2+ et Al : K= 10122. En utilisant le critère d'évolution spontanée : - On indiquera l'équation de la transformation qui se produit dans cette pile. - On fera le schéma conventionnel de cette pile. Sur chaque électrode indiquer la réaction qui se passe en précisant s'il s'agit de l'anode ou de la cathode. Faire un tableau d'avancement de la transformation. Les plaques métalliques sont toujours présentes . L'instant final sera celui où les ions consommables auront tous été consommés. - Quelle masse minimale de métal faut-il pour arriver à l'instant final ? ( masse molaire atomique Fe =56 et Al=27 g/mol) - Dans l'hypothèse précédente, pendant combien de temps la pile peut-elle débiter une intensité constante de 60 mA ? 1 faraday = 96500 C corrigé 3 Fe2+ + 2 Al = 2Al3+ + 3Fe ; K= [Al3+]2 /[Fe2+]3. Qr,i = [Al3+]i2 /[Fe2+]i3 = 0,52 / 0,53 = 1/0,5 = 2. Qr,i < K donc évolution dans le sens direct, de gauche à droite. Fe2+ + 2e- = Fe, réduction à la cathode Al = Al3+ +3e- , oxydation à l'anode négative. - Al / Al3+ // Fe2+ / Fe +. 3 Fe2+ + 2 Al = 2Al3+ + 3Fe t=0 0,5*0,06 = 0,03 mol n1 (excès) 0,03 mol n2 (excès) en cours 0,03-3x n1-2x 0,03+2x n2 + 3x fin (pile usée) 0,03-3xmax=0 n1-2xmax= 0 0,03-3xmax=0 soit xmax=0,01 mol n1-2xmax = 0 soit n1 = 0,02 mol ou 0,02*27 = 0,54 g. Qté d'électricité Q(C) = I(A) * t(s) = 0,06 t autre manière de calculer Q : Fe2+ + 2e- = Fe 0,01 mol d'ion Fe2+ et en conséquence 2*0,01 = 0,02 mol d'électrons. la charge d'une mole d'électrons est 1 F ou 96500 coulombs Q = 0,02*96500 = 1930 C et t = 1930 / 0,06 = 32166 s. retour - menu