|
|
|
|
|
|
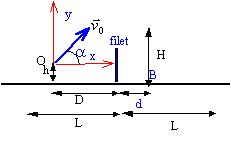
Un joueur de tennis est situé en A à la distance D=9m du filet et tente de lober son adversaire situé en B à une distance d=2 m du filet. Le joueur frappe la balle à une hauteur h=0,5 m du sol avec un angle de tir a=60° et une vitesse v0 =43,2 km/h. On assimile la balle à un point matériel de masse m=60g. g=10 m/s² ; les frottements sont négligés.
- Calculer l'énergie cinétique (J) de la
balle au moment où elle quitte la raquette.
56 ; 0,36 ; 43,2 ; 360 ; 4320 ; 3,6 ; 4,32 ; 5,6. - Quelles sont les affirmtions suivantes qui sont
vraies ?
a- La balle de tennis a un mouvement de chute libre.
b- Le vecteur accélération du centre d'inertie de la balle est égal au poids de la balle.
c- Le mouvement de la projection du centre d'inertie de la balle suivant l'axe horizontal Ox est uniformément varié.
a seule ; b seule ; c seule ; a t b ; a et c ; b et c ; toutes ; aucune. - Calculer l'altitude maximale (m) de la balle par
rapport au sol.
7 ; 5,4 ; 12 ; 5 ; 11,5 ; 11 ; 6,4 ; 5,9. - Combien de temps (s) met la balle pour atteindre la
hauteur maximale ?
1,4 ; 1,2 ; 0,64 ; 2,06 ; 1,04 ; 2,24 ; 0,26 ; 1,64. - Calculer l'altitude (m) de la balle par rapport au
sol lorsqu'elle passe juste au dessus du joueur B ?
2,07 ; 2,75 ; 3,07 ; 1,75 ; 3,75 ; 0,75 ; 1,07 ; 7,05 - Calculer la distance (m) parcourue par la balle
jusqu'au premier point d'impact au sol.
12,05 ; 12,75 ; 11,57 ; 22,75 ; 5,75 ; 6,57 ; 24,75 ; 26,85. - Sachant que la longueur totale du terrain est 24 m et
que le joueur est capable d'intercepter au maximum une
balle qui passe au dessus de lui à une hauteur de
2,8m, quelles sont les affirmations suivantes qui sont
fausses ?
a- La balle a touché le sol pour la première fois 2m derrière le joueur B.
b- Si la masse de la balle double, dans les mêmes conditions le lob aurait été raté.
c- Le travail du poids de la balle de tennis entre le point O et le premier point d'impact au sol vaut 2,94 J
a seule ; b seule ; c seule ; a et b ; a et c ; b et c ; toutes; aucune
corrigé
énergie cinétique de la balle : Ec= ½mv0²
m= 0,06 kg ; v0 = 43,2/3,6 =12 m/s : Ec=0,5*0,06*12² = 4,32 J.
2a- vrai ;
2b- : faux ; une accélération n'est pas égale à un poids ;
2c- : faux ; suivant l'axe horizontal, le mouvement est uniforme ; la composante verticale de la vitesse varie mais pas sa composante horizontale ( la vitesse ne varie que dans la direction de la force, le poids)
altitude maximale :
appliquer le théorème de l'énergie cinétique entre le sommet de la trajectoire et le point de départ :
travail du poids: -mg(hmaxi-h)
½mv²fin -½mv²0 = -mg(hmaxi-h)
v²fin -v²0 = -2g(hmaxi-h) soit hmaxi-h= (v²fin -v²0 ) / (-2g)
à l'altitude maximale, le vecteur vitesse est horizontal, sa valeur est v0cosa = 12 cos60 =6 m/s
hmaxi-h=( 36-144) / (-20) = 5,51 m e thmaxi= 5,4 + 0,5 = 5,9 m.
durée pour atteindre hmaxi :
composante verticale de la vitesse v = -gt + v0
0 = -gtmaxi + v0 soit : tmaxi = v0 /g = 12 / 10 = 1,2 s.
altitude de la balle au dessus de B :
y = -½gt² + v0 sin a t ; x =v0cosa t
trajectoire : y = -½gx² / (v0cosa)² + x tana = -0,1389 x² +1,732 x
xB = D+d = 11 m ; yB= -0,1389 *11² + 1,732*11 = 2,25 m soit 2,75 m par rapport au sol
distance jusqu'au point d'impact au sol :
au sol y = -0,5 ; -0,5 =-0,1389 x² +1,732 x ;-0,139 x² +1,732 x + 0,5=0
x² - 12,47 x- 3,6 =0 ; D = 12,47²+4*3,6 =169,9 ; x = 12,75 m.
La balle passe à 2,75 m au dessus de B: il est capable de l'intercepter
sinon la balle tombera 12,75-D= 12,75 -9 = 3,75 m à droite du filet. (1,75 m derrière B)
7a- : fausse ; 7b- : fausse : la masse n'intervient pas dans l'expression de la trajectoire
le travail du poids ne dépend que de la différence d'altitude entre le départ et l'arrivée soit 0,5 m :
mgh = 0,06*10*0,5 = 0,3 J donc 7c- : fausse.
Pour déterminer la constante de raideur k d'un ressort à spires non jointives de masse négligeable, on accroche unede ses extrémité à un support fixe et à l'autre extrémité une masse m=200g. Le ressort s'allonge de 10 cm. g=10 m/s²; on néglige les frottements.
- Calculer la constante de raideur (N/m) de ce
ressort.
20 ; 200 ; 0,2 ; 2 ; 0,5 ; 0,005 ; 5 ; 0,05. - On fixe le ressort précédent
horizontalement. L'une de ces extrémité A
est fixe ; on accroche à l'autre
extrémité un solide S de masse m=200g. Ce
solide peut se déplacer sans frottement le long
d'un axe horizontal Ox. A l'équilibre le centre de
gravité du solide S coïncide avec l'origine O
du repère. A un instant t on écarte le
solide de sa position d'équilibre et on le
lâche sans vitesse initiale. Quelles sont les
affirmations suivantes qui sont fausses ?
a- La force exercée par le ressort sur le solide S est une force dite force de rappel.
b- Quand le solide repasse par la position d'équilibre la vitesse est minimale.
c- La solution de l'équation différentielle du mouvement du solide est de la forma x(t) = Xmax cos ((k/m)½ t+j)
a seule ; b seule ; c seule ; a et b ; a et c ; b et c ; toutes; aucune - Calculer la fréquence (Hz) propre de cet
oscillateur .
63,83 ; 0,159 ; 0,628 ; 0,0628 ; 1,59 ; 6,28 ; 0,0159 ; 15,91. - On comprime maintenant le ressort en poussant le
solide vers la gauche. Le point G occupe la position
G0 telle que l'abscisse de G0 soit
-0,15 m. A l'instant t on lâche le ressort sans
vitesse initiale. Calculer la vitesse maximale
vG (m/s)du solide.
1 ; 0,15 ; 3 ; 2 ; 2,5 ; 3,5 ; 1,5 ; 0,5. - Calculer l'énergie mécanique (mJ) de
cet oscillateur.
1500 ; 450 ; 300 ; 225 ; 500 ; 600 ; 150 ; 475.
corrigé
raideur k = mg/ allongement = 0,2*10 / 0,1 =20 N/m.
a : vraie ; b : fausse ( au passage à la position initiale, la position d'équilibre, la vitesse est maximale) ; c : vraie.
fréquence :
w0 = rac carrée (k/m) = (20/0,2)½ = 10 rad/s.
f0 = w0 / (2*3,14) = 10/6,28 = 1,59 Hz.
vitesse maxi vG :
au départ l'énergie est sous forme potentielle élastique : ½kx²
au passge à la position d'équilibre l'énergie est sous forme cinétique :½mv²
conservation de l'énergie mécanique : ½kx² = ½mv²
v² = k/ m x² = 20/0,2 * (-0,15)² = 2,25 ; v= 1,5 m/s.
énergie mécanique : ½kx² = 0,5*20 *(-0,15)² =0,225 J = 225 mJ.
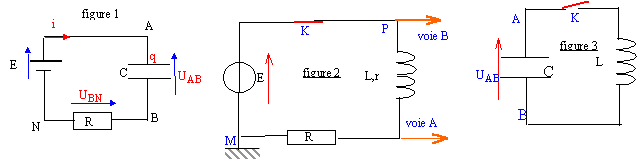
Un condensateur de capacité C= 1mF, initialement déchargé, placé en série avec un conducteur ohmique R= 10kW est chargé par un générateur parfait de fem E= 5V. A l'instant t=0 on ferme le circuit (figure 1).
- Quelles sont les affirmations suivantes qui sont
vraies ?
a- le milieu qui se trouve entre les deux armatures d'un condensateur est un isolant.
b- La tension aux bornes du condensateur est d'autant plus petite que la valeur absolue de la charge portée par ses armatures est grande.
c- L'équation différentielle de la charge du condensateur admet cette expression : Rdq/dt + q /C =E
a seule ; b seule ; c seule ; a et b ; a et c ; b et c ; toutes; aucune - Calculer le temps nécessaire (ms) pour que le
condensateur se charge à 63% de sa valeur
maximale
10000 ; 1 ; 0,01 ; 100 ; 1000 ; 10 ; 0,1 ; 0,001 - Calculer l'énergie maximale
emmagasinnée par le condensateur.
12,5 mJ ; 12,5 mJ ; 25 mJ ; 25 mJ ; 12,5 J ; 2,5 mJ ; ; 1,25 mJ ; 25 J
On réalise le circuit de la figure 2 ci-dessus. E=10 V ; R=270 ohms. Un oscilloscope à mémoire permet d'enregistrer les tensions.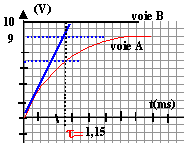
- Quelles sont les affirmations suivantes sui sont
fausses ?
a- Une bobine s'oppose aux variations d'une tension dans un circuit.
b- L'amplitude de la tension imposée aux bornes du dipôle RL n'a aucune influence sur la constante de temps du circuit.
c- La tension visualisée voie A sur l'oscilloscope est la tension aux bornes de la bobine résistive.
a seule ; b seule ; c seule ; a et b ; a et c ; b et c ; toutes; aucune - Calculer l'intensité (mA) du courant qui
circule dans le circuit en régime permanent
30 ; 37 ; 3,7 ; 3 ; 27 ; 3,33 ; 33,3 ; 2,7 - Calculer la résistance r (ohm) de la
bobine
1 ; 10 ; 3 ; 13 ; 27 ; 30 ; 17 ; 20 - Après avoir lu t
sur le graphe, déterminer l'inductance L(H) de la
bobine.
435 ; 345 ; 405 ; 30 ; 534 ; 275 ; 445 ; 37,5.
On associe maintenant le condensateur chargé de capacité C=1mF en série avec la bobine d'inductance L et de résistance interne que l'on suppose négligeable.( figure3) A l'instant t on ferme l'interrupteur K et on enregistre la courbe donnant la tension uAB aux bornes du condensateur. Quelles sont les affirmations qui sont vraies ?
a- La courbe obtenue représente les oscillations sinusoïdales périodiques de la tension uAB.
b- Si la capacité du condensateur quadruple, la période des oscillations double.
c- Si l'on ajoute en série dans le circuit un conducteur ohmique de très grande résistance, on observera un régime apériodique.
a seule ; b seule ; c seule ; a et b ; a et c ; b et c ; toutes; aucune
corrigé
a : vrai ; b : faux ( tension et charge sont proportionnelles ) ; c : vrai
constante de temps t =RC = 104*10-6= 0,01 s = 10 ms.
énergie maximale stockée : ½CE² = 0,5*10-6*5² = 12,5 10-6 J = 12,5 mJ.
a : fausse (la bobine inductive s'oppose aux variations de l'intensité) ;
b : vraie ( la constante de temps est L/R) ; c : faux ( tension aux borne du résistor)
intensité en régime permanent :
en régime permanent la tension aux bornes du résistor vaut 9 V ( lecture graphe)
i = 9/R = 9/270 = 3,33 10-2 A = 33,3 mA.
en régime permanent la tension aux bornes de la bobine vaut 1 V ( lecture graphe)
1 = r*3,33 10-2 soit r = 100/3,33 = 30 ohms.
constante de temps t = L(R+r ) = 1,15 10-3 s
L = 1,15 10-3 * (270+30) = 0,345 H = 345 mH.
a : vrai ( pas d'amortissement car résistance nulle)
b : vrai ( période = 2p (LC)½ : si C quadruple ; L ne change pas alors la période double)
c : vrai.
Lacide benzoïque
C6H5COOH est un solide blanc à
25°C; sa solubilité est égale à
0,02 mol/L et son pKa = 4,2. On donne C=12, H=1, O=16 g/mol.
La solubilité est la quantité maximale d'acide
que l'on peut dissoudre dans un litre d'eau.
- Parmi les affirmations suivantes lesquelles sont
fausses ?
a- Lorsqu'on acidifie suffisamment une solution de benzoate de sodium C6H5COO- Na+ il se forme un solide blanc.
b- L'acide éthanoïque de pKa = 4,8 est un acide plus fort que l'acide benzoïque.
c- Si le pH d'une solution aqueuse contenant entre autre de l'acide benzoïque est égale à 5 , l'espèce majoritaire est l'acide benzoïque.
a seule ; b seule ; c seule ; a et b ; a et c ; b et c ; toutes; aucune - Calculer la masse d'acide benzoïque que l'on
peut dissoudre sans 100 mL d'eau pure.
2,44 g ; 24,2 mg ; 244 mg ; 2,44 mg ; 24,4 g ; 0,244 mg ; 0 g ; 244 g - On ajoute une solution d'hydroxyde de sodium à
0,1 mol/L à 75 mL d'une solution saturée
d'acide benzoïque additionnée de quelques
gouttes de phénolphtaléine. Pour quel
volume (mL) de la base versé le virage de
l'indicateur se produit-il ?
1 ; 10 ; 15 ; 5 ; 20 ; 25 ; 8 ; 12 - On mélange maintenant 10 mL d'acide
benzoïque à 0,001 mol/L et 5 mL d'une
solution d'éthylamine
C2H5NH2 à 0,001
mol/L. On donne
pKa(C2H5NH3+
/ C2H5NH2) =10,4.
Calculer la constante d'équilibre de la
réaction acido-basique.
3,16 107 ; 3,16 10-7; 3,16 10-6; 5,01 10-4; 3,16 106; 3,16 10-7; 1,58 10-4; 2000 ; 5 1010. - Sachant que la réaction entre l'acide
benzoïque et l'éthylamine est totale calculer
la concentration du benzoate d'éthylamonium (mmo /
L)
0,55 ; 1 ; 0,15 ; 3,3 ; 0,2 ; 0,33 ; 0,23 ; 0,66.
corrigé
a : vrai ( en acidifiant suffisamment la solution de benzoate de sodium, l'acide conjugué de l'ion benzoate, l'acide benzoïque prédomine : or ce dernier est très peu soluble dans l'eau)
b : faux ( à concentration égale, l'acide le plus fort possède le plus petit pKa)
c : faux ( à pH supérieur à pKa, c'est la forme base , ion benzoate qui est majoritaire)
masse d'acide benzoïque :
masse molaire de cet acide : 122 g/mol
solubilité à 25°C : 122*0,02 = 2,44 g/L soit 0,244 g (244 mg) dans 100 mL d'eau pure.
soude + acide benzoïque :
C6H5COOH + HO---> C6H5COO- +H2O
Quantité de matière d'acide : 0,075 * 0,02 = 1,5 10-3 mol
à l'équivalence la quantité de matière d'acide est égale à la quantité de matière de soude ajoutée
1,5 10-3 = 0,1 V soit V = 1,5 10-2 L = 15 mL.
C6H5COOH + C2H5NH2 = C2H5NH3+ +C6H5COO- .
K = [C2H5NH3+][C6H5COO-] /([C6H5COOH][C2H5NH2])
or C6H5COOH + H2O = C6H5COO- +H3O+ ;Ka1 = [C6H5COO-][H3O+]/[C6H5COOH]
et C2H5NH3+ + H2O = C2H5NH2 +H3O+ ;Ka2 = [C2H5NH2][H3O+]/[C2H5NH3+]
K = Ka1 / Ka2 =10-4,2 / 10-10,7 = 106,5 = 3,16 106.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[C6H5COO-]= 5 10-6 / ((10+5)10-3) = 3,33 10-4 mol/L= 0,333 mmol /L.
La stéarine est le triester de l'acide
stéarique( ou octadécanoïque) et du
glycérol (ou propan-1,2,3- triol). La formulke
semi-développée de l'acide stéarique
est CH3-(CH2)16-COOH.
C=12 ; O=16 ;H=1 ; Na=23 g/mol
- Calculer la masse molaire (g/mol) de la
stéarine.
874 ; 890 ; 902 ; 980 ; 889 ; 906 ; 878 ; 891. - On désire saponifier 178 g de stéarine
dans les conditions stoechiométriques par une
solution d'hydroxyde de sodium à 5 mol/L. Quel
volume (mL) de solution de soude doit-on utiliser ?
100 ; 300 ; 50 ; 240 ; 180 ; 120 ; 60 ; 150. - Sachant que la masse de savon obtenue
expérimentalement est137,7 g, calculer le
rendement (%)de cette réaction.
70 ; 80 ; 66 ; 100 ; 50 ; 33 ; 75 ; 65. - parmi les affirmations suivantes lesquelles sont
vraies ?
a- la fonction carboxylique de l'acide stéarique est hydrophobe.
b- l'acide stéarique est un acide gras.
c-la réaction de saponification est une réaction limitée.
a seule ; b seule ; c seule ; a et b ; a et c ; b et c ; toutes; aucune - La stéarine étant l'un des constituants
des bougies, calculer le volume (L) de dioxyde de carbone
fourni par la combustion totale de 1 g de stéarine
à 20°C sous une pression de 1 bar (volume
molaire 24 L/mol)
1,356 ; 1,753 ; 1,235 ; 1,836 ; 1,653 ; 1,153 ; 1,435 ; 1,537.
corrigé
masse molaire stéarine :
CH2-OOC-C17H35
|
CH-OOC-C17H35
|
CH2-OOC-C17H35
formule brute : C57 H110 O6 : 57*12+110+6*16 = 890 g/mol.
Qté de matière stéarine : 178 / 890 = 0,2 mol
C57 H110 O6+ 3(Na+ +HO-) --> CH2OH-CHOH-CH2OH (glycérol ) + 3(C17H35-COO- + Na+ )
soit 0,2*3 = 0,6 mol hydroxyde de sodium
volume soude = 0,6 / [soude] = 0,6 / 5 = 0,12 L = 120 mL.
rendement :
on peut espérer obtenir 0,6 mol de savon (C17H35-COO- + Na+ )
masse molaire stéarate de sodium (savon) : 18*12+35+32+23= 306 g/mol
masse de savon : 306*0,6 = 183,6 g
rendement : 137,7 *100 / 183,6 = 75 %.
a : faux ; le groupe -COOH, groupe polaire du fait de la présence des atomes d'oxygène est hydrophile.
b : exact ;
c: faux ( saponification lente mais totale)
C57 H110 O6+ (57 + 55/2-3)O2 --> 57 CO2 + 55 H2O
Quantité de matière stéarine 1/890 mol
Qté de matière dioxyde de carbone : 57/890 mol
volume dioxyde de carbone : 57*24 / 890 = 1,537 L.