concours kiné E.F.O.M 03 physique 1 h - 20 points- chimie ½ h- 10 points. sans calculatrice.

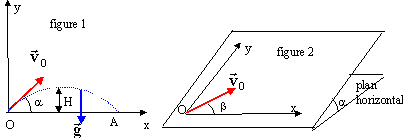
tirs paraboliques A- Un projectile est lancé dans le champ de pesanteur terrestre uniforme avec un vecteur vitesse v0 faisant un angle a avec l'horizontale passant par le point de lancement O. figure 1. Etablir l'équation de la trajectoire dans le repère (O,x,y). Exprimer en fonction de a, g et v0 la portée horizontale P=OA. Pour quelle valeur de a cette portée est-elle maximale ? Exprimer cette portée Pmax en fonction de v0 et g. Exprimer en fonction de a, g et v0 la fléche H, altitude du sommet de la parabole. Pour quelle valeur de a , H est-elle maximale ? Exprimer Hmax en fonction de v0 et g. On veut atteindre le point B de coordonnées (½Pmax ; ½Hmax), la vitesse v0 étant fixée. Montrerqu'il y a seux angles de tir a 1 et a 2 permettant d'atteindre ce point B. Proposer une méthode qualitative permettant de déterminer ces deux angles. Donnée : 1/cos²a = 1+tan²a B- Sur un plan incliné d'un angle a par rapport au plan horizontal, on lance un solide ponctuel, mobile sans frottement, avec une vitesse v0 (figure 2 ci-dessus). Etablir l'équation de la trajectoire dans le repère (O,x,y) en fonction de a, b, g et v0. Le solide revient sur l'axe Ox en un point O'. Donner l'expression de la distance OO' en fonction de a, b, g et v0. Soit H l'altitude maximale atteinte par le solide, comptée à partir du niveau de Ox. Montrer que H vérifie la relation H= v0² sin²b / (2g). 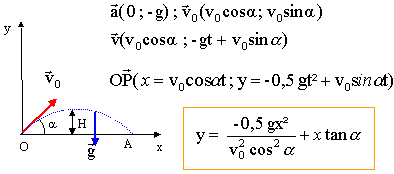corrigé portée : y=0 0= -½gx²/(v0²cos²a) + x sin a / cosa. x= 0 ( origine de l'axe) ; -½gx/(v0²cosa) + sin a =0 donne x = 2v0²cosa sin a /g =v0² sin (2a) /g la portée est maximale si : sin (2a) =1 soit a = p /4 ; Pmaxi =v0² /g. flèche : la tangente à la trajectoire est horizontale ; la composante verticale de la vitesse est donc nulle -gt +v0sina =0 soit t =v0sina /g repport dans y : H=-½ g(v0sina /g)² +v0sinav0sina /g =v0² sin ²a /(2g) la flèche est maximale si a = p /2 ( tir vertical) ; Hmaxi =v0² /(2g) atteindre B(v0² /(2g) ; v0² /(4g)) avec v0 constant. écrire que B est situé sur la trajectoire : v0² /(4g) =-½g [v0² /(2g)]² /(v0²cos²a) +[v0² /(2g)] tan a. 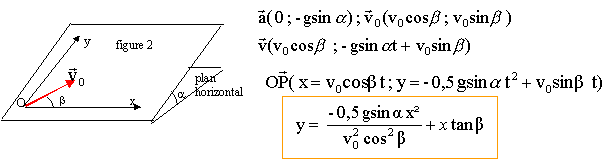1 = -½ 1/cos²a+ 2tan a ; 1 = -½[1+tan² a]+2tan a ; 1,5 +0,5 tan² a-2tan a =0 ou bien tan² a-4tan a + 3=0 on pose X=tan a et on résoud l'équation : X² -4X +3=0 X=3 soit tan a=3 et a = 71,56° ; X=1 soit tan a=1 et a = 45° ;  au point O' : y=0 0= -½gsin a x²/(v0²cos²b) + x sin b / cosb. x= 0 ; -½g sin a x/(v0²cos b) + sin b =0 donne x = 2v0²cosb sin b /(gsin a) =v0² sin (2b) /(gsin a) flèche : la tangente à la trajectoire est horizontale ; la composante verticale de la vitesse est donc nulle -gsinat +v0sinb =0 soit t =v0sinb /(gsina ) repport dans y : ymaxi= -½ g(v0sinb /(gsina ))² +(v0sinb )²/(gsina ) =v0² sin ²b /(2gsina)   H= ymaxisina = v0² sin ²b /(2g)

saut à l'élastique Le sauteur 'S) de masse m=100 kg sear assimilé à un point matériel. L'élastique utilisé est assimilé à un ressort parfaitement élastique de longueur à vide L0=50 m et de constante de raideur k. g=10m/s² et on néglige les frottements de l'air. Le sauteur est hissé en haut d'une grue à l'aide d'une nacelle, de masse M=200kg, qui joue le rôle d'un ascenceur. La nacelle s'élève jusqu'à un point O1. Faire le bilan des forces extérieures qui agissent sur le système {nacelle + sauteur} lors de la montée. - La nacelle démarre avec une accélération a1=1 m/s², puis s'élève à vitesse constante et ralentit avec une décélération a3 de valeur 1,2 m/s². Calculer la tension du câble supposée constante, qui maintient la nacelle contenant le sauteur durant les 3 étapes de cette ascension. Em position O1 la porte de la nacelle est ouverte, le sauteur quitte la nacelle sans vitesse initiale. Dans cette phase de saut le sauteur est en chute libre jusqu'au point O tel que O1O=L0. Ce point O est choisi comme origine de l'axe vertical descendant Ox. Puis l'élastique commence à se tendre ; son allongement est x=10 m lorsque le sauteur S atteint sa position la plus basse notée O2. - Ecrire l'expression de l'énergie mécanique du système {sauteur, élastique terre}. - En utilisant la conservation de l'énergie mécanique de ce système, déterminer la tension maximale de l'élastique au cours de ce saut. - Quelle masse m' faudrait-il suspendre au même élastique, à l'équilibre statique, pour obtenir la même tension. - Donner l'expression de la vitesse maximale du sauteur en fonction des données du problème. Le sauteur atteint le point O2 puis remonte jusqu'à un point O'2 avec un mouvement correspondant à des oscillations libres, non amorties et parfaitement sinusoïdales. - Donner l'expression de l'équation horaire x(t) de ce mouvement. - Préciser les expressions de l'amplitude, la période propre et la vitesse maximale de ce mouvement oscillatoire.   corrigé poids (nacelle + sauteur) vertical vers le bas (M+m)g = 300 *10 = 3000 N. tension du câble, verticale vers le haut La 2ème loi de newton s'écrit, en projection sur un axe vertical, vers le haut : T-(M+m)g =(M+m)a soit T = (M+m) (g+a) T1 = 300*(10+1) = 3300 N T2 = 300*(10+0) = 3000 N T3 = 300*(10-1,2) = 2740 N ( a3 sens contraire de l'axe car décélération) E mécanique = E cinétique + E potentielle de pesanteur + E potentielle élastique. E = ½ mv² + mgh + ½k(L-L0)² L'origine des altitudes est choisie au point le plus bas. en O1 ( départ) l'énergie mécanique est sous forme potentielle de pesanteur : E = mg(L0+X) = 1000*60 = 60000 J. en O, l'énergie mécanique ( élastique non tendu) : E = ½ mv² + mgX en O2 ( point le plus bas) l'énergie mécanique est sous forme potentielle élastique : E = ½k(L-L0)² = 0,5 k(60-50)² = 60000 ; 50k = 60000 soit k = 1200 N/m. tension maximale en O2 : T m= kX = 1200*10 = 12 000 N. à l'équilibre statique, poids et tension sont opposées ( ont même valeur) m' g = T m= kX soit m' = 12000 / 10 = 1200 kg. La vitesse est maximale si l'énergie mécanique est entièrement sous forme cinétique : E = ½mv²max = mg(L0+X) ; v²max = 2g(L0+X) l'amplitude du mouvement oscillatoire non amorti est X=10 m. x(t) = X cos (w0t+j) avec w0² = k/m =1200/100 =12 soit w0 =3,46 rad/s. période T0 = 2p/w0 = 6,28 / 3,46 = 1,81 s. à t = 0, passage en O, élastique non tendu : x = 0 : 0 = 10 cosj ; cosj =0 soit j = ½p. x(t) = 10 cos (3,46 t +½p)= 10 sin(3,46 t ) vitesse, dérivée de l'abscisse par rapport au temps : v = x' = 10 *3,46 cos (3,46 t ) v maxi = 10 *3,46 = 34,6 m/s.

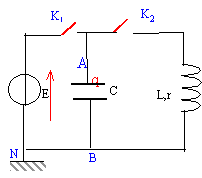
dipôle RL Un condensateur de capacité C=0,1mF est chargé grâce à une batterie de fem E=10 V et de résistance négligeable ( l'interrupteur K1 étant fermé et K2 ouvert). Calculer la charge maximale prise par ce condensateur et préciser l'armature qui est chargée positivement. Ce condensateur peut ensuite se décharger dans une bobine d'inductance L=1 H, supposée d'abord de résistance nulle. Pour cela on ouvre K1et à la date t=0, on ferme K2. - Déterminer à la date t=0, la valeur de la tension uAB et l'intensité i0 du courant dans le circuit LC. - A l'instant t la tension aux bornes du condensateur vaut uAB=uC. Etablir l'équation différentielle à laquelle satisfait uC(t). Calculer la pulsation propre w0 et la période propre T0 du circuit LC et donner l'expression de uC en fonction de t,w0 et de U0. - On visualise sur l'écran d'un oscilloscope dont le balayage horizontal du spot correspond à 0,5 ms/ cm et dont la sensibilité verticale est de 5V / cm. Représenter la courbe uC(t) que l'on observera sur l'écran de largeur 8 cm. - La bobine a, en réalité, une résistance R. Dessiner les allures des courbes possibles que l'on pourra observer sur l'écran. Quel est le rôle de R ? Données : rac carrée (10-7) = 3,2 10-4 ; rac carrée (107) = 3200; 2p rac carrée (10-7) = 2 10-3 ; corrigé QA >0 ( reliée à la borne positive du générateur) Qmax = CE = 10-7*10 = 10-6 C UAB(t=0) = E = U0 et i0=0. uC = Ldi/dt avec i = dQB/dt = -dQA/dt = -CduC/dt = -Cu'C et di/dt = -Cu"C. uC = Ldi/dt soit uC +LCu"C =0 u"C + w0² uC = 0 avec w0² = 1/(LC) = 1/(1*10-7)= 107 soit w0 = 3200 rad/s. période T0 = 2p/w0 = 6,28 / 3200 = 2 10-3 s. 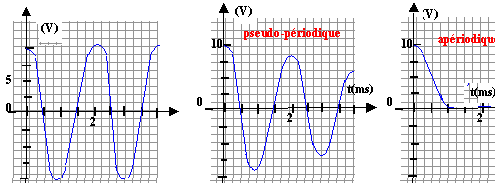uC = U0 cos (w0t) sur l'écran on observe 2 périodes ( 8 divisions fois 0,5 V/div = 4 10-3 s = 2T0) régime pseudo-périodique si R faible. régime apériodique si R grande. dans R, une partie de l'énergie du dîpôle (RLC) est dissipée par effet joule (chaleur) lors des échanges d'énergies entre condensateur et bobine.

oxydation ménagée des alcools On dispose d'un mélange de deux alcools : le propan-1-ol (noté A)et le propan-2-ol (noté B). Ecrire les formules semi-développées de ces deux alcools et préciser leur classe. On procède à l'oxydation ménagée en milieu acide, de ce mélange par une solution de dichromate de potassium en excès. On admet que A ne donne que l'acide C; B donne le corps D. Ecrire les formules semi-développées de C et D. Les nommer. Quel test permet de caractériser la fonction de D ? On donne les masses des deux alcools : mA=6g et mB=12g. - Ecrire l'équation bilan de la réaction d'oxydo-réduction de A en C. L'un des couples oxydant / réducteur est : Cr2O72- /Cr3+. - Ecrire l'équation bilan de la réaction d'oxydo-réduction de B en D - Sachant que la concentration molaire de dichromate de potassium est de 0,1 mol/L, calculer le volume minimal de la solution de dichromate de potassium qu'il faut utiliser pour l'oxydation ménagée de ce mélange des deux alcools A et B. masse atomique molaire (g/mol) C=12 ; H=1 ; O=16.   corrigé A: CH3-CH2-CH2OH propan-1-ol , alcool primaire. B: CH3-CHOH-CH3 propan-2-ol , alcool secondaire. C: CH3-CH2-COOH acide propanoïque D: CH3-CO-CH3 propanone (acétone) celle ci donne un teste positif avec la D.N.P.H et un test négatif avec la liqueur de Fehling. si oxydant en excès on obtient l'acide propanoïque 3 fois{ C3 H8 O +H2O = C3H6 O2 + 4 électrons + 4H+}. 2 fois{ Cr2O72- + 6 electrons +14 H+ = 2 Cr3+ + 7 H2O}. 3 C3 H8 O +3H2O + 2 Cr2O72- +28 H+ donne 3 C3H6 O2 + 4Cr3+ + 12 H+ + 14 H2O (1) CH3-CH(OH)-CH3 propan-2-ol 3 fois{ C3 H8 O = C3H6 O + 2 électrons + 2H+}. Cr2O72- + 6 electrons +14 H+ = 2 Cr3+ + 7 H2O 3 C3 H8 O + Cr2O72- +14 H+ donne 3 C3H6 O + 2 Cr3+ + 6 H+ + 7 H2O (2) Qté de matière : nA = 6/60 = 0,1 mol ; nB= 12/60 = 0,2 mol n (Cr2O72- ) = 2/3 *nA+ 1/3 * nB= 2/3*0,1 + 1/3*0,2 = 0,4 /3 mol n (Cr2O72- ) =[Cr2O72- ]* volume (L) d'où volume = n (Cr2O72- ) /[Cr2O72- ] = 0,4/(3*0,1) = 4/3 = 1,33 L.

acide benzoïque, benzoate de sodium.   La solubilité s( en g/L) dans l'eau d'une substance est la masse maximale de substance que l'on peut dissoudre dans 1 L d'eau. - Acide benzoïque C6H5COOH, solide blanc, monoacide faible peu soluble dans l'eau; masse molaire M=122 g/mol. - Benzoate de sodium C6H5COONa solide ionique blanc ; masse molaire M=144 g/mol - couple acide base : C6H5COOH /C6H5COO- pKa = 4,2. - indicateur coloré: rouge de crésol : zone de virage jaune [7,2 - 8,8] rouge. Donnée : 100,7 = 5. Ecrire l'équation bilan entre l'acide benzoïque et l'eau. - Rappeler la définition de la constante d'acidité du couple acide benzoïque / ion benzoate et en déduire les domaines de prédominance. - On mesure le pH d'une solution d'acide benzoïque: pH=3,5. En déduire le rapport [C6H5COOH] / [C6H5COO-] On se propose de préparer une solution S de benzoate de sodium de concentration c=0,2 mol/L à partir d'une solution S0 de benzoate de sodium de concentration C0=0,5 mol/L. Indiquer la procédure à suivre. A 10 mL de la solution S on ajoute un peu d'acide chlorhydrique concentré. On note l'apparition d'un précipité blanc. - Ecrire l'équation-bilan de la réaction mise en jeu. Calculer la constante de réaction et conclure. - Préciser le nom de ce précipité et justifier qualitativement de sa formation. On se propose de déterminer la solubilité de l'acide benzoïque à 25°C.. On pèse environ 0,4 g d'acide benzoïque et on l'introduit dans un bécher contenant 100 mL d'eau distillée. Après quelques minutes d'agitation, des petits grains restent en suspension. Une filtration permet d'obtenir la solution saturée en acide benzoïque de concentration Ca. On introduit un volume vA=10 mL de cette solution; on y ajoute quelques gouttes de rouge de crésol et on dose par une solution de soude de concentration cB=0,01 mol/L. Le rouge de crésol change de couleur pour un volume de soude versé égal à 20 mL. - Expliquer la présence de grains en suspension dans le mélange avant la filtration. - Ecrire l'équation bilan de la réaction de dosage. - Définir l'équivalence de cette réaction et en déduire la concentration molaire cA de la solution d'acide benzoïque. - Déterminer la valeur de la solubilité s de l'acide benzoïque. corrigé C6H5COOH + H2O = C6H5COO-+H3O+. Ka = [C6H5COO-][H3O+]/ [C6H5COOH] à pH <pKa, la forme acide C6H5COOH prédomine à pH=pKa, [C6H5COO-] =[C6H5COOH] à pH >pKa, la forme base C6H5COO- prédomine à pH=3,5 : pH=pKa + log([C6H5COO-] /[C6H5COOH]) log([C6H5COO-] /[C6H5COOH])= pH-pKa =3,5-4,2 = -0,7 [C6H5COO-] /[C6H5COOH]= 10-0,7 ; [C6H5COOH]/ [C6H5COO-] = 10+0,7 =5 facteur de dilution = 0,5 / 0,2 = 2,5 donc fiole jaugée de 0,1 L , pipette ou burette graduée de 0,1 /2,5 = 0,04 L= 40 mL prélever 40 mL de solution mère ( 0,5 mol/L) à la pipette + pipeteur placer dans la fiole jaugée de 100 mL compléter jusqu'au trait de jauge avec de l'eau distillée. C6H5COO-+H3O+-->C6H5COOH + H2O K =[C6H5COOH] /([C6H5COO-][H3O+]) = 1/Ka = 1/10-4,2 = 104,2 grand, donc réaction totale. précipité d'acide benzoïque très peu soluble dans l'eau à 25°C. 0,4 g dans 100 mL soit 4 g/L, valeur supérieure à la solubilité de l'acide benzoïque : donc tout le solide ne peut pas se dissoudre. C6H5COOH + HO--->C6H5COO-+ H2O à l'équivalence du titrage acide base, la qté de matière d'acide benzoïque est égale à la qté de matière d'ion hydroxyde ajouté. avant l'équivalence, l'acide est en excès ; après l'équivalence, la soude est en excès. CaVa = CbVb = 20 10-3 *10-2 = 2 10-4 mol. Ca = 2 10-4 / 10-2 = 0,02 mol/L solubilité :s = 0,02* 122 = 2,44 g/L à 25°C. retour - menu