concours d'admission à l'institut de formation de manipulateurs d'électroradiologie médicale. Caen 03

mouvement d'une balle de tennis (9points)   masse de la balle : m= 54 g ; diamètre 64 mm , volume V=137 cm3, g=9,8 m/s² , masse volumique de l'air r= 1,3 kg/m3. A. Un opérateur placé au sommet d'une tour lâche sans vitesse initiale une balle de tennis. celle-ci prend un mouvement de chute verticale le long d'un axe Oz orienté vers le bas. Origine des temps= instant où l'opérateur lâche la balle. Origine des espaces : position du centre de gravité de la balle à t=0. La balle est supposée en chute libre. Précisez ce que cela signifie ? Etablir les équations ( littérales et numériques) donnant la vitesse et la position du centre de gravité du solide en fonction de la durée t de la chute. Calculer la vitesse de la balle lorsqu'elle touche le sol situé à 100 m en dessous du point de départ. B. On se propose de vérifier si notre hypothèse simplificatrice est valable. Un dispositif non décrit permet de déterminer la vitesse réelle d'une balle de tennis lâchée dans l'air sans vitesse initiale. Les frottements de l'air sur la balle sont équivalents à une force unique variant avec la vitesse. cette force est de même direction que le vecteur vitesse et son expression est : f=kv2 où k = 10-3 S.I. Montrer que la poussée d'Archimède est négligeable par rapport au poids de la balle. Etablir l'équation différentielle ( variable v) associée au mouvement de la balle calculer la vitesse limite susceptible d'être atteinte par la balle. La balle a-t-elle atteint cette limite lorsqu'elle touche le sol après 6 s de chute ? les frottements de l'air sont-ils négligeables ? C. Un joueur de tennis utilise pour son entraînement une machine à lancer des balles. la machine propulse la balle depuis la ligne de service avec une vitesse initiale égale à 11,1 m/s. Le vecteur vitesse initial fait un angle a=45° avec l'horizontale. La balle est lancée depuis un point M situé à H=0,5 m au dessus du sol. On néglige le frottements ; la balle est soumise uniquement à son poids. Etablir l'expression litérale des équations paramètriques x(t) et y(t) du mouvement. Déterminer l'expression littérale de la trajectoir suivie par la balle Le filet de hauteur h= 0,91 m est situé à D=11,89 m de la ligne de service. La balle passe-t-elle au dessus du filet ? . corrigé chute libre : la balle n'est soumise qu'à son poids. vitesse : v = gt ; position : z= ½gt2. en éliminant le temps : t = v / g soit z = ½g (v/g)2 ou v² = 2gz. v²sol = 2*9,8*100=1960 et vsol = 44,27 m/s. poids : mg = 0,054*9,8 = 0,53 N poussée : rair V g = 1,3 *137 10-6 *9,8 = 1,74 10-3 N le poids est 303 fois plus grand que la poussée. Celle-ci est négligeable devant le poids. La balle est soumise à son poids, verticale vers le bas et aux forces de frottements sur les couches d'air,verticale, vers le haut. Ecrire la seconde loi de Newton sur un axe vertical vers le bas. mg-kv² = mdv/dt ou dv/dt +k/m v² = g vitesse limite vlim = constante donc dvlim/dt = 0 k/mv²lim =g d'où vlim = (mg/k)½=(0,054*9,8/10-3)½=23 m/s. d'après le graphe la vitesse limite est atteinte à t = 6 s ; la durée de la chute est t=6s en tenant compte des frottements au lieu de 4 s pour une chute libre. Les frottements ne doivent pas être négligés. 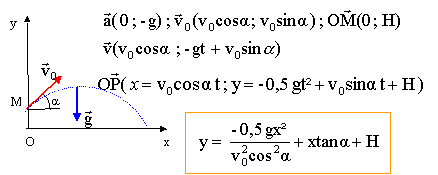y= -4,9 x² / (11,1 cos45)² + x+0,5 y= -0,08 x² + x +0,5 calcul de y pour x = 11,89 : y = -0,08*11,89² + 11,89 +0,5 = 1,08 m. valeur supérieure à h: la balle passe au dessus du filet.

radioactivité (3 points) On dispose d'une source radioactive accompagnée d'une fiche technique portant les indications suivantes : césium 137 : 13755Cs ; masse molaire 137 g/mol ; constante radioactive l = 5,63 10-2 an-1 ;radioactivité b - ; masse initiale de substance radioactive m= 2 g ; N=6,02 1023 mol-1 .   I Xe Cs Ba La Z=53 Z=54 Z=55 Z=56 Z=57 La date de fabrication de la source n'apparaît pas sur la fiche. On effectue alors une mesure de son activité totale A1 = 1,05 1012 Bq. Ecrire l'équation de désintégration de la source. Calculer le nombre initial d'atomes de césium 137 contenu dans la source. En déduire le nombre initial N0 de noyaux de césium 137 contenus dans la source. Exprimer la constante de désintégration radioactive dans l'unité du système international. Montrer que l'activité d'une source est proportionnelle au nombre de noyaux radioactifs qu'elle contient. - En déduiree la valeur de l'activité initiale A0 de la source. Déterminer l'âge de la source à l'instant où la mesure A1 a été effectué. corrigé 13755Cs -->ZAX+-10e. conservation de la charge 55= Z-1 donne Z= 56 et X est l'élément baryum Ba. conservation du nombre de nucléons 137 = A N0= 2/137*6,02 1023 = 8,79 1021 noyaux. 1 an = 365*24*3600 = 3,15 107 s d'où l = 5,63 10-2 / 3,15 107 = 1,79 10-9 s-1. activité A= -dN/dt avec N=N0e-l t ; dN/dt = N0(-l)e-l t ; A= l N. A0 = l N0 = 1,79 10-9*8,79 1021 = 15,7 1012 Bq. A=A0e-l t ; ln(A0/A) = lt ; lt = ln(15,7/1,05) = 2,7 soit t = 2,7 / 5,63 10-2 = 48 ans.

pile aluminium plomb (5 points)   élément Al Pb S N O masse molaire (g/mol) 27 207 32 14 16 1 faraday = 96 500 C On considère la pile formée en associant deux demi-piles mettant en jeu les couples Al3+/Al et Pb2+/Pb. Dans chacune des demi-piles les concentrations initiales des ions sont [Al3+]i=[Pb2+]i=1 mol/L. Les solutions S1 et S2 utlisées pour réaliser les demi-piles ont été réalisée par dissolution des composés ioniques suivants: le sulfate d'aluminium III anhydre pour l'une et le nitrate de plomb anhydre pour l'autre. On a préparé un volume V= 100 mL pour chaque solution. Justifier la formule Al2(SO4)3 des cristaux de sulfate d'aluminium puis écrire l'équation de la réaction de dissolution. - En déduire la relation entre la concentration c1 de la solution de sulfate d'aluminium et [Al3+]i. Calculer la masse m1 de sulfate d'aluminium qu'il a fallu peser pour préparer un volume V1=100 mL de solution de sulfate d'aluminium de concentration c1. Donner la formule du nitrate de plomb ainsi que l'équation de dissolution de ce solide dans l'eau. - En déduire la relation entre la concentration c2 de la solution de nitrate de plomb et [Pb2+]i. Calculer la masse m2 de nitrate de plomb qu'il a fallu peser pour préparer un volume V1=100 mL de solution de nitrate de plomb de concentration c2. On a mesuré la tension aux bornes de la pile lorssqu'elle ne débite pas UPb-Al =1,53 V positive. - Que représente la valeur de cette tension pour la pile ? - Justifier la polarité de cette pile puis donner sa représentation conventionnelle. - Quelles sont les réactions qui se produisent aux électrodes quand la pile débite ? Justifier. - Ecrire l'équation de la réaction qui se produit dans la pile lorsqu'elle débite. Cette pile débite un courant d'intensité I=200 mA pendant une durée de 2 h. - Quelle quantité d'électricité Q la pile a-t-elle débite dans ces conditions ? - En déduire la quantité de matière d'électrons ( mol) qui a transporté cette quantité d'électricité. - Calculer la variation de masse de chaque électrode. - Déterminer le concentrations finales des cations métalliques dans chaque bechers pendant ces deux heures. corrigé solide ionique électriquement neutre donc 2Al3+ et 3 SO42-. Al2(SO4)3 -->2Al3+ + 3 SO42- donc [Al3+]i= 2 C1 soit C1 = 0,5 mol/L Qté de matière de sulfate d'aluminium dans 100 mL : 0,1 C1 = 0,05 mol. masse molaire Al2(SO4)3 :27*2+3*(32+64)=324 g/mol masse m1 = 0,05*324 = 17,1g.Pb(NO3)2 -->Pb2+ + 2 NO3 - donc [Pb2+]i= C1 Qté de matière de nitrate de plomb dans 100 mL : 0,1 C2 = 0,1 mol. masse molaire Pb(NO3)2 :207+2*(14+48)=331 g/mol masse m2 = 0,1*331 = 33,1g. f.e.m de la pile = tension à vide. Le métal le plus réductuer ( Al) s'oxyde ( anode) et constitue la borne négative de la pile Al--> 3e- +Al3+ Les ions Pb2+ se réduisent à la cathode positive : Pb2+ + 2e- --> Pb bilan : 2Al + 3Pb2+ -->2 Al3+ + 3Pb - Al / Al3+ // Pb2+ / Pb + Quantité d'électricité : Q=It = 0,2*2*3600 = 1440 C Qté de matière d'électron : 1440/96500 = 0,015 mol La masse d'aluminium diminue de : 0,015/3 = 0,005 mol soit en masse : 0,005*27= 0,135 g. La masse de plomb augmente de : 0,015/2 = 0,0075 mol soit en masse : 0,0075*207 = 1,55 g. Dn(Al3+) = +0,005 mol ; n(Al3+) fin = n(Al3+) début + Dn(Al3+) =0,1+0,005 = 0,105 mol [Al3+]fin = 0,105 / 0,1 = 1,05 mol/L. Dn(Pb2+) = -0,0075 mol ; n(Pb2+) fin = n(Pb2+) début + Dn(Pb2+) = 0,1-0,0075 = 0,0925mol [Pb2+]fin = 0,0925 / 0,1 = 0,925 mol/L.

acide hypoiodique (3 points)   L'acide hypoiodique HIO appartient au couple acide base HIO / IO- de pKa1=10,6. L'ammoniac NH3 est la base du couple acide base NH4+/ NH3 de pKa2 = 9,2. On prépare V1 = 10 mL d'une solution aqueuse S1 d'acide hypoiodique de concentration c1 = 0,15 mol/L. On ajoute rapidement à cette solution V2 = 5 mL d'une solution aqueuse d'ammoniac S2 de concentration c2 = 0,1 mol/L. On suppose que les réactions de HIO et NH3 avec l'eau sont négligeables. Ecrire l'équation de la réaction acido-basique susceptible de se produire lors du mélange des solutions S1 et S2 et calculer la constante d'équilibre associée K. Calculer les quantités de matière des réactifs en présence à l'état initial. - Exprimer puis calculer le quotient de réaction initial Qr,i . - En déduire le sens d'évolution spontanée du système chimique. Exprimer Qr,éq quotient de réaction à l'équilibre et donner sa valeur. Dépend-il des conditions initiales ? Dresser le tableau d'avancement du système chimique et calculer la valeur de l'avancement à l'équilibre xéq. - Calculer le taux d'avancement final. La réaction est-elle totale ? - Calculer les concentrations des espèces chimiques présentes en solution à l'état final. corrigé HIO + NH3 = IO- + NH4+ ; K=Qr,éq= [IO-]éq[NH4+]éq / ( [HIO]éq[NH3]éq) K=Qr,éq : ne dépend que de la température. NH4++ H2O= H3O+ + NH3 ; Ka2 = [NH3]éq [H3O+]éq/ [NH4+]éq d'où [NH4+]éq / [NH3]éq = [H3O+]éq/Ka2 HIO + H2O= H3O+ + IO- ; Ka1 = [ IO-]éq [H3O+]éq/ [HIO]éq d'où [IO-]éq / [HIO]éq = Ka1/[H3O+]éq. K= Ka1 / Ka2 = 10-10,6 / 10-9,2 = 10-1,4 = 0,04. [NH3]i=V2C2/(V1+V2)=5*0,1/15= 0,0333 mol/L [HIO]i=V1C1/(V1+V2)=10*0,15/15= 0,1 mol/L [IO-]i=[NH4+]i =0 Qr,i= [IO-]i[NH4+]i / ( [HIO]i[NH3]i)=0; valeur inférieure à K: évolution dans le sens direct. NH3 +HIO = IO- + NH4+ initial 0,5 mmol 1,5 mmol 0 0 en cours 0,5-x 1,5-x x x à l'équilibre 0,5-xéq 1,5-xéq xéq xéq K=0,04 = x2éq/((0,5-xéq)(1,5-xéq)) (0,5-xéq)(1,5-xéq) = 25x2éq ; 24x2éq + 2xéq-0,75 = 0 résoudre : xéq = 0,14 mmol xmax= 0,5 mmol et le taux d'avancement final vaut t = 0,14/0,5 = 0,28. ( réaction partielle) [IO-]fin=[NH4+]fin =0,14/15 = 9,310-3 mol/L [HIO]fin= (1,5-0,14)/15=0,091 mol/L [NH3]fin= (0,5-0,14)/15=0,024 mol/L

retour - menu