concours kiné Assas 03 physique 1 h - 20 points- chimie ½ h- 10 points. il est demandé l'expression littérale avant tout calcul

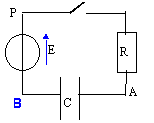
dipôle RC : charge d'un condensateur ; bilan énergétique On considère le circuit suivant comprenant, montés en série : un générateur de tension continue de fem E=6 V et de résistance interne nulle, une résistance R=5 kW, un condensateur de capacité C=1,2mF et un interrupteur K. Etude de la charge : Préciser sur le schéma du montage, le sens positif choisi pour l'intensité du courant i. Etablir l'équation différentielle de charge liant la tension instantanée uAB(t) aux bornes du condensateur et sa dérivée par rapport au temps duAB/dt en fonction de R, C et E. Vérifier que l'expression uAB(t) = E(1-e-t/(RC)) est solution de l'équation différentielle trouvée précédemment. La tension initiale du condensateur uAB(t=0)=0 est-elle compatible avec les données de l'exercice ? Quelle est la valeur maximale que peut atteindre la tension uAB(t) ? Donner la dimension du produit RC. Comment appelle-t-on ce produit ? Quelle est sa signification pratique pour ce circuit ? Calculer la valeur de la tension instantanée aux instants t=5 ms, t=10 ms, t=20 ms et t=50 ms. Tracer l'allure de la tension uAB(t) Déterminer l'expression de l'intensité du courant i(t) en fonction du temps t et des paramètres E, R et C. Calculer sa valeur numérique à l'instant t=0.. Lorsque t est très grand, que vaut l'intensité du courant ? Bilan énergétique : Quelle est l'expression, en fonction de E et C de l'énergie électrique WC emmagasinée dans le condensateur lorsque la charge est terminée ? La puissance électrique instantanée délivrée par le générateur est p(t) = dWel /dt = Ei(t). Déterminer l'énergie électrique totale Wel délivrée au circuit par le générateur au cours de la charge en fonction de E et C. Déduire des deux questions précédentes l'expression WR, de l'énergie dissipée dans la résistance R au cours de la charge. 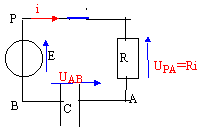corrigé uPB= E ; uPB= uPA+ uAB avec i = dqA/dt = CduAB/dt . E= Ri +uAB soit E=RC duAB/dt +uAB (1) dériver l'expression de uAB par rapport au temps : duAB/dt = E/(RC) e-t/(RC). repport dans (1) : E= RC*E/(RC) e-t/(RC)+E(1- e-t/(RC)) E = Ee-t/(RC) + E-E e-t/(RC) égalité vérifiée. uAB (t=0)= E(1-e0) = E(1-1)=0 condensateur initialement non chargé. uAB (t=oo)= E(1-0) =E condensateur entièrement chargé. t =RC = 5 103*1,2 10-6 = 5 10-3s = 5 ms constante de temps en seconde. Au bout de 5t le condensateur est considéré comme chargé. 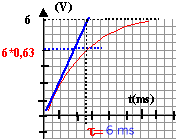t = 5ms t=10 ms t= 20 ms t= 50 ms uAB =6(1-0,37) =3,78 V uAB= 4,87 V uAB= 5,78 V uAB= 6 V i = CduAB/dt = C E/(RC) e-t/(RC)= E/R e-t/(RC). à t=0 l'intensité vaut : 6/5000 e0 = 6/5000 = 1,2 mA. au bout d'un temps infini l'intensité est nulle. 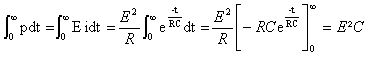énergie stockée par le condensateur chargé : WC= ½CE² énergie fournie par le générateur : Wel = WC+WR d'où WR= ½CE²

mouvement du centre d'inertie d'une mini-fusée Dans un club amateur, on étudie la trajectoire d'un modèle réduit de fusée. La fusée pourra être considérée comme une masse ponctuelle M ramenée en son centre d'inertie et on ne tiendra pas compte de la résistance de l'air. Dans un premier temps, la fusée est lancée horizontalement depuis un point O, à une date t=0, avec un vecteur initial v0, dans un domaine limité où le champ de pesanteur est uniforme et a pour intensité g0 = 9,81 m/s². On étudie le mouvement du centre d'inertie de la fusée dans un repère terrestre (Ox,Oz), Ox est l'axe horizontal de même sens et direction que la vitesse initiale. Oz est l'axe vertical orienté vers le bas. Exprimer le vecteur accélération de la fusée dans le repère choisi. Etablir sous forme littérale, les équations exprimant les coordonnées x(t) et z(t) de la fusée en fonction du temps lors du mouvement dans le repère choisi. En déduire l'expression littérale de la trajectoire de la fusée. Déterminer numériquement les coordonnées de la fusée à la date t=2s si v0=5 km/s. Dans un second temps, au sommet du mont Everest de hauteur h, on fait décrire à la fusée une orbite circulaire, dont le centre est le centre de la terre, en lui donnant une vitesse suffisante v1. L'expression du champ de pesanteur à l'altitude h est donné par : g = g0 R² / (R+h)² avec R= 6,38 106 m Que peut-on dire du vecteur accélération de la fusée ? En déduire que son mouvement est uniforme de vitesse v1. Etablir l'expresion littérale de la vitesse v1 de la fusée en fonction de g0, h et R. Calculer la valeur de v1 si h = 8,85 103 m. Quelle est la valeur numérique de la période T du mouvement de la fusée ? 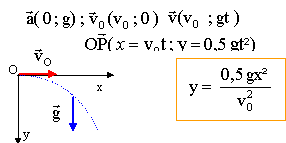corrigé x(t=2) = 5000*2 = 104 m ; y(t=2) = 0,5 *4*9,8 = 19,6 m. La fusée n'est soumise qu'à la force de gravitation de la terre, force centripète; cette force est perpendiculaire à la vitesse; en conséquence elle ne travaille pas et ne modifie pas l'énergie cinétique. Donc la valeur de la vitesse est constante et le mouvement est uniforme. a=g0R²/ (R+h)² = v1² / (R+h) d'où v1² = g0R²/ (R+h) v1² =9,8(6,38 106)² / (6,38 106 + 8,85 103) = 62,43 106 soit v1 = 7,9 103 m/s. La circonférence de rayon (R+h) est parcourue à la vitesse v1 durant une période T 2p(R+h)=v1T soit T= 2p(R+h)/v1 T= 6,28*(6,38 106 + 8,85 103) / 7,9 103 = 5 103 s.

transformations nucléaires L'iode 131 13153I est un radionucléide ayant la propriété de se fixer sur la glande thyroïde. Il présente une radioactivité de type b-. Donner la composition du noyau d'iode 131. Lors de la désintégration b-, quelle transformation se produit dans le noyau d'iode 131 ? Ecrire l'équation de cette transformation. Ecrire l'équation de la réaction de désintégration b- de l'iode 131 et préciser les lois de conservation utilisées. Antimoine Sb: Z= 51 ; tellure Te Z=52 ; Xénon Xe Z=53 ; Césium Cs Z=55. Une personne a été contaminée par de l'iode 131 dont le temps de demi-vie ou période est T=8 jours. - Définir en une phrase le mot demi-vie. - Le nombre N(t) de noyaux non désintégrés au bout d'un temps t est donné par N(t) = N0 e-lt où N0 est le nombre de noyau d'iode 131 à l'instant t=0 et l une constante radioactive. Déterminer l'expression de la constante radioactive l en foncrtion de la période T et calculer sa valeur numérique. Pour la personne contaminée à l'instant t=0, calculer le temps au bout duquel il ne restera plus que 1/126 ème du nombre de noyaux d'iode 131 initial fixés sur la glande thyroïde. corrigé 53 protons et 131-53 = 78 neutrons un neutron se transforme en proton : 01n-->11p + -10e 13153I --> AZX + -10e conservation de la charge : 53=Z-1 d'où Z=54 élément Xe conservation du nombre de nucléons : 131=A+0. Le temps de demi-vie ou période est la durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés. à t=T, N(T)=½ N0= N0e-lT soit 0,5 = e-lT ou ln2 = lT ; l =ln2 / T = 0,693 / 8 = 0,0866 jour-1. 128 est égal à 27 donc au bout de 7 périodes ou 56 jours le nombre de noyaux initial est divisé par 128.

réaction entre l'éthanol et le sodium pur   Dans 30 mL d'étanol on introduit 1 g de sodium. La réaction qui se produit est assez vive et donne des ions éthanolate CH3CH2O-, des ions sodium Na+ et du gaz dihydrogène H2. a- Ecrire l'équation chimique de la réaction entre l'éthanol et le sodium. b- Montrer que tout le sodium a réagi. c- En déduire le nombre de moles d'ion éthanolate formés au cours de la réaction. Après refroidissement du mélange réactionnel, on le verse dans une fiole jaugée de 200 mL et on complète avec de l'eau disssstillée. La solution ainsi obtenue est appelée S, son volume est noté V. a- L'ion éthanolate étant une base, écrire l'équation chimique de la réaction des ions éthaolate avec les molécules d'eau. b- On donne v= 10 mL de solution S par une solution d'acide chlorhydrique de concentration Ca = 0,2 mol/L. L'équivalence acido-basique est obtenue lorsqu'un volume va = 10,7 mL d'acide a été ajouté. Montrer que ce résultat est en accord avec la réponse obtenue en 1c. Justifier. masse atomique molaire (g/mol) Na=23 ; C=12 ; H=1 ; O=16. masse volumique de l'éthanol r =790 kg/m3. corrigé CH3CH2OH + Na -->CH3CH2O- + Na+ +½H2. Quantité de matière initiale : sodium 1/23 = 0,0435 mol éthanol : 30*0,79 = 23,7 g puis 23,7 / (12*2+6+16) =0,515 mol l'éthanol est en excès, le sodium en défaut. il se forme donc 0,0435 mol d'ion éthanolate et 0,0435 mol éthanol a réagi. CH3CH2O- + H2O-->CH3CH2OH+HO- à l'équivalence du dosage acide base : CaVéqui = [HO-] v soit 0,2*10,7 = 2,14 mmol d'ion HO- dans 10 mL de S soit 2,14*200 /10= 42,8 mmol d'ion HO- ( ou d'éthanol) dans 200 mL de S 0,0428 mol éthanol a réagi avec le sodium résultat très proche de 0,0435 mol trouvé ci-dessus.

oxydo-réduction et catalyse   Dans une solution d'iodure de potassium (K+ ; I-) on verse une solution de peroxodisulfate de sodium ( 2Na+ ; S2O82-). La réaction est théoriquement possible mais on n'observe rien. Expliquer pourquoi. On ajoute quelques cristaux de sulfate de fer II FeSO4. On observe alors un changement de couleur de la solution. Une analyse montre que la concentration en ions Fe2+ n'a pas varié après la réaction. a- Expliquer le processus ayant conduit à ce changement de couleur. b- Ecrire les équations chimiques des réactions qui se sont produites. Quel est le rôle joué par les ions Fe2+? couples oxydant/ reducteur : S2O82-/ SO42- ; I2/I- ; Fe3+/ Fe2+. corrigé On n'observe rien car la réaction est lente à 20°C. Le catalyseur Fe2+ accélére la réaction: une réaction lente est remplacée par deux réactions rapides. S2O82-+2e-= 2SO42- réduction 2Fe2+= 2Fe3+ + 2e- oxydation S2O82-+2Fe2+-->2SO42- +2Fe3+ oxydo-réduction rapide. 2I-= I2+ 2e- oxydation 2Fe3+ + 2e- =2Fe2+ réduction 2I- +2Fe3+--> I 2+2Fe2+ rapide, le catalyseur est régénéré.

retour - menu