d'après concours kiné St Michel 03 physique 1 h (note sur 20 ) - chimie ½ h (note sur 10) Donner pour chaque question la (les) proposition(s) exacte(s) les points ne seront accordés que si la réponse globale est correcte ( sans calculatrice) Données : 20,5 = 1,41 ; 30,5 = 1,73 ; p=3,14 ; sin 45 =cos 45= 0,707 ; sin 60 =0,87 ; cos 60 = 0,5 ; G =6,62 10-11 SI rayon de la terre R= 6400 km ; célérité de la lumière dans le vide c=3 108 m/s ; g0=10 m/s²

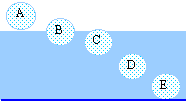
questions 1 à 4 Soit l’expérience idéale suivant : on dispose d’une baignoire remplie d’eau  et d’un ballon sphérique également rempli d’eau. La masse de l’enveloppe est considérée comme négligeable. On laisse choir doucement le ballon dans la baignoire sans lui communiquer de vitesse particulière. - Parmi les positions suivantes laquelle vous semble correspondre à l’équilibre hydrostatique.   Cette même expérience est réalisée sur la lune. Même question. Cette expérience est réalisée dans la station spatiale internationale. Même question. Donner (l’) ou (les) affirmations exacte(s) A- La poussée d’Archimède subie par un corps dans un fluide dépend de la profondeur d’immersion. B- La poussée d’Archimède dépend de l’état de mouvement du corps immergé par rapport au fluide. C- La poussée d’Archimède est indépendante de la profondeur d’immersion et de l’état de mouvement du corps par rapport au fluide. D- La poussée d’Archimède est une force de nature électromagnétique. E- La poussée d’Archimède est une force de nature gravitationnelle. corrigé le ballon est soumis à deux forces : son poids, vertical, vers le bas , valeur : volume du ballon * masse volumique de l'eau * g = Vreaug la poussée d'Archimède, vertical, vers le haut, valeur = poids du volume d'eau déplacé poussée = volume du ballon immergé * masse volumique du liquide * g = Vireaug à l'équilibre hydrostatique, ces deux forces sont opposées(Vreaug = Vireaug ) : le ballon s'enfonce donc jusqu'à ce qu'il soit entierement immergé situation B correcte. même conclusion sur la lune.au voisinage du centre de gravité de la station orbitale , il y a impesanteur dans un référentiel lié à la station. : en lachant le ballon au desus du liquide, le ballon reste là où on le lache. situation A correcte. C- La poussée d’Archimède est indépendante de la profondeur d’immersion et de l’état de mouvement du corps par rapport au fluide. vrai

ondes Les géophysiciens ont mis en évidence l’existencede deux parties concentriques dans le noyau de la terre. Le noyau interne Ni et le noyau externe Ne. Le premier, la graine du noyau se comporte plutôt comme un solide et le second se comporte plutôt comme un fluide ; c’est ce que l’on appelle l’anomalie du noyau. Donner (l’) ou (les) affirmations exacte(s) : A- Le Ni se laisse difficilement traverser par les vibrations longitudinales. B- Le Ni se laisse facilement traverser par les vibrations longitudinales. C- Le Ni se laisse difficilement traverser par les vibrations transversales. D- Le Ni ne se laisse traverser ni par les unes ni par les autres. E- Le Ni se laisse facilement traverser par les vibrations transversales. Donner (l’) ou (les) affirmations exacte(s) : A- Le Ne se laisse difficilement traverser par les vibrations  transversales. B- Le Ne se laisse difficilement traverser par les vibrations  longitudinales. C- Le Ne se laisse facilement traverser par les vibrations transversales. D- Le Ne ne se laisse traverser ni par les unes ni par les autres. E- Le Ne se laisse facilement traverser par les vibrations longitudinales. Le hasard veut que lors de la plongée d’un sous marin nucléaire, celui-ci se retrouve à la verticale de l’épicentre d’un tremblement de terre, situé en profondeur dans le sol océanique. L’épicentre émet des trains d’ondes sismiques, formées par superposition de deux composantes, l’une longitudinale (onde P), l’autre transversale(onde S) Donner (l’) ou (les) affirmations exacte(s) : A- Le sonar du sous marin ne détecte que les ondes S. B- Le sonar du sous marin ne détecte que les ondes P. C- Le sonar du sous marin détecte les ondes P et les ondes S. D- Le sous marin va osciller verticalement lors du passage des ondes sismiques. E- Le sous marin oscillera verticalement et horizontalement. corrigé Les vibrations longitudinales se propagent dans les liquides et les solides Les vibrations transversales se propagent dans les solides. 5/ B et E vraies. 6/ A et E vraies. 7/ B et D vraies.

mécanique   Dans un modèle simplifié de circulation sanguine, on fait l’hypothèse que le cœur fournit l’énergie suffisante pour permettre au sang d’arriver au cerveau, en présence uniquement d’un champ de pesanteur g. La masse volumique du sang est voisine de celle de l’eau (1000 kg/m3) et le débit sanguin cérébral est de l’ordre de 300 L/h. Sachant que la distance entre le cerveau et le cœur est de 50 cm, la puissance cardiaque mise en jeu pour l’irrigation du cerveau, chez un individu debout, est en watt. 0,22 ; 0,42 ; 0,62 ; 0,82 ; 1,22 ; autres. La force motrice d’une locomotive est de 8 105 N, sa puissance est de 4 104 W ; par conséquent elle roule à la vitesse de 160 km/h. vrai ou faux. Un satellite orbite autour de la terre avec une apogée (point le plus haut de sa trajectoire) situé à un rayon terrestre. Par conséquent, la valeur du champ de gravitation crée par la terre en ce point est en m/s² 2,25 ; 2,5 ; 3,25 ; 4 ; 4,5 ; autres. Un wagonnet de montagnes russes de masse m= 1 tonne avec ses passagers, décrit un cercle vertical de rayon 6,4 m. Sa vitesse minimale au sommet de la trajectoire est en m/s. 6 ; 8 ; 9 ; 10 ; 11 ; autres. Un mobile de masse m = 50 kg descend une pente de 5% en partant sans vitesse initiale. La vitesse atteinte au bout de 100 m de descente est de 36 km/h. Il a donc été soumis à des forces de frottements, au cours de la descente, forces supposées constantes et de valeur égale à (N) : 0 ; 36 ; 18 ; 56 ; 62 ; autres. On étudie le mouvement d’un canot à moteur et en particulier l’évolution de sa vitesse en fonction du temps. Pour cela et dans un souci de simplification, le canot est assimilé à un point sur lequel agissent les forces : - le poids du canot P=mg - La réaction du plan d’eau sur le canot ( R) - La force motrice du moteur (F) - La force de frottement fluide directement proportionnelle à la vitesse du canot ( f = -k v) L’équation différentielle de la vitesse peut se mettre sous la forme : at-v0 ; v0 sin ( wt-j)  ; v0 (1 – e–t/t ) ;  v0 e–t/t ;  v0 (1 + e–t/t) ; autres. Une bouée de masse m et de volume V est retenue au fond d’un bassin rempli d’eau, de masse volumiqueconstante r0. La profondeur du bassin est suffisante pour la suite de l’expérience correspondant à l’étude du mouvement d’ascension  de la bouée. Nous nous plaçons dans le cas où les forces de frottements entre la bouée et l’eau sont de la forme f =  -kv. Donner (l’) ou les affirmation(s) exacte(s) : A- Le mouvement est uniforme pendant toute la durée de l’ascension. B-  Le mouvement est uniforme pendant une partie de l’ascension. C- Le mouvement est uniformément décéléré. D-Son expression mathématique est v(t) = v0 e–t/t   . E- Son expression mathématique est v(t) = v0 (1- e–t/t  ). E- Son expression mathématique est v(t) = v0 (1+ e–t/t  ). Dans les expressions mathématiques précédentes apparaissent les grandeurs v0 et t. Elles sont données par les expressions suivantes : v0 = mVgr0 / k ; v0 =(m + Vr0 )g / k ; v0 =(-m + Vr0 )g / k ; t= k/m ; t = m/k. Un athlète a parcouru un 100 m en 10,5s. On modèlise sa course en considérant 2 phases : il accélère uniformément pendant les 15 premièrs mètres de course, qu'il parcourt ensuite à vitesse constante de 10 m/s jusqu'à l'arrivée. - Quelle est la valeur de l'accélération moyenne (m/s²) pendant la phase de démarrage ? 0,95 ; 0,12 ; 9,5 ; 5 ; 6,7 ; 4,3. corrigé débit = 300/3600 = 3/36 = 1/12 L/s puissance (W) mise en jeu par le coeur = travail du poids de 1/12 L de sang P= mgh = 1/12 * 10*0,5 = 5/12 = 0,42 W. Puissance (W) = force (N) * vitesse (m/s) vitesse = puissance / force = 4 104 / 8 105 = 1 / 20 = 0,05 m/s = 0,05*3,6 km/h =0,18 km/h. à l'altitude h = rayon terrestre noté R, g = 10 R² / (R+R)² = 10 / 4 = 2,25 m/s². au sommet de la trajectoire, le wagonnet est soumis à deux forces centripètes, le poids et l'action normale du support. A la limite du décrochement l'action du support notée N, est nulle. la seconde loi de Newton s'écrit : mg + N = mv²/ r v²mini = gr = 10*6,4 = 64 ; vmini = 8 m/s. 36 km/ h = 36/3,6 m/s = 10 m/s théorème de l'énergie cinétique : ½mv²-0 = travail du poids + travail des frotements l'action normale du plan, perpendiculaire à la vitesse ne travaille pas ½mv² = mgh -fAB avec AB = 100 m et h = 0,05*100 = 5 m f = m(gh-½v²) / AB = 50(10*5 - 0,5 * 10²) / 100 =0. les relations proposées ne sont pas des équations différentielles mais les solutions d'équations différentielles. Poids du canot et action normale de l'eau sont opposées. La seconde loi de Newton s'écrit, projetée sur un axe horizontal, de même sens que la vitesse. F-kv = ma = mdv/dt = mv' soit v' + k/m = F/m. La bouée est soumise à : son poids, vertical vers le bas , valeur mg la poussée d'Archimède, poids du volume d'eau déplacé, verticale vers le haut , valeur : Vr0g les frottements, verticale, de sens contraire à la vitesse , valeur : kv la seconde loi de Newton s'écrit sur un axe vertical vers le haut : -mg + Vr0g -kv = ma = mdv/dt = mv' v' + k/m v = g(Vr0/ m -1) (1) Le mouvement est uniforme pendant une partie de l’ascension. La vitesse limite est telle que : k/m vlim = g(Vr0/ m -1) soit vlim = g m/k(Vr0/ m -1)= g/k(Vr0-m) solution de l'équation différentielle (1) : v = A e-t/t+vlim avec t = m/k. à t=0 , la vitesse est nulle d'où 0 = A +vlim soit A = -vlim ; v = vlim ( 1-e-t/t). accélération moyenne amoy = Dv/Dt avec Dv = 10 m/s 100-15 = 85 m parcouru à la vitesse de 10 m/s soit une durée de 85/10 = 8,5 s Dt = 10,5-8,5 = 2s et amoy = Dv/Dt = 10/2 = 5 m/s².

optique Un objet de 2 m de hauteur est regarder à travers une lentille de vergence v= 2 dioptries et situé à 500 m de celle-ci. L’image de l’objet est donc située à : A- 40 cm à droite de la lentille. B- 50 cm à droite de la lentille. C- 60 cm à droite de la lentille. D- 50 cm à gauche de la lentille. E- 40 cm à gauche de la lentille. F- autres. L’image précédente a une taille de ( en mm) 2 ; 3 ; 4 ; 5 ; 6 ; autres. Cette même image : A- est droite par rapport à l’objet et réelle. B- est droite par rapport à l’objet et virtuelle. C- est renversée par rapport à l’objet et réelle D- est renversée par rapport à l’objet et virtuelle E- se forme à l’infini. Le rapprochement dioptrique produit par une couche de benzène de 30 cm d’épaisseur et d’indice de réfraction n=1,5 est de (en cm) : 4 ; 5 ; 8 ; 10 ; 15 ; autres. Pour obtenir le même rapprochement mais avec de l’eau d’indice n = 1,33, l’épaisseur de la couche devrait être en mm : 20 ; 30 ; 40 ; 50 ; 60 ; autres. 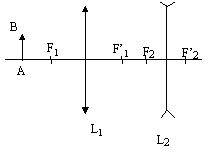Soit le système optique suivant : F1 et F’1 sont les foyers de L1 ; F2 et F’2 sont les foyers de L2 ; L’image par construction donnée de l’ensemble est : A- virtuelle et renversée par rapport à AB. B- virtuelle et droite par rapport à AB. C- réelle et renversée par rapport à AB. D- réelle et droite par rapport à AB. 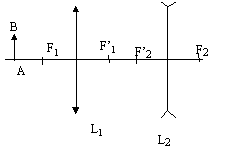Soit le système optique suivant : F1 et F’1 sont les foyers de L1 ; F2 et F’2 sont les foyers de L2 ; L’image par construction donnée de l’ensemble est : A- virtuelle et renversée par rapport à AB. B- virtuelle et droite par rapport à AB. C- réelle et renversée par rapport à AB. D- réelle et droite par rapport à AB. corrigé objet considéré à l'infini : l'image se trouve au foyer principal image vergence v = 2dioptries, d'où la distance focale image 1/2 = 0,5 m image réelle, inversée par rapport à l'objet, située à 50 cm à droite de la lentille.  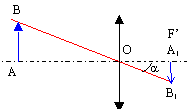tan a = AB/OA = 2/500 ; tan a =A1B1/OF' soit A1B1= OF'tan a = 0,5 * 2/500 = 1/500 = 0,002 m = 2 mm. déplacement de l'image par la couche de benzène : d= e(1-n0/n) avec n0 =1, indice de l'air ; e épaisseur de la couche en m. d = 0,3(1-1/1,5) = 0,3*0,5/1,5 = 0,1 m = 10 cm. épaisseur de la couche d'eau : 0,1 = e(1-1/1,33) = e*0,33/1,33 soit e = 0,1*1,33/0,33 = 0,4 m = 40 cm = 400 mm. 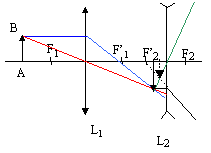l'image définitive est renversée par rapport à AB ; elle est située à gauche de la seconde lentille et en conséquence est virtuelle

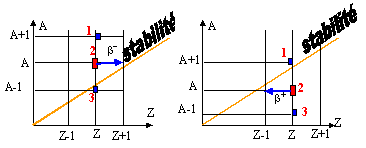
radioactivité   Soient les trois radionucléides suivants : A-1 ZX (1) ; A ZX (2) ; A+1 ZX (3). A ZX  est émetteur b-. Ces trois radionucléides sont classés par ordre croissant de stabilité. La bonne combinaison est : 3,2,1 ; 3,1,2 ; 2,1,3 ; 2,3,1 ; 1,3,2. Soient les trois radionucléides suivants : A+1 ZX (1) ; A ZX (2) ; A-1 ZX (3). A ZX  est émetteur b +. Ces trois radionucléides sont classés par ordre croissant de stabilité. La bonne combinaison est : 3,2,1 ; 3,1,2 ; 2,1,3 ; 2,3,1 ; 1,3,2. Dans le texte qui suit une ou plusieurs erreurs ont été volontairement introduites. Combien d’erreurs ? …..L’uranium naturel extrait du minerai est constitué de 99,3 % d’uranium 238 et de seulement 0,7 % d’uranium 235, seul susceptible de fournir de l’énergie par fission. C’est donc un combustible très pauvre. c’est la raison pour laquelle dans presque la totalité des réacteurs nucléaires d’aujourd’hui on utilise de l’uranium enrichi à 3 ou 4% en uranium 235. Dans un réacteur la fission des noyaux d’uranium 235 conduit à la formation de noyaux radioactifs appelés produits de fission.. La capture de neutrons par l’uranium 238 produit après deux désintégrations b- au plutonium 238 qui peut aussi fournir de l’énergie par fission. Seule une infime partie du combustible placée dans un réacteur est désintégrée. L’uranium qui n’a pas été consommé et le plutonium formé sont récupérés après séparation des produits de fission. Ce que l’on appelle le retraitement.. L’uranium et le plutonium sont recyclés pour produire à nouveau de l’électricité, d’où la raison du cycle du combustible. On rappelle que le noyau d’uranium contient 92 protons et que celui de plutonium 94.   corrigé A ZX  est émetteur b- : A ZX  -->A Z+1X  + -10e A ZX  est émetteur b+ : A ZX  -->A Z-1X  + +10e dans le cas de l'émission b- : 3, 2, 1; (3 est le plus proche de la zone de stabilité et 1 le plus loin) dans le cas de l'émission b+ : 1, 2, 3; (1 est le plus proche de la zone de stabilité et 3 le plus loin) ....seul susceptible de fournir de l’énergie par fission...... ....Seule une infime partie du combustible placée dans un réacteur est désintégrée.... ces affirmations sont fausses car l'uranium 238 non fissible est fertile : ce dernier bombardé par des neutrons conduit à des réactions de fission.

chimie   A- dans le domaine de la vie la respiration des êtres vivants est une transformation forcée. B- Lorsqu’une pile fonctionne, le système chimique qui la constitue est hors équilibre. C- La charge d’un accumulateur est une transformation forcée. D- l’acide chlorhydrique est capable d’attaquer tous les métaux. E- Dans un électrolyseur la cathode est l’électrode reliée au pôle positif du générateur. A- Le mouvement brownien est le témoin de l’agitation moléculaire au sein d’un solide. B- Si les chocs entre molécules de gaz sont élastiques, les chocs sont efficaces. C- La fréquence des collisions diminue si la concentration des réactifs diminue. D- Le temps de demi réaction correspond à la moitié de la durée totale de la réaction. E- Un catalyseur n’augmente pas le nombre de collisions efficaces. A- La température est sans effet sur le taux d’avancement à l’équilibre d’une estérification. B- L’aspirine donne de l’acide salicylique par hydrolyse basique. C- Les savons sont des tensioactifs efficaces en eaux dures. D- L’obtention d’alcanes ramifiés à partir d’alcanes linéaires se fait par craquage catalytique. E- le reformage permet d’obtenir des hydrocarbures benzéniques. A- Certaines espèces chimiques comme l’eau possède un caractère amphiphile. B- La constante d’équilibre d’une réaction dépend des conditions initiales du système. C- Le changement d’état s’accompagne de rupture de liaisons intramoléculaires. D- La rupture d’une liaison chimique est exothermique. E- Au cours d’une liquéfaction il y a augmentation du désordre dans le système. Le bromure de méthyle réagit avec l’eau suivant l’équation totale : CH3Br + H2O --> CH3OH + Br - + H+. Une cellule de longueur L et de surface S reliée à un conductimètre plonge dans un bécher contenant initialement 10 mol d’eau, 10 mmol de bromure de méthyle et un solvant homogénéisant l’ensemble. La réaction est suivie par relevé conductimétrique. A- La conductivité d’une solution électrolytique augmente si la température augmente. B- La conductivité d’une solution électrolytique est l’inverse de sa résistance. C- La conductivité d’une solution électrolytique varie avec la surface de la cellule. D- La réaction chimique étudiée ici est une réaction d’élimination. E- Si cette réaction était étudiée à deux températures différentes, l’avancement final serait différent Lorsque le taux d’avancement est de 10%, la conductance de la solution est : 13,3 mS; 0,215 S ; 2,15 S ; 215 mS ; 2,15 mS. l(H+) = 35 10-3 ; l (Br-) = 8 10-3 S m² mol-1 ; volume de la solution V=200 mL ; rapport de la cellule L/S=100 m-1. cours d’une autre manipulation la conductivité mesurée à un instant t était 430 mSm-1, l’avancement de la réaction serait : 0,02 dmol ; 1 mmol ; 0,2 cmol ; 0,1 cmol ; 2 mmol Quantités initiales : 20 mmol de bromure de méthyle ; 10 mol d’eau conductivité finale mesurée 4,3 S m-1. Le peroxyde d’hydrogène H2O2 réagit lentement avec les ions iodures I- en solution aqueuse acide suivant la réaction quasi-totale d’équation : H2O2 + 2I- --> I2 + 2H2O. L’évolution de la concentration en diiode est suivie par spectrophotométrie. Le spectrophotomètre comporte une cuve de longueur L= 10 mm. Le coefficient d’extinction molaire est e =2 105 L mol-1 cm-1. Le mélange initial est incolore. A- L’absorbance de cette solution est définie par la loi de Berr Lambert A= e / L [I2] B- Cette manipulation s’effectue à une longueur d’onde déterminée. C- Le coefficient d’extinction molaire ne varie pas avec la longueur d’onde utilisée. D- La solution est nécessairement colorée par le diiode. E- Le réglage du zéro de l’appareil s’effectue avec une cuve contenant de l’eau et du diiode. L’absorbance mesurée au temps de demi réaction est : 1 ; 0,1 ; 1,5 ; 2 ; 0,2 concentrations initiales dans la cuve en mol /L :[H2O2]=2 10-3 ; [I-]=210-5 ; [H+]=2 10-3. Si l’avancement varie de manière linéaire, de l’instant t à la date t=10 s, la vitesse initiale volumique de la réaction est en mol –1 s-1 : 2 10-5 ; 2 10-7 ; 10-7 ; 10-6 ; 4 10-7. La concentration des ions iodures disparue à la date t=10 s est 2 10-6 mol/L. Une solution S est obtenue par mélange de 4 solutions dont les caractéristiques initiales sont les suivantes/ composé formule volume concentration initiale (mol/L) méthanoate de sodium HCOO- Na+ V1=50 mL C1=0,02 acide méthanoïque HCOOH V2=50 mL C2=0,02 acide nitreux HNO2 V3=50 mL C3=0,02 nitrite de sodium Na+ NO2- V4=50 mL C4=0,02 Soit l’équation acido-basique pouvant se produire : HCOO- + HNO2= NO2- + HCOOH HCOOH/ HCOO- : pKa = 3,8 ; HNO2 / NO2-  ;pKa = 3,2. A-  Le quotient de réaction initiale est de 10. B- Le système évolue dans le sens direct. C- Le quotient de réaction à l’équilibre est 4. D- Si le pH à l’équilibre est 2,5, l’espèce HCOO- prédomine par rapport à HCOOH. log 4 = 0,6 ; log 2,5 = 0,4 L’instant t où la concentration [NO2-] dans la solution vaut 6 mmol/L, l’avancement de la réaction est : 0,02 mol ; 0,2 mmol ; 2 cmol ; 0,2 dmol ; 2 mmol. Si l’vancement final est 1/ 3 mmol, le pH de la solution S est : 3,5 ; 3,2 ; 3,8 ; 4,1 ; 2,9. log 5 = 0,7 et log 2 = 0,3. corrigé 1B et 1C vraies. 2C vraie. t½ : durée au bout de laquelle la moitié du réactif limitant à disparu ( ou encore durée au bout de laquelle l'avancement est égal à ½ xfin ) Le catalyseur remplace une réaction lente par deux réactions plus rapides. 3 : amphiphile (ion carboxylate des savons possédant une extrémité lipophile et une partie hydrophile) le reformage catalytique donne des alcanes ramifiés 3A vraie. 4 faux. 5A  est vraie. La conductance en siemens est l'inverse de la résistance G=1/R ; la conductance dépend de la cellule de mesure; la conductivité est indépendante de la nature de la cellule. conductance G (en S) et conductivité s( S /m) sont proportionnelles; la constante de proportionnalité dépend de la surface de la cellule. il s'agit d'une réaction de substitution. s = l (H+) [H+]+ l (Br-) [Br-]  avec [H+] =[Br-]  = t c ; c = 10-3 / 0,2 = 5 10-2 mol/L = 50 mol/m3; t = 0,1. s =(35 + 8) 10-3 *0,1*50 = 0,215 S / m. G (S)= k(m) s (S/m) = 0,01*0,215 = 2,15 10-3 S = 2,15 mS. s t = 0,43 S/m ; s fin = 4,3 S/m ; or t = s t / s fin =0,1 avancement x = t x fin = 0,1 *20 10-3 = 2 10-3 mol = 2 mmol = 0,2 cmol = 0,02 dmol. A= e L [I2] ;(L en cm ) 6B et 6D vraies. H2O2 + 2I- --> I2 + 2H2O. le diiode est en défaut ;[I2]fin= ½[I- ]départ =10-5 mol/L à tfin , A= e L [I2]fin= 2 105 * 1 * 10-5 = 2 ; à t½, At½ = 1. vitesse = 1/V dnI2/dt =d[I2] / dt si V est constant. d[I2] = 10-6 mol/L ; dt = 10 s doù v =10-6 / 10 = 10-7 mol L-1 s-1. HCOO- + HNO2= NO2- + HCOOH Qr,i=[NO2-]i[HCOOH]i / ([HNO2]i[HCOO-]i)= 1. car [NO2-]i=[HCOOH]i = [HNO2]i=[HCOO-]i= 500*0,02 /200 = 0,005 mol/L K=[NO2-]éq[HCOOH]éq / ([HNO2]éq[HCOO-]éq) 10-3,2 = [NO2-]éq[H3O+]éq / [HNO2]éqsoit [NO2-]éq /[HNO2]éq =10-3,2 /[H3O+]éq ; 10-3,8 = [HCOO-]éq [H3O+]éq / [HCOOH]éq soit [HCOOH]éq / [HCOO-]éq=[H3O+]éq /10-3,8 ; K=10-3,2 /10-3,8 = 100,6 = 4. Qr,i< K, donc évolution dans le sens direct. à pH=2,5 ( inférieure au pKa) la forme acide HNO2 prédomine surNO2-. HCOO- = NO2- + HNO2 = NO2- + HCOOH initial 50*0,02 = 1 mmol 1 mmol 1 mmol 1 mmol en cours 1-x 1-x 1+x 1+x final 1-1/3 = 2/3 1-1/3 = 2/3 1+1/3 = 4/3 1+1/3 = 4/3 6 mmol/L soit 6/5 = 1,2 mmol dans 0,2 L et 1+x = 1,2 soit x = 0,2 mmol. pH = ½(pKa1 + pKa2 ) = ½(3,2+3,8) = 3,5. retour - menu