|
suite --> charge d'un condensateur ( concours sage femme) (sans calculatrice) |
|||
|
|||
|
On prendra p² = 10 et racine carrée (0,1) = 0,32. On considère un pendule élastique horizontal constitué d'un solide S de centre d'inertie G et de masse m pouvant glisser sans frottements sur un support horizontal et d'un ressort à spires non jointives de constante de raideur k et de masse négligeable. Lorsque le solide est en équilibre son centre d'inertie est en O. Ecarté de sa position d'équilibre, il oscille autour de O suivant un axe horizontal Ox. La position du solide est repérée par l'abscisse x de G. 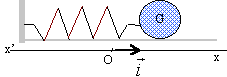 L'étude du mouvement se fait au moyen d'un ordinateur muni d'un capteur et d'une interface appropriée. L'enregistrement x=f(t) est donné ci-dessous. 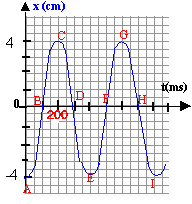
amplitude (lecture graphe) : 4 cm ou 0,04 m. si la valeur absolue de l'abscisse est égale à l'amplitude, alors la vitesse est nulle : points A, C, E, G, I. si l'abscisse est nulle alors la vitesse est maximale : points B, D, F, H. période
(lecture graphe) T0 = 0,4 s.
une force (newton) est une masse (kg) fois une accélération (m/s²) d'où k : [kg] [m] [s]-2 [m]-1 soit [kg] [s]-2 (masse / raideur) : [kg] [kg] -1[s]2 soit [s]2 racine carrée ( m/k) : [s] 2
p
est sans dimension: donc la relation
3
est correcte.
k = 4*10*0,2
/ 0,4² = 50
N/m.
Em=0,5 *50*0,04² = 0,04 J. au point D, l'énergie de l'oscillateur est sous forme cinétique Em= ½ mVm² en absence de frottement l'énergie mécanique se conserve. ½ mVm² = 0,04 soit Vm = racine carrée (0,08/0,2) =racine carrée (0,4) = 0,64 m/s.
en présence de frottement, l'amplitude diminue régulièrement ( amortissement)
retour - menu |