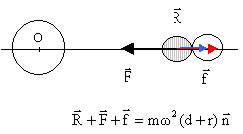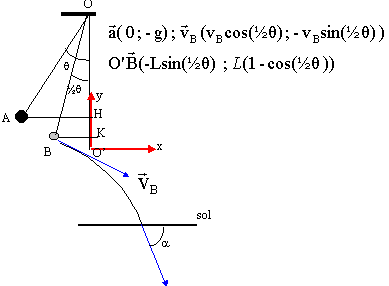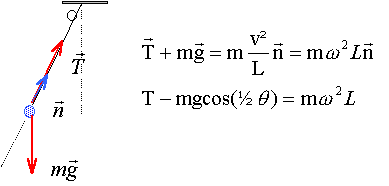|
concours d'entrée : technicien supérieur météo 01 |
|||
|
|||
|
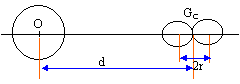
La comète Shoemaker-Levy est passer en juillet 92 suffisamment près de Jupiter pour se fragmenter en morceaux. Le but est de comprendre l'origine de cette fragmentation et d'estimer l'ordre de grandeur de la taille des morceaux issus de cette fragmentation. Le référentiel choisi est Jupiterocentrique, supposé galiléen. masse de Jupiter : MJ= 1,91 1027 kg ; rayon Jupiter : RJ= 71400 km ; masse volumique de Jupiter : mJ. G= 6,67 10-11 S.I. volume d'une sphère : 4/3 pr3 ; si e est petit devant 1 1/(1+e)2 = 1-2e.
mouvement circulaire uniforme : la seule force qui agit sur GC et la gravitation exercée par Jupiter accélération et force de gravitation sont centripètes GMJMC/d² = MCw²d w² = GMJ / d3.
F= GMJ m/(d-r)² gravitation exercée par Jupiter sur m f= Gm² / r² gravitation entre les deux sphères de masse m R action de contact entre les sphères n vecteur unitaire dirigé vers Jupiter. GMJ m/(d-r)² -Gm² / r² -R = mw²(d+r) d'une part : 1/(d-r)² = 1/(d²(1-r/d)²) = (1+2r/d)/d² d'autre part : mw²(d+r) = GMJ m(d+r) / d3. GMJ m(1+2r/d)/d²- f -GMJ m(d+r) / d3 = R GMJ m / d3 ( 3r) -f = R si le contact est rompu alors R est nulle et flim = GMJ m / d3lim ( 3r). flim = GMJ m / d3lim ( 3r)= Gm² / r² d3lim =MJ/m 12r3= mJ/mC 12RJ3 masse volumique de Jupiter = masse volume =1,971027/(4*3,14/3*(7,14107)3)= 1290 kg/m3. dlim
= racine cubique(12*1,29)*RJ
= 2,46RJ
.
F-f - R - FC = mw²(d+r) R + FC = F- mw²(d+r) -f rupture du contact : R=0 soit FC = F- mw²(d+r) -f = GMJ m / d30 ( 3r)-flim. FC /flim=d3lim / d30 -1 = (2,46/1,5)3-1 = 3,41.
|
|||
|
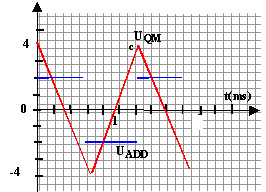
Inductance d'une bobine : 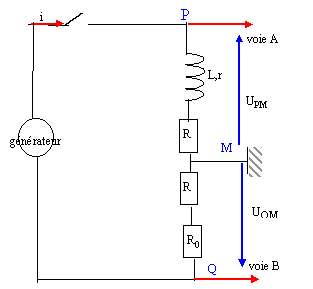 Le montage comporte monté en série : un générateur faisant circuler un courant variable i(t) ente P et Q, une bobine d'inductance L et de résistance r, deux conducteurs ohmiques de résistance R= 100 ohms et un rhéostat de résistance variable R0. L'oscilloscope utilisé comporte une touche ADD permettant, lorsqu'elle est actionnée, d'observer sur l'écran la tension notée UADD, somme des tensions reçues sur les voie A et B : UADD = UPM + UQM.
corrigé
UMQ= (R+R0)i soit UQM= - (R+R0)i UADD= (R+r)i + Ldi/dt -(R+R0)i = (r-R0) i + Ldi/dt si r = R0 alors UADD= Ldi/dt. UQMest une fonction affine par intervalle, sa dérivée est une fonction constante par intervalle. dUQM/dt = -(R+R0) di/dt soit di/dt =-1/(R+R0) dUQM/dt = -1/109 dUQM/dt UADD= Ldi/dt. est alors une fonction rectanglaire. d'après le graphe :dUQM/dt = 8 volts / (3*0,2 10-3)seconde = 13 333 Vs-1. soit di/dt = -13 333 /109 = -122,3As-1. sur le même intervalle UADD= -2V donc L= -2/ (-122,3) = 16,3 mH. période : 6 divisions soit 6*0,2 10-3 = 1,2 10-3 s. fréquence = 1/ 1,2 10-3 = 833,3 Hz.
|
|||
|
pendule simple : On considère un pendule simple de longueur L= 1m et de masse m=100 g. Il est écarté de sa position d'équilibre d'un angle q=30°. g =9,81 m/s². 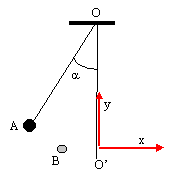
altitude de B : O'K= L(1-cos(½q)) altitude de A : O'H= L(1-cosq) travail du poids de A en B : mg(O'H-O'K) = mgL(cos(½q) - cosq) La tension du fil perpendiculaire à la vitesse ne travaille pas. en assimillant l'arc de cercle AB au segment AB de longueur L½q ( angle en radian) le travail des frottements f est : - f L½q écrire le théorème de l'énergie cinétique entre A et B, sachant que la vitesse en A est nulle : ½ mv²B = mgL(cos(½q) - cosq) -f L½q. en absence de frottement :v²B = 2gL((cos(½q) - cosq)) vB=
1,4 m/s.
remplacer par v² par : 2gL((cos(½q) - cosq)) et développer: T=
mg(3cos(½q)-2cosq)
= 1,14
N.
ce qui est écrit en gras et en bleu est un vecteur. (voir schéma ci-dessus) vitesse initiale vB(1,35 ; -0,362) accélération a(0,-g) position initiale O'B(-0,256 ; 0,034) la vitesse à la date t est une primitive de l'accélération : v(1,35 ; -9,8t -0,362) le vecteur position à la date t est une primitive de la vitesse : OM(x= 1,35t-0,256 ; y = -4,9t²-0,362t+0,034) éliminer le temps pour trouver l'équation de la trajectoire : t = (x+0,256) / 1,35 = 0,74 x +0,19 repport dans y : y = -2,68
x²-1,646x-0,212.
résoudre l'équation : -1 = -2,68 xI²-1,646xI-0,212. xI = 0,315 m. vitesse au sol vI : tI = 0,74 xI+0,19 = 0,423 s. repport dans l'expression du vecteur vitesse : vI ( 1,35 ; -9,8*0,423-0,362 = -4,51 ) vI² = 1,35² + 4,51² soit vI = 4,71 m/s. inclinaison de la vitesse par rapport à l'horizontale : tan a = 4,51 /1,35 = 3,34 a = 73°.
retour - menu |