|
|
|||
|
|||
|
rotation de la terre : gravitation terrestre : La terre tourne uniformèment autour de son axe, sa période de révolution est proche de 24 heures. La circonférence de la Terre est égale à 40 000 km. G= 6,7 10-11 S I ; 6,4*2p voisin de 40.
corrigé 1 et 2 sont vraies. 3 est faux : rayon terrestre RT= circonférence / 2p = 40 000 / 2p = 6,4 103 km l'altitude h vaut 12,8 103 km soit 2RT. gravitation au sol : g0 = GMT/R²T soit GMT =g0R²T gravitation à l'altitude h=2RT : g = GMT/(RT+h)² = GMT/(9R²T ) soit g =g0R²T/(9R²T ) =g0/9. 4 est vrai : accélération centripète aN= v²/ RT et 2p/C = 1/ RT. |
|||
|
donnée : 4p²=40.
corrigé 1 est faux : le mot uniforme signifie : norme du vecteur vitesse constante mais la direction du vecteur vitesse peut changer et alors il existe un vecteur accélération non nul.( exemple mouvement circulaire uniforme : l'accélération est centripète aN= v²/R). 2 est faux : si la norme de la vitesse reste constante le mouvement est uniforme. 3 est vrai 4 est faux : la vitesse de rotation étant constante, l'accélération tangentielle est nulle ; l'accélération centripète vaut v²/R. |
|||
|
Un enfant lance une balle de masse 100 g vers le ciel. La balle quite sa main à 1,5 m de hauteur au-dessus du sol avec une vitesse de 10 m/s. L'angle entre le vecteur vitesse à l'instant du lancer et l'horizontale est de 45°. On négligera les frottements. sin45 = cos 45 = 0,7 ; g= 10 m/s².
corrigé 1 est vrai ½mv² = 0,5*0,1*10² = 5 J 2 est faux : seule la composante verticale de la vitesse est nulle au sommet de la trajectoire. 3 est faux :
à quelle date la balle repasse-t-elle à l'altitude 1,5 m ? 1,5 = -5t² + 7t +1,5 0 = -5t² + 7t soit -5t +7=0 ou t = 1,4s. 4 est vrai théorème de l'énergie cinétique entre l'instant de départ et l'arrivée au sol : ½mv²-½ 10² = mgh ( travail moteur du poids : altitude finale inférieure à l'altitude initiale) v² = 10²+ 2gh . |
|||
|
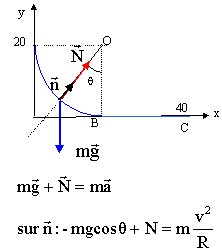
Le centre d'inertie d'un mobile S de masse m=500 g, lâché du point A sans vitesse initiale, glisse sur une piste ABC située dans un plan vertical. La partie AB est un quart de cercle de rayon R=20 cm. Les frottements sont négligés. La partie BC est horizontale. 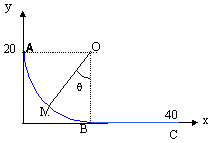
corrigé 1 est vrai : théorème de l'énergie cinétique entre A et B : ½mv²B-0 = mgR ( travail moteur du poids : altitude finale inférieure à l'altitude initiale) v² = 2gR = 2*10*0,2 = 4 soit vB=2m/s. 2 est faux : l'accélération normale est v²M/R; la masse ne doit pas intervenir dans l'expression de l'accélération. 3 est faux :
4 est vrai : un peu avant le point B, l'accélération est différente de zéro ( aN= v²B/R) après le passage en B le mouvement est rectiligne uniforme ( pas de frottements) donc l'accélération s'annule. |
|||
|
Une gouttelette d'huile, de masse m, portant une charge q négative, est en équilibre à mi distance entre les plaques d'un condensateur plan portées respectivement aux potentiels VA et VB. On suppose que dans la région de l'espace où se trouve la gouttelette, le champ est uniforme et a pour valeur E=105 V.m-1 .
corrigé La goutte est en équilibre sous l'action de son poids, vertical vers le bas, valeur mg et de la force électrique, verticale, vers le haut, valeur |q|E. La charge étant négative, le champ électrique est vertical, vers le bas ( colinéaire à la force électrique et de sens contraire) Le champ électrique pointe vers le plus petit potentiel, donc VB<VA et UAB <0 1 : vrai. La goutte d'huile pseudo -isolée est initialement sans vitesse quelle que soit sa position entre les plaques 2 : faux. champ (V/m)= tension(V) / distance des plaques (m) ; d= tension / champ = 1000/105 = 0,01 m = 1 cm.= 10 mm 3 : vrai. |q|E. = mg soit |q|= mg/E = 8 10-15*10/105=8 10-19 C soit 5e. 4 : faux. |
|||
|
Des noyaux d'hélium He2+ (ou particules a ), initialement au repos, sont accélérés par un champ électrique de valeur constante E= 2 105 V/m , et acquièrent une vitesse v0 = 107 m/s. g= 10 m/s² ; pour un noyau d'helium m/(2e)= 2,1 10-8 kg C-1 ; 2e/m = 0,5 108 kg-1 C ; 1 eV= 1,6 10-19 C
corrigé force électrique F= 2eE ; poids P=mg ; F/P= 2eE/(mg) = 2e/m 104 = 0,5 108104 =0,5 1012. le poids est négligeable devant la force électrique : 2 :vrai . La seconde loi de Newton s'écrit : 2eE=ma soit a = 2e/m E ; force électrique et accélération sont colinéaires et de même sens car 2e/m positif 1 :vrai . énergie cinétique : ½mv²0 = 0,5 *2,1 10-8*2*1,6 10-19*1014 J puis diviser par 1,6 10-19 pour passer des joules aux électronvolts. Ec= 2,1 106 eV= 2,1 MeV 3 :faux . Tous les isotopes de l’hélium n'ont pas la même masse (mais la même charge 2e) : l'énergie cinétique acquise est égal au travail de la force électrique ; ce dernier vaut W= 2e U, indépendant de la masse .4 :vrai . |
|||
|
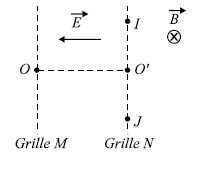
Un
électron est émis, sans vitesse initiale, au
point O, trou dans la grille M. Entre les deux grilles M et
N, règne un champ électrique E uniforme,
perpendiculaire aux plaques, dirigé de la grille N
vers la grille M. Au delà de la grille N,
règne un champ magnétique B uniforme dont la
direction est indiquée sur le schéma
ci-dessous. |UMN|= 100 V pour l'électron : m/e= 5,6 10-12 kg C-1 et
e/m = 1,8 1011 C kg-1. O'I=O'J distance entre les deux grille d= 1
m
corrigé L'électron est accéléré entre M et N et acquiért l'énergie cinétique ½mv² égal au travail moteur de la force électrique qE travail moteur de cette force : qUMN; q<0 ; W>0 donc UMN<0 1 : faux. Entre les grilles M et N, l’électron a un mouvement rectiligne uniformément accéléré .2 : faux
Le champ magnétique ne modifie pas la valeur de la vitesse. vitesse en O' : ½mv²= eU soit v²= 2eU/m= 2*1,8 1011*100 = 36 1012. v= 6 106 m/s.donc 4 vrai.
|
|||
|
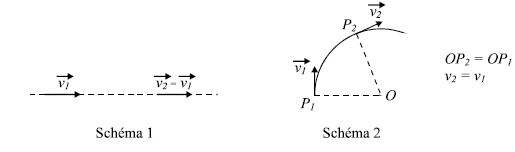
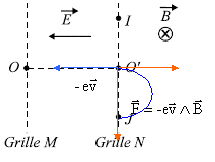
Les schémas ci-dessous représentent des portions de trajectoires de faisceaux d'électrons, lancés avec des vitesses de même valeur vi , dans un champ uniforme, soit électrique E soit magnétique B. On néglige l'effet des forces de pesanteur. Les vecteurs v1, v 2 , a1 et a2 représentent respectivement les vecteurs vitesses et accélérations des électrons aux instants t1 et t2.
corrigé 1 , 2 vrais : 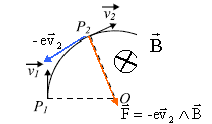
OP1 = r = mv/(eB)= 5,6 10-12 * 107 / 0,56 = 10-4 m 3 faux. la période est indépendante de la vitesse 4 faux. |
|||
|
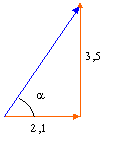
Un teslamètre est un appareil de mesure du champ magnétique. Le capteur est une sonde de Hall qui fournit une tension proportionnelle à la valeur de la composante du champ magnétique orthogonale à la surface de la sonde. Cette tension est ensuite amplifiée. Le coefficient de conversion de l'appareil utilisé est de 0,1V/mT. On utilise ce teslamètre pour étudier le champ magnétique terrestre. Tout d'abord on règle le zéro de la sonde, puis on l'oriente correctement afin de mesurer la composante horizontale du champ magnétique terrestre : la tension mesurée est de 2,1 mV . Ensuite la sonde est orientée pour mesurer la composante verticale du champ magnétique terrestre : la tension mesurée est alors de 3,5 mV. Données : • tan 60° = 1,73 ; cos 30° = 0,87 ; cos 60° = 0,50 • tan 30° = 0,58 ; sin 30° = 0,50 ;sin 60° = 0,87
corrigé 0,1 V = 100 mV correspond à 1 mT = 10-3 T soit 2,1 mV pour 2,1 10-5 T. 1 vrai.
direction du champ magnétique terrestre par rapport à l'horizontale : tan a = 3,5/2,1 =1,7 ; d'où a = 60 ° par rapport à l'horizontale 2 faux. tension mesurée : 3,5 / sin 60 = 4 mV donc 3 faux. 4 vrai. |
|||
|
Certaines pistes africaines présentent une succession régulière de bosses (tôle ondulée). Sur ces pistes, un véhicule subit des oscillations de très forte amplitude pouvant aller jusqu'à détériorer le véhicule. Ce phénomène est dû à l'entrée en résonance de l'oscillateur constitué par le véhicule, les ressorts de suspension et les amortisseurs. L'oscillateur peut être schématisé par un pendule constitué par un ressort de raideur k et par une masse m=1 t. La distance horizontale entre deux bosses successives est constante et vaut 2m. Le véhicule se déplace à vitesse constante de 36 km/h.
corrigé 1 est vrai : la piste constitue l'excitateur, l'oscillateur constitue le résonateur : à la résonance l'amplitude des oscillations est maximale. 2 est faux : à la résonance la fréquence de l'excitateur est égale à la fréquence propre du résonateur. vitesse : 36 km/h = 36/3,6 = 10 m/s longueur d'onde = distance entre deux bosses successives = 2 m fréquence excitateur = f0 =10/2 = 5Hz. 3, 4 sont vrais : f 0= 1/ (2p) racine carrée (k/m) soit en élevant au carré : k = 4p²f²0m k = 4*10*25*1000 =106 N/m. en modifiant la vitesse du véhicule on modifie la fréquence de l'excitateur. |
|||
|
On considère un pendule simple constitué par un solide de masse m= 100 g suspendu à l'extrémité d'un fil de longueur L=1m. Celui-ci est écarté de sa position d'équilibre d'un angle a0=8°, puis lâché sans vitesse initiale. Le plan horizontal contenant la position d'équilibre du solide est choisi comme plan de référence où l'énergie potentielle de pesanteur est nulle. cos 8=0,99 ; sin 8 = 0,14 ; racine carrée (20)=4,47 ; g= 10 m/s².
corrigé 1 est vrai : 2 est faux : Lorsque l'amplitude angulaire est maximale toute l'énergie mécanique est sous forme potentielle de pesanteur. Avec l'origine choisie E= mgL(1-cos 8) E= 0,1 *10*1(1-0,99) = 0,01 J. 3 , 4 sont vrais : au passage à la position d'équilibre, l'énergie est sous forme cinétique : ½mv²max. en absence de frottement l'énergie mécanique se conserve : 0,01 =½mv²max. v² max = 0,02/0,1 =0,2 = 20/100 soit vmax = 0,447 m/s. si ½mv² = 0,01/4 = 0,0025 J alors v² = 0,005/0,1 = 0,05 soir v² = 0,25 v² max et v = ½ vmax. |
|||
|
On considère un ressort de constante de raideur k, à l'extrémité duquel est accrochée une masse m. Lorsque l'on suspend une masse m=160g à l'extrémité libre du ressort celui-ci s'allonge de Dl=4 cm. ( g=10 m/s² p² =10)
corrigé 1 est vrai : à l'équilibre le poids et la tension (T= kDL)du ressort se neutralisent 2 est faux : poids = mg = 0,16*10 = 1,6 N puis k = 1,6 / 0,04 = 160/4 = 40 N/m 3 est faux : période = 2p racine carrée (m/k). 4 est faux : lorsque x(t) = 0,02 m ( amplitude), l'"nergie de l'ozcillateur est sous forme potentielle élastique : ½kx²max. E= 0,5 *40*0,02² = 20*4 10-4 = 8 10-3J = 8 mJ.
|
|||
|
Soit le circuit ci-dessous comprenant un générateur de tension idéal E= 10V, un interrupteur K, une bobine inductive (L=10mH; r = 10 W) et un résistor R=1 kW. A l'instant t=0 on ferme l'interrupteur K. 1/ 101 = 9,9 10-3 ; 1/110 = 9,1 10-3 ; 1/102 = 9,8 10-3. 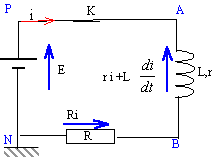
corrigé 1 est vrai : retard à l'établissement du courant dans un circuit inductif. 2 est vrai : la tension aux bornes de R est encore nulle (i voisin de zéro) la tension aux bornes de la bobine vaut 10 V. 3 est faux : la constante de temps est t ==L/(R+r) = 0,01 / 1010 = 9,9 10-6 s. inductance en henry et résistance en ohms. 4 est vrai : en régime permanent , l'intensité est constante ( donc di/dt =0) et rension aux bornes de la bobine vaut r I 10 = R I + r I soit I = 10 / (1000+10) = 10 / 1010 = 9,9 10-3A=9,9 mA.
|
|||
|
On considère le montage ci-dessous : 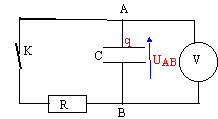 Le voltmètre a une résistance interne de 10 MW, soit pratiquement infinie, il indique une tension UAB = +9 V. La capacité du condensateur est C= 2,2 m F. R= 4,7 kW.
corrigé 1 est faux : si UAB = qA/ C est positive, C étant positive alors la charge de l'armature A est positive. 2 est faux : énergie stockée : E= ½CU²AB =0,5 * 2,210-6*9² = 89,1 10-6 J 3 est vrai : l'armature B est négative : lors de la décharge les électrons se déplacent de B vers A. Le sens conventionel du courant est de sens contraire. 4 est vrai : |
|||
|
On étudie les oscillations électriques libres d'un dipôle RLC série.
corrigé 1 est vrai : 2 est faux : l'énergie est dissipée dans les résistances et dans les conducteurs ( pas dans le condensateur supposé parfait) 3 est faux : l'amplitude des oscillations diminue et si R est assez grand on n'observe plus d'oscillations ( régime apériodique) 4 est vrai : période = 2p racine carrée (LC) si L et C doublent, le produit LC quadruple et racine carrée (LC) double ainsi que la période.
|
|||
|
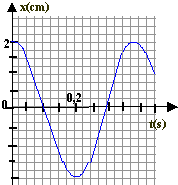
On étudie un dipôle RLC en régime sinusoïdale forcé. Un oscilloscope permet de mesurer les tensions u(t) aux bornes du générateur et uR(t) aux bornes de la résistance R.( R= 100 W) racine carrée (2) = 1,4 et 1/ racine carrée (2) = 0,7. 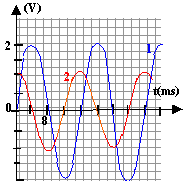
corrigé 1 est vrai : les courbes étant décalées, le circuit n'est pas à la résonance et l'impédance Z de ce dernier est supérieure à sa résistance R u(t) = Zi(t) et uR(t) = Ri(t) : la courbe de plus grande amplitude est u(t). 2 est vrai : amplitude de la tension uR(t) (lecture graphe) : 1 = R Imax = 100 Imax = 100 Ieff racine carrée (2) Ieff = 1 /(100*1,4) = 0,7 /100 = 7 10-3A = 7 mA. 3 est vrai : impédance Z = Umax / Imax avec Umax = 2V et Imax = 1/100 = 0,01A (lecture graphe) Z= 2 / 0,01 = 200 W. 4 est vrai : à la résonance Z=R or u(t) = Zi(t) et uR(t) = Ri(t) et les courbes ne sont pas décalées. retour - menu |
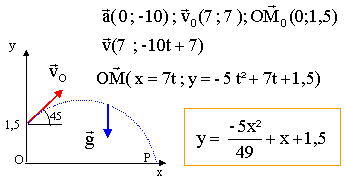

 donc
3 faux.
donc
3 faux.