|
satellite
-chute-oscillations électriques
EPF
02
durée
: 2h ; les exercices 1 et 2 sont obligatoires puis choisir 2
autres exercices
|
|
|
|
Satellites terrestres
:
On suppose que la terre a une répartition de masse
à symétrie sphérique de centre O. La
base de lancement de Kourou est située à
5° de latitude nord.
- Que pensez-vous des affirmations ou interrogations
suivantes ? Justifier rapidement votre choix.
a / Pour étudier le mouvement d'un satellite
autour de la terre, on peut négliger l'influence
du soleil et des autres planètes du système
solaire.
b / Un élève de terminale peut faire
l'étude du mouvement de ce satellite dans un
référentiel terrestre.
c / Un satellite géostationnaire n'est soumis
à aucune force.
d / Le choix de Kourou est dûau fait que le champ
de pesnteur y est plus faible.
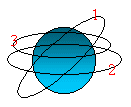
e / parmi les orbites ci-dessous, la ou lesquelles sont
possibles pour un satellite géostationnaire ?
- Calculer la vitesse angulaire d'un satellite
géostationnaire. Le résultat sera
donné avec trois chiffres significatifs.
masse de la terre : MT=5,98 1024 kg
; rayon terrestre : RT= 6370 km ; constante de
gravitation G= 6,67 10-11 m3
kg-1 s-2 ; période de
rotation de la terre sur elle même : T=23h56min ;
période de rotation de la terre autour du soleil :
T' =365,25 jours.
corrigé
|
vrai
|
Le champ de gravitation terrestre à
une altitude de 36000 km est bien supérieur
au champ de gravitation crée par le soleil
en ce point ; ce champ varie en raison inverse du
carré de la distance.
|
|
faux
|
l'étude est très commode dans
le référentiel
géocentrique
|
|
faux
|
le satellite géostationnaire est
soumis à la force de gravitation
terrestre
|
|
faux
|
Kourou est proche du plan
équatorial
|
|
orbite 2
|
un satellite géostationnaire se
trouve dans le plan équatorial
|
Le satellite géostationnaire a la même vitesse
de rotation que la terre.
T=
23*3600+56*60 = 86160 s
fréquence
: f = 1/86160 = 1,161 10-5 Hz
w=2
p f
=6,28*1,161 10-5 =7,288
10-5 rad/s.
|
|
chute libre avec vitesse
initiale :
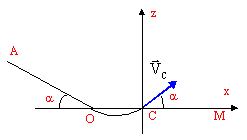
On abandonne sans vitesse initiale au point A un corps
assimilable à un point matériel de masse m. Il
glisse sans frottement sur la courbe AOC et arrive en C avec
une vitesse VC. La partie OC est une piste
circulaire de rayon R. Au delà du point C la masse
quitte la piste et retombe au point M sur le plan
horizontal. Les frottements sont négligés et
g= 9,8 S.I.
- Etablir l'équation horaire du mouvement sur le
plan incliné s=f(t). Exprimer la valeur
V0 de la vitesse au point O en fonction de
a, g, L=AO. Expliquer pourquoi
le module de la vitesse est le même en C qu'en
O.
- Etablir en fonction de a,
V0, g l'équation de la trajectoire du
mobile entre les points C et M dans le repère
précisé sur la figure. Donner l'expression
de la portée CM en fonction de a,
V0, g puis de L et a.
Calculer CM si L=1,6 m et a =
p/4.
corrigé
Sur le plan incliné, le solide est soumis à
son poids et à l'action normale du support. La
seconde loi de Newton s'écrit, sur un axe
parallèle au plan dirigé vers le bas : mg sin
a
= ma soit a = gsina.
la vitesse
est une primitive de l'accélération : v(t) =
gsina
t
la position
est une primitive de la vitesse : s(t) = ½gsina
t².
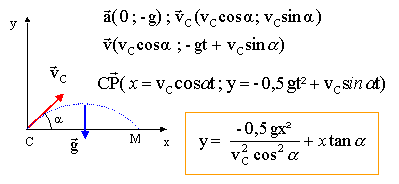
théorème de l'énergie cinétique
entre A et O : seul le poids travaille, l'action du support
étant perpendiculaire à la vitesse.
½mvO²
-0 = mgLsina.
vO²
= 2gLsina.
C est
à la même altitude que le point O: le travail
du poids ( force constante) ne dépend que de
l'altitude de départ et de l'altitude
d'arrivée. Donc la vitesse en C a même valeur
que la vitesse en O.
portée : yM=0
( -½g x
/ v²C cos a
)+sina)
x/cosa=0
x= 0
correspond au point C
xM=
2sina
cosa
v²C / g = sin
(2a)
v²C / g
.
or
v²C =2gLsina.
xM=
2 L
sina
sin (2a).
v²O
=2*9,8*1,6*sin45 = 22,17 soit vO
=4,7
m/s.
xM=
2 *1,6 sin45 *sin90 = 2,26
m.
|
|
chute avec
frottements :
On se propose d'étudier la chute, sans
vitesse initiale, d'une petite bille d'acier de rayon R et
da masse volumique r dans un
liquide visqueux de masse volumique r
1, la glycérine. On admet que la
bille, dont le centre est animé d'un mouvement de
vitesse v est soumise à :
- son poids P= mg ;
- la poussée d'Archimède A=
r 1 Vg dirigée de bas en haut, V
reprèsentant le volume de la sphère de rayon
R.
- la résistance au mouvement F= 6pRhv
(h étant la
viscosité du fluide).
La bille est lâchée sans vitesse initiale
dans le fluide.
- Etablir l'expression liant v(t) à sa
dérivée par rapport au temps. Montrer que
cette équation peut se mettre sous la forme dv/dt
+ v/t = C
- Préciser les expressions et unités de C
et t.
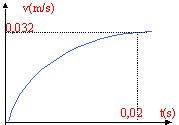
- L'expérience est réalisée et le
graphe v(t) est donné ci-dessous. En
déduire la vitesse limite de la bille.
Déduire des questions 1 et 2 la viscosité
de la glycérine.
R= 1,5 10-3 m ; g= 10 m/s² ; r
= 7800 kg m-3 ; r
1 = 1260 kg m-3 ; V= 4/3
p R3.
corrigé
poids vertical vers le bas : mg
poussée
d'Archimède, verticale vers le haut :
r1Vg
frottement,
verticale vers le haut : 6pRh
v
la seconde
loi de Newton s'écrit, sur un axe vertical
orienté vers le bas :
mg -
r1Vg
-6pRh
v = ma = m dv/dt
division par
m : g - r1Vg
/m = 6pRh
/ m v + dv/dt
Or V/m = 1/
r
; m = 4/3p
R3r
; p
R/m = 3/
(4R²r)
g (1-
r1/
r
) = 4,5h
/(R²r)
v + dv/dt
C= g (1-
r1/
r
) s'exprime en m/s²
1/t
= 4,5h
/(R²r)
; t
= R²r
/ (4,5h
) s'exprime en s.
vitesse limite vL= 0,032 m/s.
lorsque la
vitesse limite est atteinte, le mouvement est rectiligne
uniforme: dvL/dt=0
l'équation
différentielle s'écrit : C= vL/
t
soit t
= vL/ C
C=
9,8(1-1260/7800) =8,2 m/s² ;
t
= 0,032 / 8,2 = 3,9 10-3 s.
h
= R²r/
(4,5t)
= (1,5 10-3)² *7800 / (4,5*3,9
10-3) = 1 kg m-1
s-1.
|
|
QCM mécanique
: pas de justification pour les questions 1 et 2 ;
justifier pour la question 3.
- A la surface de la lune, le champ de
gravitation est environ 6 fois plus faible que lcelui
existant à la surface de la terre. Lors des
missions Apollo, un astronaute de masse 90 kg sur terre
avait à la surface de la Lune une masse de :
a/ 1,5 kg
b/ 540 kg
c/90 kg
- Dans le cas d'un mouvement circulaire uniforme :
a/ Le vecteur vitesse est constant.
b/ La valeur du vecteur vitesse est constante;
c/ La valeur du vecteur accélération est
nulle.
d/ Le vecteur accélération est nul ;
e/ La valeur du vecteur accélération est
constante;
f/ Le vecteur accélération est
constant.
- a/ Si une particule, initialement immobile, est
soumise à une force constante, sa trajectoire est
alors une droite.
b/ Si une particule est soumise à une date t>0
à une force constante, sa trajectoire
dépend des conditions initiales.
c/ Un satellite ayant une orbite circulaire autour de la
terre est soumis à une force constante..
corrigé
|
1c : vrai
|
la masse est constante (90 kg) c'est le
poids qui varie suivant le lieu.
|
|
2b : vrai
|
mouvement uniforme signifie : la valeur du
vecteur vitesse est constante
|
|
2e : vrai
|
accélération
centripète ( dirigée vers le centre
du cercle)
valeur aN=v²/R si v=Cte alors
aN=Cte.
|
|
3a : vrai
|
le vecteur accélération et le
vecteur vitesse sont colinéaires : donc
trajectoire rectiligne
|
|
3b : vrai
|
si la vitesse initiale et la force
constante sont colinéaires : mouvement
rectiligne
si la vitesse initiale et la force constante ont
des directions différentes : trajectoire =
arc de parabole
|
|
3c : faux
|
le satellite est soumis à la force
de gravitation centripète, de valeur
constante mais de direction variable (radiale :
dirigée suivant un rayon du cercle)
|
|
|
oscillations électriques
amorties :
On considère le circuit ci-dessous. l'interrupteur
1 est fermé, l'interrupteur 2 est ouvert. On ouvre
l'interrupteur 1 et on ferme l'interrupteur 2. On constate
sur l'écran d'un oscilloscope que u(t) est une
sinusoïde amortie.
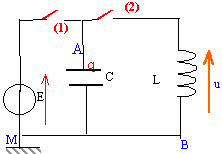
- Interprèter ce fait.
- Le logiciel d'acquisition mesure les valeurs des
amplitudes Un des oscillations pour chaque
période et nous propose, afin de déterminer
la loi d'évolution de cette amplitude en fonction
du nombre de périodes, les calculs suivants :
lnUn ; 1/Un ; Un ².
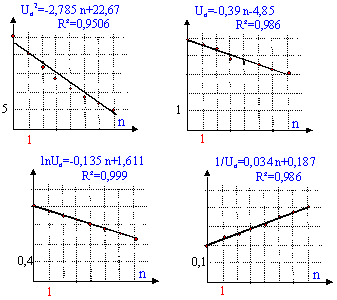
Ce logiciel fourni également la
représentation graphique de lnUn ;
1/Un ; Un ² en fonction du
nombre n de périodes écoulées, ainsi
que l'équation de la meilleur droite passant par
ces points . Le coefficient R² est d'autant plus
proche de 1 que la droite ajuste au mieux l'ensemble des
points
- Parmi les différentes possibilités,
quelle représentation paraît la mieux
adaptée.
- En déduire l'expression de Un en
fonction de n.
- Au bout de combien de pseudo-périodes
l'amplitude des oscillations est-elle divisée par
100.
|
n
|
Un
|
lnUn
|
1/Un
|
Un ²
|
|
0
|
5
|
1,61
|
0,2
|
25
|
|
1
|
4,5
|
1,5
|
0,22
|
20,25
|
|
2
|
4
|
1,39
|
0,25
|
16
|
|
3
|
3,5
|
1,25
|
0,29
|
12,25
|
|
4
|
3,2
|
1,16
|
0,31
|
10,24
|
|
5
|
2,85
|
1,05
|
0,35
|
8,12
|
|
6
|
2,55
|
0,94
|
0,39
|
6,5
|
|
7
|
2,25
|
0,81
|
0,44
|
5,06
|
corrigé
amortissement : perte d'énergie ( sous forme d'effet
joule dans la résistance du circuit) lors des
échanges d'énergie entre condensateur et
bobine.
La
représentation graphique la plus adaptée
correspond à R² le plus proche de1.
ln
Un= -0,1135n+1,61
si n=0 : ln
U0 = 1,61 soit U0 = 5V
ln
Un = -0,1135 n+1,61 = ln 0,05 = -2,996
0,1135 n =
2,996+1,61 = 4,606
n = 4,606 /
0,1135 proche de 41.
retour
- menu
|