|
aide
technique
2002
|
|||
|
|||
|
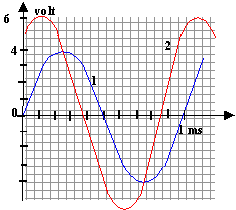
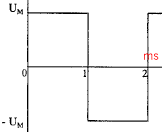
circuit RL : On applique aux bornes d'un circuit RL une tension sinusoïdale u (t)= Um sin(2pNt). On souhaite observer sur un oscilloscope la tension u(t) sur la voie Y1 et la tension v(t) aux bornes de R sur la voie Y2. Par ailleurs on veut insérer un ampèremètre dans le circuit afin de mesurer l'intensité efficace du courant.
corrigé 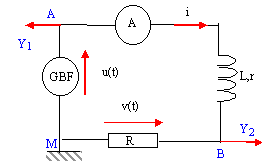
v(t) = R i (t) u(t) = uAB + v(t) Dans un circuit inductif la tension aux bornes du GBF est en avance sur l'intensité : la courbe 2, en avance sur la courbe 1, correspond à u(t). une période T correspond à 10 divisions, le déphasage correspond à environ 1,2 division soit 0,12 T. une période correspond à 360° donc j =360*0,12 = 43°. sur la courbe 1 on lit l'amplitude de la tension v(t) : environ 4 V la valeur efficace de v(t) vaut : 4 / 1,414 = 2,83 V. d'où Ieff = 2,83 / 1000 = 2,83 mA valeur
cohérente avec la valeur lue : l'écart
étant seulement de (3-2,83) / 3 = 0,04 ( 4 %)
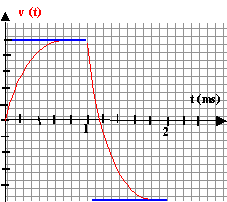
soit Z l'impédance du dipole RL série : d'une part Z = Ueff / Ieff = ( 6 / 1,414) / 3 10-3 = 1414 W. d'autre part Z² = R² + (Lw)² avec w = 2pf = 6,28 103 rad/s. période (lecture graphe : 10-3 s ) donc f = 1000 Hz 1414² - 1000² = (Lw)² = 106. Lw = 103 d'où L = 0,159 H. la constante de temps du circuit vaut : t = L/ R = 0,15 /1000 = 1,5 10-4s. Le régime permanent est atteint au bout d'une durée voisine de 5 t soit environ 8 10-4 s. pendant cette durée la bobine stocke de l'énergie et s'oppose à l'établissement du courant.
|
|||
|
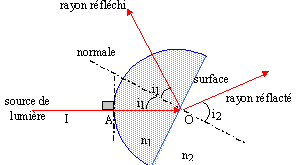
réfraction : Données : n1 =1,5 ; n2 = 1 ; i1 =30° On désire étudier la réfraction d'un faisceau de lumière blanche entre le plexiglas d'indice n1 et l'air d'indice n2. On utilise pour cela un demi-cylindre de plexiglas. 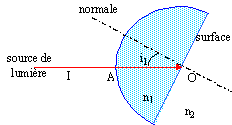
corrigé En A le rayon lumineux est perpendiculaire à la surface de séparation des deux milieux : l'angle dincidence est nul et en conséquence l'angle de réfraction r est nul( sin 0 = n sin r entraîne sin r = 0 soit r = 0). n sin i1 = sin i2 ; sin i2 = 1,5 sin 30 = 0,75 soit i2 = 48,6°.
réflexion totale : Quelle est la valeur maximale de i1 telle que le rayon réfracté n'existe plus ? |sin i2 | inférieur ou égal à 1 soit n |sin i1c| <=1 |sin
i1c| <= 1/n soit |sin i1c| <=
0,666 soit i1c <= 41,8°.
Dans le cas d'un laser : utiliser une cuve parallélépipédique remplie d'eau salée et légérement colorée ( rose violet) par une solution de permanganate de potassium : le trajet de la lumière laser réfractée est ansi matérialisée à travers le liquide. La source laser est placée au dessus de la surface du liquide.
|
|||
|
Mesure d'une longueur d'onde : On désire mesurer la longueur d'onde l d'une onde sonore. On réalise le dispositif schématisé ci-dessous : 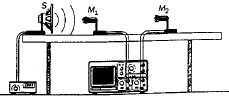 Le haut parleur émet une onde sonore reçue par les deux microphones. Les signaux détectés par ces microphones sont observés sur un oscilloscope bicourbe.
corrigé Un son de fréquence 15 000 Hz est aigu. Déplacer le micro M2 en laissant le micro M1 fixe par exemple. Lorsque la distance M1M2 est un multiple de la longueur d'onde de l'onde sonore, les deux sinusoïdes observées sur l'oscilloscope sont en phase ( non décalées). La plus petite distance conduisant à deux sinusoïdes en phase donne la longueur d'onde. La célérité des ondes sonores dans l'air est voisine de 340 m/s soit 340*3,6 = 1224 km/h. la longuer d'onde (m) est égale à la célérité (m/s) divisée par la fréquence (Hz) l = 340 / 15000 = 2,26 cm.
retour - menu |